Математическая модель струи

Автор уже рассматривал математическую модель струи на основе уравнений гравитомагнетизма [3]. Ниже предлагается другая модель, основанная на использовании сил Кориолиса. Возможно, что эти модели удастся объединить, но здесь не делается таких попыток и не выполняется какое-либо сопоставление прежней и новой моделей.

В [3] указано, что эксперименты позволяют установить только то, что вихрь образуется, когда скорость потока превышает некоторое пороговое значение [1]. Другое явление, наблюдаемое при вытекании воды из трубы, состоит в том, что сжавшаяся у выхода из трубы вода сравнительно быстро опять расширяется [2]. Однако ниже мы будем рассматривать струю, сохраняющую свою форму на большом расстоянии.

Такая струя создается в станках для «гидроабразивная резки – обработки материалов резанием, где в качестве режущего инструмента вместо резца используется струя воды или суспензия абразивного материала в воде, испускаемая с высокой скоростью и под высоким давлением» [4] – см. рис. 1. Этот метод применим для резки высокотвердых и хрупких материалов с высокими точностью, безопасностью и эффективностью.

Вода под давлением проходит через отверстие режущей головки, которая представляет собой алмаз, рубин или сапфир с отверстием меньше, чем острие булавки. По мере прохождения воды ее давление и скорость радикально увеличиваются до более чем 6.2 • 10⁸^ и 1000 м/сек [5]. Интересно отметить, что абразивные частицы добавляются в воду после того, как она приобрела высокую скорость под высоким давлением - см. рис.1.

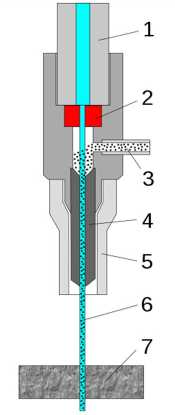
Рис. 1.

Схема установки гидроабразивной резки.

• 1    — подвод воды под высоким давлением,

• 2    — сопло,

• 3    — подача абразива,

• 4    — смеситель,

• 5    — кожух,

• 6    — режущая струя,

• 7    — разрезаемый материал.

2.    Уравнения гидродинамики для струи

Из этих замечаний следует, что мощность струи увеличивается постепенно и превышает мощность мотора на входе струи . Разработчики этого высококлассного метода почему-то не обращают на это внимание. Все кажется очевидным: «в природе подобный процесс, протекающий естественным образом, называется водной эрозией [4]». Далее в результате моделирования буде показано, что работа струи – это работа сил Кориолиса. Весьма живучим является мнение о фиктивности этих сил. Однако недавно появилось математически обоснованное доказательство физического существования этих сил [6, 7] и примеры конструкций [8], существование которых необъяснимо в отсутствии физических сил Кориолиса.

Для описания струи следует использовать гидродинамику. Уравнения гидродинамики для вязкой несжимаемой жидкости имеют следующий вид [9]:

div(v) = 0 ,                                       (1)

P ^t + ^P - jAv + P(v ' ^)^v - PF = 0 ,        (2)

где

• p = const - постоянная плотность,

• /J. - коэффициент внутреннего трения,

• р - неизвестное давление,

• v = [v_x, v_y, v_z] - неизвестная скорость, вектор,

F = [F_x, F y , F_z] - известная массовая сила, вектор, X, y,z,t - пространственные координаты и время. В этих уравнениях неизвестны р, v .

Если система является замкнутой, то система уравнений (1, 2) в стационарном режиме принимает вид [9]:

div(v) = 0,                                          (3)

• -J- Av + VD — p - F = 0,                     (4)

где неизвестны D, v. Уравнение (4) решается методом, предложенным [9]. При этом решение всегда существует и является единственным. После решения уравнения (4) определяются скорости и величина D, а давление вычисляется по уравнению вида р = — ^(W2) (кг^м-^сек-2),                      (5)

где

W² = (v² + v² + v²). (6)

В (5) слева – давление, а справа плотность кинетической энергии течения . Интеграл плотности по объему определяет энергию в объеме струи (кг·м²·c^-2=джоуль).

Если система абсолютно замкнута (например, в безбрежном океане или просто при достаточно большом максимальном радиусе), то выполняется условие VD ~ 0 . Таким образом, для замкнутой системы выполняются уравнение вида

J - Av + p - F = 0. (7) и определяется плотность энергии (5). Метод расчета таков, что не требует знания граничных условий – точность расчета тем больше, чем больше область интегрирования. В сущности, границы области существования течения определяются данными массовыми силами.

В нашем случае силы Кориолиса неизвестны, т.к. зависят от скоростей. Поэтому приходится выполнять расчет в в каком-нибудь дополнительном предположения. Мы будем предполагать, что границы струи (ее радиус) известны и продольная скорость на границе струи известна.

Струю удобно рассматривать в системе цилиндрических координат Г, ф, Z. В ней наблюдаются скорости массовых частиц vr, Уф, vz, направленные по радиусу, вдоль окружности и вдоль центральной оси. Скорости v^ соответствует угловая скорость

Ы = Уф/г.(8)

При наличии угловой скорости Ш возникают силы Кориолиса

Fr = 2pwvz,( 9)

Fz = 2рыиг,(10)

направленные вдоль радиуса и вдоль центральной оси соответственно. Уравнение гидродинамики в этом случае имею вид р • Avr + 2pvzM = 0,

F • ДVф + Fp = 0, р • Дvz + 2ршиг = 0, где Fp — неизвестная функция и движении:

(Fz + Fr + pg)dt = —р ^dvr + dvz +^y d^J,

Г AvJ		\ д 2 vr 1 д 2 vr д2vr " / дг2 г 2 дф 2 dz 2
д "=В1=	e	+ J дг 2	+	г 2 дф 2     dz 2	,         (14)
Д v z	le	, A d 2 vz + Г J ТГ J дг2	+	1 д 2 vz д2vz г 2 дф 2 дz 2 -

Силы Кориолиса приносят в систему импульс и энергию. Запишем уравнение закона сохранения импульса при таком где слева записан импульс, добавленный действующими силами за время dt, а справа изменение импульса кольца за это же время. Очевидно, dt = *

V z

Из (9, 10, 15, 16) получим:

(2шуг + 2mvz + g)dz = —vz ^dvr + dvz + 1dvpJ или

(2^vr + 2^VZ +g) = -Vz№ + ^ + 1^).(18)

'          ^z j ^z \dz dz 2 dz J

Таким образом, наличие угловой скорости W, т.е. вращение вихря следует из законf сохранения импульса .

Мы будем искать решение системы уравнений (4, 5, 6) в виде: vr = bro(r) + br(r) • exp(a p + /z), uv = bv(r)(20)

Vz = bz(r) • exp(K y + xz},(21)

где к,/ - некоторые константы, а b(r) — неизвестные функции аргумента Г. Тогда уравнения (11, 12, 13) после сокращения на общие множители примут вид:

(г + Г)1Г? + ^Ьг+Х2Ьг + 2PinvPbz^ = 0,

(r+ r)^^ + ^b^ + /2bv + FV(r^ = °'

(r + r)l^ + ^bz +X2bz + 2PinvPbr^ = 0,

2pbrob-^-pg = °.(25)

где

Pinv = 1/P-(26)

Из (8, 25) находим:

bro = g/(2").

Из (23) следует, что

^ = °-(28)

Из (28, 18) находим:

(2wVr + 2uVz) = -Vz (^ + 5) - g.(29)

Из (29, 19, 21) находим:

2u(br + bz) = -bz/(br + bz)- g(30)

^ = -°.5(bz/ + g/(br + bz)).(31)

Из (31, 20, 8) находим:

bv = -r- (bz/ + g/(br + bz)),(32)

Из (22, 24, 8, 32) следуют два уравнения

(^ + г)^ + К^+X2bz + 2PinvPbrby = °,(

(r + r)lr? + ^br+ X2br + 2PinvPbzbv = °.(34)

Одним из решений этой системы уравнений может быть:

br = bz,(35)

^ + r)12;bF + ^bz+x2bz + 2MinvPbzb^ = 0.

Итак, решение сводится к решению уравнений (36, 32), после чего можно найти все остальные функции.

Определим еще плотность потока энергии вдоль струи:

sz = FZVZ(37)

или

Sz = 2pMV^ = 2 pwb% exp2 (/z),(38)

Отсюда следует, что при / > 0 поток энергии увеличивается по мере движения струи , что является следствием работы сил Кориолиса, которые постоянно добавляют энергию в струю. Мощность, переносимая всей струей, при exp² (/z) ~ 1 равна

S = /J* 2pa)b' Z • 2яг • dr = 4ря f J ^b²r • dr. (39)

Наконец, найдем давление внутри струи по (5, 6):

p = - 2 (^2b2+b v ).                          (40)

Это давление превращает струю в твердое тело и удерживает жидкость в объеме струи.

Пример 1.

Рассмотрим условия одного процесса из [4]. «Вода, сжатая одним из основных компонентов системы - насосом высокого давления (4000 бар), проходит через водяное сопло, образующее струю диаметром 0.35 мм, попадающую в смесительную камеру. В смесительной камере происходит смешивание воды с абразивом (гранитным песком) и далее она проходит через второе, твердосплавное или алмазное сопло с внутренним диаметром 1 мм. Из этого сопла струя воды с абразивом выходит со скоростью около 1000 м/сек и попадает на поверхность разрезаемого материала.»

На рис. 2 показаны результаты расчета в системе СИ при:

R = 0.001, v_z = v_r = 1000 .

d ² b_z d²b_z

Показаны —₂ , —₂ , b_z = b_z, Ы, F_z = F_r, F ^ как функции радиуса r . Суммарная мощность, переносимая всей струей,

S = 1.6 • 10⁷ Wt .

Наконец, давление внутри струи p = 109 N/м2.

Пример 2.

Пример 1 рассчитывался для воды, у которой р = 1000, р = 0.0009 . Для воды с абразивом будем полагать, что плотность увеличилась до р = 5000, а коэффициент внутреннего трения не остался равным р = 0.0009 . В этом случае находим:

5 = 8.5 • 107 Wt,    р = 5 • 109 N/м2.

Пример 3.

Рассмотрим для сравнения струю воздуха, у которого р = 1.3, р = 1.5 • 10^-5 . В этом случае находим:

5 = 2.1 • 104 Wt,    р = 1.3 • 106 N/м2.

Пример 4.

Рассмотрим, наконец, струю воздуха с абразивом, приняв для нее р = 5000, р = 1.5 • 10^-5 . В этом случае находим:

5 = 3.6 • 109 Wt,    р = 5 • 109 N/м2.

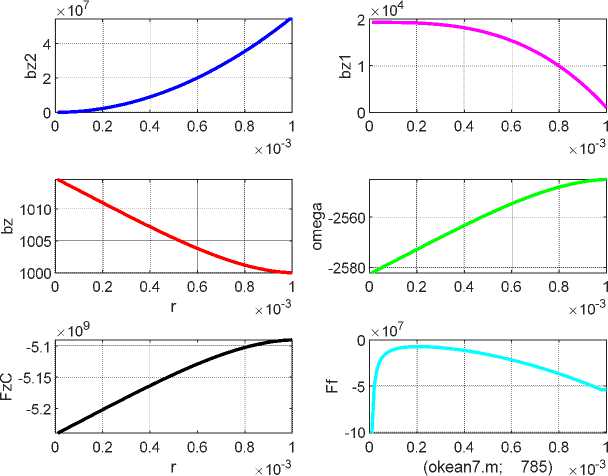
Рис. 2.