Математическая модель тепловых процессов и методика исследования теплоотдачи в пористом цилиндре

Пористые тела позволяют интенсифицировать теплоотдачу в элементах энергетических систем. Однако, большое разнообразие геометрии и сложность описания протекающих в пористых структурах процессов явились причиной того, что имеющиеся данные по теплоотдаче и сопротивлению пористых сред значительно отличаются друг от друга [1-3]. Поэтому изучение теплогидродинамических характеристик пористых материалов продолжает оставаться актуальным.

Исследование теплогидравлических характеристик пористого тела предполагает наличие адекватной математической модели протекающих в нем процессов. В известных моделях принят ряд грубых допущений. Например, считается, что температура теплоносителя совпадает с температурой каркаса (однотемпературная модель) [4]; некоторые модели не учитывают продольную теплопроводность каркаса [5] и др. Нет единого мнения о величине доли теплоты ^ q , воспринимаемой каркасом: одни принимают ^ q = 1 , т.е., что вся теплота от стенки передаются каркасу [5],

другие, пытаясь учесть отличие ^ q от 1, принимают предположение о не нулевом градиенте температуры на теплоизолированной стенке [6].

Дополнительной причиной расхождений экспериментальных данных по теплоотдаче и сопротивлению пористых структур является разный подход к описанию их характеристик. Так, в одних работах в качестве определяющего размера берется эквивалентный диаметр каналов, в других – средний размер пор, в некоторых – диаметр канала, в котором расположена пористая вставка и др. [7].

Новый подход к описанию геометрических и теплофизических свойств пористых материалов сделан в работе [8], где предложена геометрическая модель высокопористого ячеистого материала (ВПЯМ). Модель характеризует пористый материал большим чем ранее набором параметров, а именно: объемной пористостью 8 _v , просветностью 8 s , диаметром сферических пор d _сф , межцентровым расстоянием между сферическими порами l , эквивалентным диаметром каналов d _э , эквивалентным диаметром перемычек каркаса d _ск , удельной поверхностью пористости f _w , относительной площадью поперечного сечения каркаса 8 _ск и др. Относительные эффективные теплопроводности каркаса и теплоносителя предложено вычислять по формулам, которые удовлетворительно согласуются с литературными данными [8]:

Х ск = ^X к / X w = ⁸ _СК ; X f ^,эф = \эф/ X f = ^{1 -8} ск ;

• ⁸ ск = ^{(1 -8} v )/ ( 3 ^{- 2} d ск ) ’

где X w и X f — теплопроводности материала каркаса и теплоносителя, Вт/(мК); d ск = d _ск Jd _сф .

Объемные теплоемкости каркаса и теплоносителя приняты пропорциональными S v и ( 1 - S v ) , соответственно.

Целью выполненных исследований являлось:

• -    решение сопряженной стационарной задачи теплообмена пористого цилиндра с охлаждающим его однофазным теплоносителем;

• -    разработка методики исследования теплоотдачи в пористом цилиндре на основе полученного решения указанной сопряженной задачи;

• -    проверка методики исследования теплоотдачи на модельной задаче.

СОПРЯЖЕННАЯ СТАЦИОНАРНАЯ ЗАДАЧА ТЕПЛООБМЕНА ПОРИСТОГО ЦИЛИНДРА С ТЕПЛОНОСИТЕЛЕМ

Рассматривается пористое тело цилиндрической формы радиусом R и длиной l _ц (рис. 1). Боковая поверхность тела нагрета до температуры t _ст , которая может изменяться по длине цилиндра, не изменяясь во времени. В осевом направлении через пористое тело течет стационарный однофазный поток холодного теплоносителя массовым расходом G _f и начальной температурой t _f,0 . При течении сквозь пористое тело теплоноситель нагревается, а каркас охлаждается, в результате чего температуры каркаса t _ск и теплоносителя t _f изменяются как в продольном, так и в поперечном направлениях. Коэффициент теплоотдачи внутренней поверхности пористой структуры составляет a w , на входе и выходе потока - « о и a 1 , соответственно. Требуется рассчитать тепловую нагрузку, воспринимаемую теплоносителем, и температурные поля в каркасе и теплоносителе.

При стационарных режимах течения и нагревания процесс передачи теплоты от пористого тела к теплоносителю описывается сопряженной стационарной задачей теплообмена, включающей в себя краевые задачи теплопроводности каркаса и теплоносителя. В относительных переменных задачи имеют вид

L 2 5 L,56_CJ 5² 6_СК ск           ск

1 X I +

X 5X (  5X )5

⁺ a о ^(б f

-6_СК ) = 0 ск

(о < X < 1, о < Y < 1);(1)

56„ (0, Y) _ 0 5X’

6 ск ( 1, Y ) = f ( Y ) ;

^{56ск (} X ^,0) = Bi₀ [ 6_СК ( X ,0)-6_f0 ];

5Y            0 скf,0

■"■'Х" = Bl,[6, (X ,1МсК (X ,1)] ;(5)

56 _f _ b 5

5 Y ” X 5 X

56 f ( 0, Y ) _ ₀

5 X

f Y ) _ ( 1 -n Q ) Nu- [ е ст ( Y ) -6 f ( 1, Y ) ] ; (8) 5 X

6 f ( X,0)_6_№ _-1 ;          (9)

Здесь X _ rjR ; Y ^_ yjl ц ; U^-it ^- t „,„„ )/ t* ; L _ l „/ R ; a „ S . a , f „ l 2 /X„ ; b , = Nu f „ l „ /(s , Pe ) ; b _ 2 ( 1 -s„ L ( S v Pe ) ; Bi _a „ l Ц X _ck ; Bi . _a . l Ц X ^,,

^X ск ^{_ s} ck ^x w ; ^{Nu _ a} w RI ^X f,эф ; Pe _ w f DI a f ;

wf _ Gf /(pf SsПR2 ) - скорость фильтрации теплоносителя, м/с; t _ tст,Шах - tf,0 ; tст,тах – максимальная температура стенки, К;

af _ Xf Дрf cp ) - температуропроводность теп лоносителя, м2/с; D _ 2R - диаметр трубы, м.

Решение краевых задач (1)-(5) и (6)-(9) осу- ществляется с помощью конечных интегральных преобразований Фурье-Ханкеля [9, 10]:

6 ck,l ( ц n , Y m ) _ f ^/ 0 ( 4 n X ) f K y ( Y m Y ) 6 с_к ( X , Y ) dY - dX ,

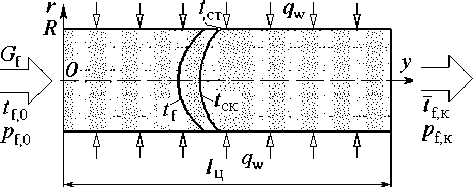
Рис. 1. Нагревание теплоносителя в пористом материале

е_t L ( 4 1 , Y ) _ f X/ 0 ( 5 i X ) 6 f ( X , Y ) dX .    (10)

Bi

Здесь K y ⁽Y m^Y ) ^{_ cos(}Y m^Y ) ⁺    "sin ⁽Y m^Y ) ,

Y m

Ц _n , Y _m и 5 1 - корни характеристических уравнений:

/ 0 (ц n ) _ 0 ;

t g ⁽Y m ) ¹

I

Bl Bl )

Y m Y m )

Bi o + Bi i

Y _m   Y _m

(1 -8 Q )Nu. J0 (; 1 )=S J^ 1);

J o ( с ) и J i ( с ) — функции Бесселя первого рода нулевого и первого порядков.

Дифференциальные уравнения (1) и (6) в преобразованиях (10) принимают вид:

⁹ к ⁽ц n , Y m ) = ¹

^z n , m

k d

Bi o 9 f,o + ( ц n L ) ² Z d p F p (y m ,1 ) p = 0

J 1U) ₊

Ц n

+ BiiKy (ym )ZASx,n, 19f,L (; 1,1) + a0 ZASxnn, 1Fm, 1 (Ym, S 1 )Ь I=0

^d 9 f, L + dY

k _d

9,e f,L = b 2 J 0 ( ; 1 ) Z d p Y p + p = 0

”            ”         Z             Z(12)

+ b 0 Z AnS x, n , I Z AmK y (Y mY )9 ск, L (Ц т , Y m ) n = 0

где   ^z n , m = a 0 ^{+ (} ц n^{L ) 2 +} y m ;     ⁹ 1 = b 0 + b i ^; 2 ;

S x, n , I = i XJ 0 ( ц n X ) J 0 ( ; X ) dX = ^{ц nJ 1} ^ ⁿ ) ^J 0^{L 1} ) 0                                       ^ц n S 1

F 1,p ( y m , Y ) = i z K ( y m Z 'dz =

F, ⁽y m Y ) + B 0 Am

= Y p F , ( y m i ) + [ K y ( Y m i ) " 1p Y m

уp_F,     ,   ^Y p ^{- 1 K} у ⁽ Y m ^{Y ) - (} pF . 2 ⁽ Y m , ^Y )

^{1 1} 6 V/ m¹ ) ^{+ p}                   2

Y2m приp = 0, приp = 1, приp >1;

• ^b 2 = b ^{( 1 -} n Q ) Nu ;

F f.„, ( y m ,; , ) = i K у ( y m i ) e f,L ( ; ,Y )di.

Решение обыкновенного дифференциального уравнения (12) [12]:

9f,L (; 1, Y)=etL (; 1,0)exp(- 9 y )+b 2 j 0 (; 1 )Zk; d,F2 k (; 1)+ k=0

+ b0 ZAnSx,n, 1 ZAmF3(ym,91, Y)9ck,l(цт, Ym ), n=0         m=0

где

Y

^F 2,p ^{( 9} 1 , ^Y M z p exP^{[ 9} 1 ^{( Z - Y )] dz} =

I y ^p

^exP^{( -9} 1^{Y )]}/ ⁹ 1 - pF 2,p—1 ( 9 1 , Y )

при p = 0, при p > 0;

/

F 3 ( y m , 9 1 , Y ) - ^YK у ( y m Z ) exp ( -9 _zz ) dz =

= exp ( -9 1 Y ) [ y 2m F 4 ( y m Y ) -9 K у ( y m Y ) ] + 9₁ + Bi 0 9 2 +y m                    ’

^F 4 ⁽Y m^Y ) -^[ s'n ⁽Y m^{Y )- Bi}0 cos ⁽Y m^Y ^Y m У Y m .

Оригиналы температур каркаса и теплоносителя находятся по формулам обращения [10]:

да                    да

9 ск ( X , Y ) = Z A n J 0 ( ц . X ) Z A m K y ( y m Y ) 9 cKL ( ц n , Y m ) , n = 0             m = 0

да

9 f ( X , Y ) = Z A 1 J 0 ( ; 1 X )e_tt ( ; 1 , Y ) , (14) l = 0

где A n = ^J 1 ^(ц n )/^{( ц} n^S x, n ) ^{; S} x, n = ^J 1 ^(ц n )/ ^{2 ;} A m = ^F 1,0 ^(y m ⁹⁾/ ^S 2, m ; ^S У, ^m =^{i K} У ^(y m^Y ) d ^Y ;

2   22   2

A 1 = ^J 1 ^(; 1 // ( S 1^S x, 1 ) ; ^S x, 1 = ^J 0 ^(; 1 ^{) + J} 1 ^(; 1 ^{)] 2} .

Интегрирование решений (13) и (14) по радиусу дает средние по поперечному сечению температуры

9ск (Y) = 2i X .ecK (X, Y)dX ;

9f (Y) = 2i X -ef (X, Y)dX, а последующее интегрирование по длине – температуры, средние по объему пористого тела

9 ск = 2 ii X -e _cK ( X , Y ) dXdY ,

9 f = 2 ii X -9 _f ( X , Y ) dXdY .

По средним температурам находятся теплота, передаваемая теплоносителю конвекцией от стенки и пористого тела

Q a = П R1 ц a w t * ( 28 s + Rf w ) ( 9 ск -9 f ) . (15) и теплота, равная разности энтальпий теплоносителя между выходом и входом

Q c = G f c p,f t ‘ [ 9 f (1)-е„> ] .         (16)

В формулу (15) коэффициент теплоотдачи a w входит как параметр - от его значения зависят как температурные поля, так и тепловые нагрузки Qa и Qc. Но теплота Qc может отличаться от Qa, если доля теплоты ^q , отданная стенкой каркасу, будет оценена неточно. Отсю- да следует простой способ оценки значения ηQ при известном значении коэффициента теплоотдачи αw : задав начальное приближение η(Q0) , находятся температурные поля и тепловые нагрузки Qα и Qc . При значительном расхождении последних величина ηQ уточняется, находятся новые значения Qα и Qc до их совпадения с заданной точностью.

ПРИМЕР ТЕПЛОВОГО РАСЧЕТА ПОРИСТОГО ЦИЛИНДРА

Пористый цилиндр из нержавеющей стали 1Х18Н10Т со структурой ВПЯМ диаметром D = 0,05 м, длиной l _ц продувается воздухом. Пористость характеризуется параметрами: d _сф = 2·10^-3 м; ε _v = 0,88; l = 3,5·10^-3 м; ε _s ≈ 0,511; d _э = 1,895·10^-3 м; f _w ≈ 1858 м^-1; d _ск ≈ 0,258·10^-3 м; ε _ск ≈ 0,0438. Параметры воздуха на входе: t _f,0 = 20 °С; p _f,0 = 0,101 МПа; относительная влажность 80%. Температура стенки по длине неизменна и составляет t _ст = 90 °С. Теплоотдача в пористом теле определяется критериальным уравнением [12]

Nu = 0,606Re^0,56 Pr^0,4 ε _v ^{- 5,2} , (17) где Re = w _f d _сф / ^λ f .

Расчеты выполнены для длин цилиндра l _ц от 0,01 до 0,1 м, при двух расходах G _f : 0,004 и 0,04 кг/с – и двух вариантах значений коэффициентов теплоотдачи на торцах цилиндра: 1) α ₀ = α ₁ =α _w и 2) α ₀ = α ₁ = 0 . Коэффициент теплоотдачи α _w для разных значений l _ц изменялся в диапазонах 365,4…368,5 Вт/(м²К) при G _f = 0,004 кг/с и 1322…1337 Вт/(м²К) при G _f = 0,04 кг/с (меньшие значения α _w соответствовали короткому цилиндру, большие – длинному).

Учет теплоотдачи на торцах наиболее заметен для короткого пористого тела. Причем с увеличением длины разность между тепловыми нагрузками, рассчитанными с учетом и без учета теплоотдачи торцов сокращается по абсолютному значению и меняет знак: при малых значениях lц большее количество теплоты получается в первом варианте ( α0 = α1 = αw ), при больших lц – во втором ( α0 = α1 = 0). Эта закономерность наиболее ярко проявляется на больших расходах. Так, если при Gf = 0,004 кг/с для длин пористого тела 0,02 и 0,1 м разница между тепловыми нагрузками для указанных вариантов составила соответственно 0,3 Вт (0,12%) и -0,16 Вт (-0,06%), то при Gf = 0,04 кг/с эта разница составила уже 21,5 Вт (около 1,5%) и -7,9 Вт (-0,3%).

Таким образом, учет теплоотдачи торцов пористого цилиндра должен осуществляться, прежде всего, при малой его длине; при большой длине вкладом теплоотдачи торцов можно пренебречь из-за пренебрежимо малой площади поверхности каркаса на торцах цилиндра по сравнению с его общей площадью теплообмена.

Доля теплоты η Q , воспринимаемая от стенки каркасом, максимальна в случае короткого пористого тела и растет с повышением расхода теплоносителя. Так, при l _ц = 0,02 м η Q составляет 0,9946 при расходе 0,004 кг/с и 0,9999 – при 0,04 кг/с; при l _ц = 0,1 м значения η Q соответственно равны 0,9789 и 0,9973. Близость значений η Q к единице говорит о том, что наибольший вклад в процесс передачи теплоты от стенки к теплоносителю вносят теплопроводность и последующий конвективный теплообмен каркаса с теплоносителем. Причиной тому являются, с одной стороны, на порядок более высокие, чем λ _f,эф значения λ _ск (примерно, в 26 раз), а с другой – сравнительно небольшая доля поверхности цилиндрической стенки (примерно, 4,1%) от общей поверхности теплоотдачи. Поэтому каркас играет роль радиатора, отводящего теплоту от стенки.

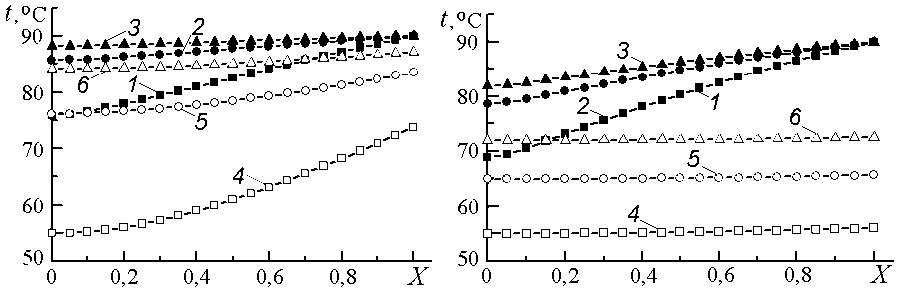
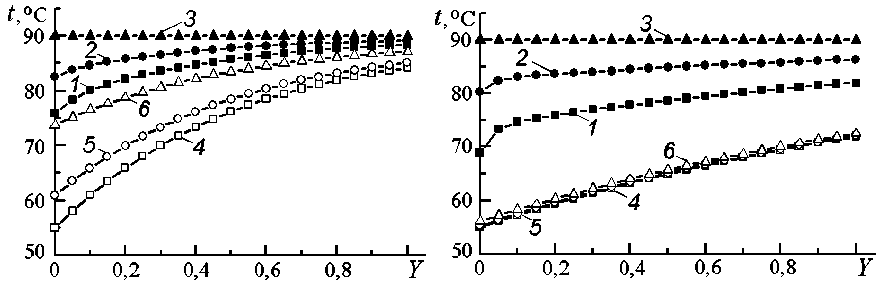
Результаты расчетов, показанные на рис. 2 и 3 для l _ц = 0,02 м, свидетельствуют о том, что с увеличением расхода G _f диапазон температур

а )

б )

Рис. 2. Радиальное распределение температур каркаса ( 1 -3) и теплоносителя ( 4-6 ) на входе ( 1, 4 ), в средней части ( 2, 5 ) и на выходе ( 3, 6 ) из пористого тела а – G _f = 0,004 кг/с; б – G _f = 0,04 кг/с

а )

б )

Рис. 3. Продольное распределение температур каркаса ( 1 -3) и теплоносителя ( 4-6 ) на оси ( 1, 4 ), на среднем радиусе ( 2, 5 ) и на стенке ( 3, 6 ) пористого тела а – G _f = 0,004 кг/с; б – G _f = 0,04 кг/с

в каркасе растет, а поле температур в потоке теплоносителя, особенно в радиальном направлении, наоборот – становится более однородным. По характеру продольного распределения температур, показанного на рис. 3, видно, что при t ст = const теплота, отдаваемая теплоносителю, неравномерно распределяется по длине пористого цилиндра – входная часть является более теплонапряженной, чем выходная. Причем с увеличением расхода эта неравномерность усиливается. На подобное обстоятельство указывается и в литературе [7].

Следствием неравномерности распределения теплонапряженности по длине пористого тела является зависимость тепловой нагрузки от длины пористого тела, показанная на рис. 4. Здесь Q = QQ 0 ; Q о - базовая тепловая нагрузка, за которую принята нагрузка при l _ц = 0,02 м, равная 268,6 Вт при G _f = 0,004 кг/с и 2168 Вт – при G _f = 0,04 кг/с.

Рис. 4 наглядно показывает, что при G f = const , начиная с некоторого значения l _ц,max , наступает режим автомодельности – теп-

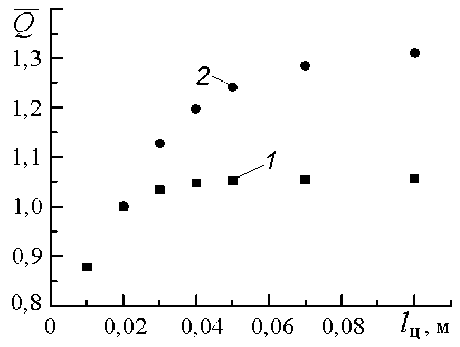
Рис. 4. Влияние длины пористого цилиндра на относительную тепловую нагрузку 1 –Gf = 0,004 кг/с; 2 –Gf = 0,04 кг/с ловая нагрузка достигает наибольшего значения Qmax и перестает зависеть от lц . В свою очередь, величины lц,max и Qmax зависят от расхода: с увеличением Gf значения lц,max и Qmax также возрастают.

МЕТОДИКА ИССЛЕДОВАНИЯ ТЕПЛООТДАЧИ В ПОРИСТОМ ЦИЛИНДРЕ

Целью исследования является определение коэффициента теплоотдачи a w и числа Нуссельта Nu в пористом цилиндре при заданной геометрии цилиндра и характеристиках пористости, и полученных путем прямых измерений значений расхода G _f , температуры стенки t _ст и парамет р ов теплоносителя на входе t _f,0 и p _f,0 и выходе t _f,к и p _f,к из рабочего участ к а в серии опытов. По значениям G _f , ^t f,0 , p f,0 , t f,к и p f,к теплоносителя рассчитывается опытная тепловая нагрузка (16) в каждом опыте.

Методика определения a w в отдельном опыте основана на последовательном задании ряда значений этой величины с последующим расчетом температур по уравнениям (13), (14) и расчетной тепловой нагрузки (15) для каждого значения a w . Искомое значение a w соответствует равенству расчетной и опытной нагрузок в рассматриваемом опыте.

Найденные таким образом величины a w и Nu для серии опытов с разными значениями G _f , t _f,0 , p _f,0 , t _f,к , p _f,к и t _ст дают возможность построить критериальное уравнение теплоотдачи вида Nu = f ( Re, Pr, А т , n _т ,... ) , где A _т , n _т -искомые постоянные.

ПРОВЕРКА МЕТОДИКИ ИССЛЕДОВАНИЯ ТЕПЛООТДАЧИ НА МОДЕЛЬНОЙ ЗАДАЧЕ

Достоверность методики определения величины aw можно оценить лишь тогда, когда заранее известно ее истинное значение. За истин- ные имеет смысл принять те значения αw , по которым предварительно был произведен прямой тепловой расчет пористого тела. Полученные в результате этого расчета для ряда расходов Gf значения tf,0 , pf,0 , tf,к , pf,к и tст являются исходными данными для определения ряда соответствующих значений αw .

Для проверки устойчивости метода исследования αw к погрешностям исходных данных к значениям Gf , tf,0 , tf,к , pf,0 , pf,к и tст , полученным из прямого теплового расчета рассмат- риваемого пористого тела, с помощью генератора псевдослучайных чисел добавляются погрешности Δt = δt ⋅ tпр , ΔG = δG ⋅ Gпр и Δp = δp ⋅ pпр . Здесь δt, δG и δp – относительные погрешности; tпр , Gпр и pпр – пределы измерений величин.

Проверка методики исследования теплоотда- чи произведена на примере охлаждаемого воздухом пористого цилиндра, описанного выше.

Прямые тепловые расчеты пористого цилиндра выполнены при исходной температуре стенки tст = 90 оС, в диапазоне расходов воздуха от 0,004 до 0,04 кг/с и давления перед пористым телом от 1,1 до 1,3 бар. Проведены две серии ма- тематического эксперимента, отличающиеся друг от друга относительными погрешностями. В первой серии относительные погрешности составляли: δt = δp = δG = 0; во второй серии: δt = δp = 1 %, δG = 3 %. Предельные значения величин: tпр =100 оС; Gпр = 0,05 кг/с; pпр = 1,5.105 Па.

Полученные значения коэффициентов теплоотдачи показаны точками на рис. 5. Здесь светлым точкам соответствуют найденные по описанной методике значения Nu ≡ Nu/ ( Pr ^0,4 ε _v ^{- 5,2} ) . Квадратным точкам и аппроксимирующей их линии 1 отвечает случай

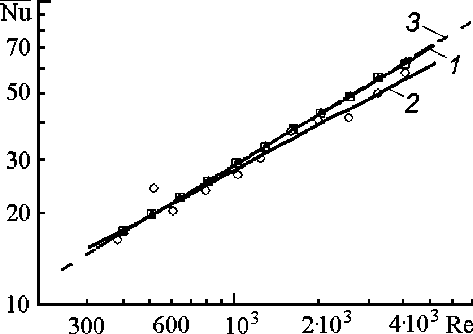
Рис. 5. Результаты исследования теплоотдачи в первой ( а ) и второй ( б ) сериях: 1 – уравнения (18); 2 – уравнение (19);

3 – уравнение (17)

δ t = δ p = δ G = 0; круглым точкам и линии 2 – случай δ t = δ p = 1 %, δ G = 3 %. Темные треугольные точки и пунктирная линия 3 соответствуют исходному, или “истинному” критериальному уравнению, в качестве которого взято уравнение (17). Аппроксимация точек с помощью метода наименьших квадратов позволила получить следующие уравнения регрессии:

Nu = 0,628Re ^0,5545 , σ = 0,7% : r = 99,987%. (18)

Nu = 0,909Re^0,496, σ = 8%: r = 98,1%. (19)

Практически полное совпадение линий 1 и 3 на рис. 5 говорит о том, что в идеальном случае, то есть при отсутствии погрешностей прямых измерений в первой серии расчетов, изложенная методика позволяет найти истинные значения коэффициентов теплоотдачи. Погрешности, внесенные в исходные данные во второй серии расчетов, приводят к отклонениям найденных α _w от истинных значений. Однако, даже при довольно больших принятых погрешностях исходных данных максимальное отклонение линий 2 и 3 (при Re = 4100) не превысило 12%, что считается допустимым в теории теплообмена.

ЗАКЛЮЧЕНИЕ

• 1.    Предложена аналитическая модель теплофизических процессов в пористом цилиндре, нагреваемом внешним источником энергии, которая позволяет оценить долю теплоты, отводимую от стенки каркасом.

• 2.    Расчеты теплового состояния пористого цилиндра показали физически обоснованные результаты по температурным полям и тепловой нагрузке, передаваемой от стенки через каркас теплоносителю.

• 3.    Показано существование предельной длины пористого тела, выше которой тепловая нагрузка остается неизменной для фиксированного расхода теплоносителя.

• 4.    Предложена методика исследования теплоотдачи в пористом теле на основе модели тепловых процессов, протекающих в нем при теплообмене с однофазным теплоносителем.

• 5.    Проверка показала удовлетворительную устойчивость модели к погрешностям исходных данных и сходимость получаемых с помощью предложенной методики результатов исследования теплоотдачи к их истинным значениям.

Работа выполнена в рамках реализации ФЦП “Научные и научно-педагогические кадры инновационной России” на 2009-2013 годы, Государственный контракт № П2516 от 20 ноября 2009 г.