Математическая модель уплотнения почвы комлями пачки хлыстов при их трелевке

При анализе процессов трелевки древесины одной из основных задач является установление особенностей деформации и уплотнения почвогрунта при воздействии на него отдельных элементов трелевочной системы (ТС) - движителя, кроны деревьев, комлей и вершин хлыстов.

Одномерные модели уплотнения почвы в границах волока в результате циклического воздействия движителя ТС нашли свое применение в работах [1], [2], [3]. Объемная модель деформирования грунта [8] использована в задаче минимизации вредного воздействия движителя на почвогрунт как в границах волока, так и за его пределами в боковых полосах с целью охраны подроста и его корневой системы при многократном проходе ТС по заранее намеченным трассам волоков.

Однако в процессе трелевки точно выдержать заданное направление движения не представляется возможным, и ТС вынуждена совершать поворотные движения. Это обусловливает возникновение дополнительных касательных напряжений в направлении, перпендикулярном действию нормальной нагрузки движителя, которые оказывают разрушающее действие на по- чвогрунт и отрицательно влияют на ее плодородие и качественную структуру [3], [7].

Наряду с отмеченными оценками поворотного воздействия движителя представляют особый интерес исследования воздействия на почвогрунт веса пачки, в частности ее комлевой части, поскольку в этом случае возникает дополнительное уплотнение почвогрунта.

В рамках расчетной схемы воздействия комля хлыста на почвогрунт [3] с учетом оценки доли действующего объема и веса пачки деревьев [4] рассмотрим схему (рис. 1) давления на почвогрунт сосредоточенной силы Q = P + G , где Q - сила тяжести хлыста, P = 0,3 Q - сила тяжести хлыста, действующая на трактор, G = 0,7 Q - сила тяжести хлыста, действующая на почву при трелевке его за вершину, в результате чего часть хлыста может погружаться в почвогрунт на определенную величину первичной зоны осадки h о .

На рис. 1 а представлена схема погружения комлевой части хлыста 1, где обозначено: М -центр тяжести хлыста, h_K - расстояние от точки 2 опоры хлыста на конике до опорной поверхности 3, L - длина хлыста, l - длина хлыста в зоне касания и погружения на глубину h о .

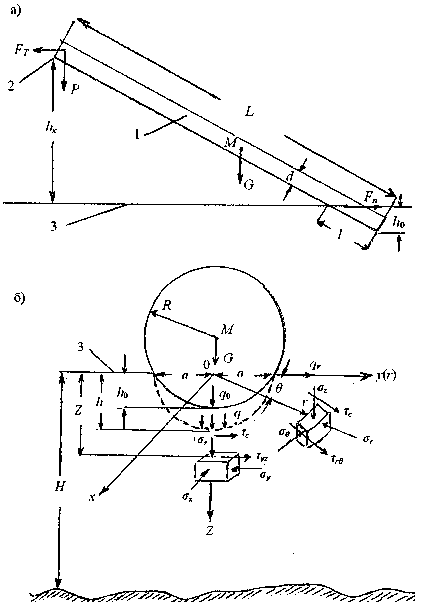
Рис. 1. Схема расчета напряжений при воздействии комля хлыста на почвогрунт: а - схема погружения комлевой части хлыста; б - схема расчета напряжений

Величина h о на основании [6] с учетом связи условного радиуса комля, получаемого по таксационному значению диаметра ствола d , определяется в виде:

Такое представление действующей части хлыста на почвогрунт позволяет использовать математическую модель деформирования среды на основе принципов механики контактного разрушения при воздействии сферического индентора радиусом R на упругое полупространство [5].

В рамках этой модели основными характеристиками процесса погружения индентора в среду являются величины контактного сбл иже ния h о и радиуса контактной площадки a = ^h ₀ R , на которой действует усредненное по площади на-

GG чальное равномерное давление q o = —2 = —г. a   л п ₀ R

Оценим начальные параметры контакта при следующих исходных данных нагружения почвогрунта.

Трелевка одиночного хлыста осуществляется при следующих исходных данных: L = з0,5 м; d = 0,24 м; V = 0,65 м³; G = 2,275 кН; h = 1,8 м; l = 1,525 м, в x = 1,05.                       ^к

Почвогрунт волока является связным влажным грунтом с величиной влажности W, приблизительно равной величине предела текучести W_T [1]. Начальная плотность естественного сложения почвогрунта принимается р о = 800-900 кг/ м³; модуль Юнга Е = 1 МПа; величина внутреннего сцепления С =12 кПа; угол внутреннего трения ф = 15^о; несущая способность q s = 30 кПа; коэффициент Пуассона v = 0,25; Н = 0,4 м.

В соответствии с методическими положениями [2], [6] для таких условий нагружения установлены значения коэффициентов А = 0,0564 м. е. и n = 1,0206, входящих в формулу (1), получены следующие параметры контакта:

h

з -Я hG n ⁺1,5 .3 ^Р ALjd

,

где коэффициент в > 1 представляет собой отношение величины L к максимально возможной подвешенной части длины хлыста; A и n - параметры почвогрунта и штампа весом G с пятном контакта d в степенных зависимостях q = Ah n , то есть зависимостях величины давления (нагрузки) штампа q от глубины его погружения h [1], [2], [6] в пределах от 0 до глубины Н зоны распространения деформаций (удаленности от твердого слоя).

На рис. 1б представлена схема расчета напряжений, возникающих в почвогрунте под действием силы G в пределах зоны деформаций Н , в процессе контакта и погружения комлевой части хлыста с учетом его возможного поворота на определенный угол 9.

Действующая на грунт часть хлыста объемом в коре V x определяется в соответствии со значениями L и d по сортиментным таблицам древостоев и в расчетах представлена как эквивалентная по объему и весу сфера радиусом r = з р⁷^ с центром в точке М . ' ⁷¹

h _о = 0,047 м; a = 0,157 м; R = 0,53 м; q о = 41,64 кПа. (2)

Процесс деформирования почвогрунта за пределами зоны контакта глубиной h _о и радиусом а рассмотрим в декартовой системе координат, причем на элементарных площадках массива действуют напряжения (рис. 1б), определяемые в соответствии с соотношениями [5]: а) вертикальное напряжение:

/     33      2

z au

O z =- q 0У ^{,( (} r , ^z ) = - q 0        2—тт,      (3а)

IV u u +az

б) горизонтальное напряжение:

p = q o v/ r z),

(3б)

где

, x 1"2v a2

(У y ( ^Г , ⁽ ) = —--——

3 r + z

1-(    ) ³

u

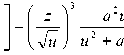
z

u

(1 - r) u a ² + u

+ (1 + v) arctg      - 2 ,

u

в) тангенциальное напряжение:

^T yz = -q 0 V '^ ⁽ r . ^z ) = - q 0

a ² V uz ²( r ² + z ²)

( u +a ²)( u ² + a² z ² )

(3в)

где ψ_z ( r , z ), ψ_y ( r , z ) и ψ_yz ( r , z ) – так называемые координатные функции, u – положительный корень r ²       z ²

квадратного уравнения 2 Н— = 1.

a ² + uu

Компонента σ_x может быть определена через механизм бокового расширения грунта в виде

V

σ x = -----(Т ^.

x z

1 ^z

Поскольку задача рассматривается в осесимметричной постановке, ось y может быть заменена на ось r , где r – радиальное расстояние от центра контакта до расчетной точки, то есть принимаем σ_у = σ_r .

Как следуе ^у т из анализа соотношений (3), напряженное состояние почвогрунта зависит от координат расчетной точки и радиуса контактной площадки а , которая, в свою очередь, зависит от h _о и R .

На рис. 2 для исходных данных контакта (2) представлены зависимости изменения безразмерных функций ψ_z ( r , z ), ψ_y ( r , z ) и ψ_yz ( r , z ) от относительной величины h = z / h _о непосредственно под сферическим индентором ( r = 0). Анализ данных рис. 2 позволяет сделать ряд выводов. Во-первых, отрицательные (сжимающие) вертикальные σ_z и преимущественно положительные (растягивающие) радиальные напряжения σ_r свидетельствуют о том, что разрушение массива грунта происходит через механизм сдвига. Во-вторых, тангенциальные напряжения τ_yz по величине близки к нулю и слабо изменяют ^y ся с глубиной по мере роста координаты z . Это означает, что компоненты σ_z , σ_у и σ_х можно принять за главные – соответственн ^у о σ ₁, σ ₂ и σ ₃.

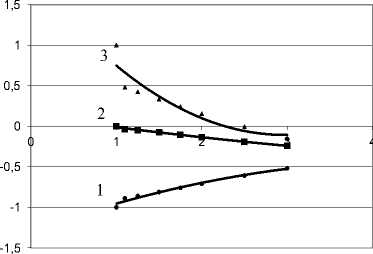
Рис. 2. Характер изменения координатных функций под сферическим индентором:

1 – ψ_z ( r , z ), ( у = -0,0411 х ²+ 0,3792 х - 1,2919, R ²= 0,9761);

2 – ψ^z ( r , z ), ( у = 0,2212 х ²- 1,3121 х + 1,8398, R ²= 0,8601);

3 – ψ_y^y_z ( r , z ), ( у = 0,0088 х ²- 0,1504 х + 0,1305, R ²= 0,9942)

Поскольку на почвогрунт кроме вертикальной силы G действует касательная (горизонтальная) сила FТ тяги трактора, необходимая для трелевки хлыста, то возникает сила Fп сопротивления его скольжению, в результате происходит деформация почвогрунтагрунта в направлении действия этой силы (рис. 1а). Следствием этого является формирование горизонтальных напряжений τс, перпендикулярных действию вертикальных напряжений σz и обусловливающих реализацию разрушения массива почвогрунта через механизм сдвига (рис. 1б).

Горизонтальные напряжения τ _с связаны с вертикальными σ _z обобщенным законом Кулона:

Тc = СУ_ztgф* C .                  (4)

В момент отклонения ТС и, следовательно, хлыста от заданного направления движения на угол θ деформирование почвогрунта целесообразно рассмотреть в цилиндрической системе координат zrθ .

Компоненты тензора напряжений в этой системе в общем случае при наличии касательных напряжений τ_rθ , совпадающих по направлению с действием горизонтальных напряжений τ_с , определяются соотношениями:

z 1 ;

_r 2     3      2     3 cos2 е ;

^r 2          2

2     3      2     3 cos2 е ;

_r ^{2     3} sin2 е .

r а         ₂

Из соотношений (5) следует, в частности, что при θ = 0 компоненты тензора напряжений являются главными, то есть имеем:

σ_z = σ ₁, σ_r = σ ₂, σ_θ = σ ₃, τ_rθ = 0.

Результирующая величина τ = τ_с + τ_rθ будет характеризовать суммарные сдвиговые напряжения и в качестве критерия разрушения можно принять условие превышения величиной τ предела несущей способности почвогрунта q_s , то есть:

τ ≥ q^s . (6)

Величину z , при которой выполняется условие (6), можно рассматривать в качестве предельной величины контактного сближения или максимально возможной глубины зоны осадки хлыста h_s .

Определив с помощью (3) компоненты тензора напряжений, на основании соотношений (4) и (5) вычислили суммарные сдвиговые напряжения τ , кПа в зависимости от относительной координаты h для различных значений угла поворота θ в пределах от 0 до 25^о.

В результате установлено, что при трелевке одиночного хлыста по данному почвогрунту без каких-либо маневров ТС критерий разрушения с д вигом (6) за пределами контактной площадки ( h = 1) не выполняется, то есть за пределами первичной зоны осадки ( z = h _о = 0,047 м) разрушение почвогрунта сдвигом не происходит.

В случае если наблюдаются повороты хлыста (угол θ изменяется от 10 до 25^о), создаются условия для формирования дополнительной зоны осадки, глубина которой h_s увеличивается с 0,058 до 0,082 м ( h изменяется от 1,25 до 1,75). Величина радиуса контактной площадки а возрастает в этом случае с 0,176 до 0,208 м.

Указанным значениям hs в силу принятого закона изменения q(h) и полученных коэффициентов A и n соответствуют величины нагрузки q на почвогрунт от сферического индентора радиусом R в диапазоне от q = 27,3 до q = 48,33 кПа.

Обработка данных методами корреляционнорегрессионного анализа позволила с достаточно высоким коэффициентом детерминации (R2 > 0,93) определить для трелевки одиночного хлыста зависимость т от h с учетом углового параметра 9: _ т = X hn, (7) где коэффициенты X и n являются функциями угла 9:

X = 0,7605 9 + 23,913; n = -(0,0179 9 + 0,241).   (8)

Из соотношений (6) и (7) следует, что предельную глубину зоны осадки hs можно опреде- лить в виде:

hs

= h 0

qs

Тогда величина относительного уплотнения почвогрунта в границах волока определяется как [2]:

р = р/ _{= £ +} 1 = h i + 1, (10) /Р 0 H ⁷

где р - достигнутая плотность грунта, £ - деформация уплотнения.

Радиальное давление q_r вдоль радиуса r >  a , отсчитываемого от границы контактной площадки, описывается уравнением эллипса [5]:

q,=q qVw a / ^{r ) 2} .              (11)

Как видим, на границе площадки при r = a величина q r = 0 и с ростом относительного расстояния r / a будет возрастать.

Предельное радиальное расстояние r_s , при котором величина q_r превысит величину несущей способности грунта q_s , можно трактовать как размер максимальной зоны уплотнения в радиальном направлении от колеи или как размер (ширину) охранной полосы корневой системы подроста или оставляемых на корню деревьев.

Таким образом получим:

,s=a L ¹ 2V                (12)

q_S ¹         2

q 0

Используя соотношение (12) при исходных данных q s = 30кПа и q о = 41,64 кПа, установили, что для одиночного хлыста диапазон изменения r_s составляет 0,25-0,30 м.

Выполнив аналогичные расчеты для более широкого диапазона изменения угла поворота хлыста ( 9 = 0-45^о), фиксировались предельные значения h_s , a , r_s , после чего оценивалась величина деформации уплотнения £ . На рис. 3 представлены зависимости деформации уплотнения £ и размера охранной полосы r s от угла 9° при трелевке одного хлыста ( N_x = 1) и одном двойном проходе ТС по одному и тому же волоку ( N = 1).

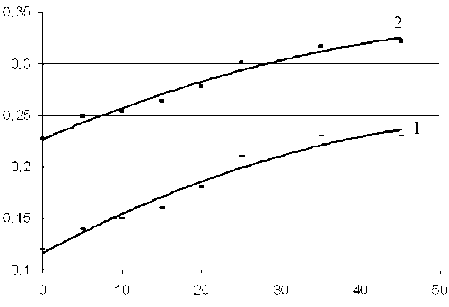
Рис. 3. Зависимость деформации уплотнения (1) и размера охранной полосы (2) от угла поворота 9

Видно, что маневры ТС существенно влияют на величину £ (диапазон изменения е составляет от 0,12 до 0,23) и, соответственно, на величину относительного уплотнения р, тогда как размер охранной полосы остается в более узком диапазоне r s = 0,23-0,33 м.

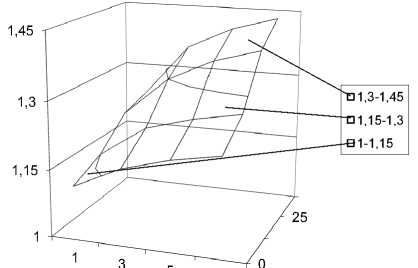
Данные рис. 4 отражают характер совместного влияния цикличности и маневренности ТС на величину относительного уплотнения г. Число ( N ) проходов ТС по одному и тому же волоку учитывалось путем умножения расчетной величины £ на коэффициент X N = 1 + lg N [2]. Анализ данных рис. 4 свидетельствует о значительном диапазоне изменения величины г даже при трелевке одиночного хлыста.

1,45

1,3

1,3-1,45

1,15-1,3 1-1,15

1,15

Рис. 4. Влияние угла поворота хлыста на процесс циклического уплотнения почвы

Разработанная математическая модель воздействия одиночного хлыста на почву явилась основой для расчета трелевки пачки аналогичных хлыстов в количестве N_x = 2, 3-10 штук объемом до V = 6,5 м³ и весом до Q = 32,5 кН (G = 22,75 кН) "

Получены следующие начальные параметры контакта при значении N_x = 10:

h о = 0,117 м; a = 0,363 м; R = 1,13 м; q о = 78,3 кПа, (13) для которых сделаны расчеты по выполнению критерия разрушения (6) на основе оценки компонент тензора напряжений (3). В конечном счете были установлены параметры уплотнения почвогрунта р и размеры охранной полосы r s .

На рис. 5 представлены результаты расчетов в системе обозначений рис. 3. Абсолютные значения величины r_s существенно выросли, и диапазон их изменения составил r_s = 1,1–1,6 м. Деформация уплотнения почвогрунта ε при этом также увеличилась и достигла значения 0,8.

Влияние угла θ и параметра цикличности N на величину уплотнения почвогрунта отражено на рис. 6, где отложены значения р и 6 ° для четырех значений величины N = 1, 3, 5, 7.

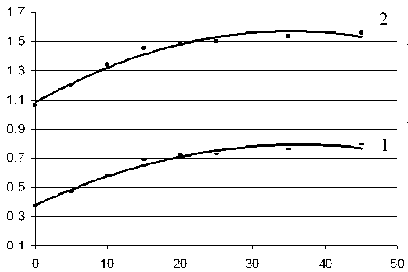
Рис. 5. Зависимость деформации уплотнения и размера охранной полосы от угла поворота пачки хлыстов

Сопоставим полученные расчетные данные с опытными значениями результатов исследования законов распределения изменения плотностей ρ почвогрунтов под движителем от естественного сложения до десятого двойного прохода ТС по волоку при трелевке пачки хлыстов длиной L = 24 м и d = 0,26 м [3].

Для участка прямолинейного движения ( θ = 0^о) при одном двойном проходе ТС экспериментальная плотность почвогрунта ρ возрастает с 8 70 до 1135 кг/м³, то есть величина уплотнения ρ = 1,305. График 1 рис. 6 для оценки уплотнения почвы под хлыстами дает расчетное значение ρ = 1,365.

При N = 7 опытные значения плотности достигли величины ρ = 1750 кг/м³, то есть относительное уплотнение составило ρ = 2, тогда как расчетное значение ρ = 1,68. Это позволяет заключить, что процессы уплотнения почвогрунта от нагрузки движителем и пачкой хлыстов сопоставимы и характеризуются близкими по величине параметрами относительного уплотнения ρ .

Ограничивая сверху величину ρ значением 2, что означает уплотнение влажного почвогрунта на всю глубину H зоны распространения деформаций, то есть вплоть до основания твердого слоя, можно сделать вывод о том, что рост величины N диктует необходимость существенного снижения маневров ТС или соответствующего снижения веса пачки.

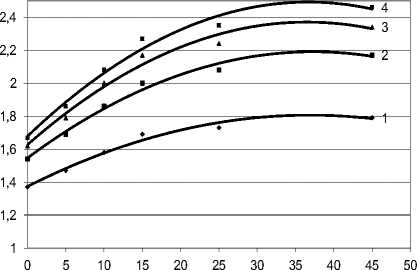
Рис. 6. Изменение ρ ( θ ) в зависимости от числа N проходов ТС:

1 – один проход ТС ( у = -0,0006 х ² + 0,0444 х + 1,6778; R ² = 0,9815); 2 – три прохода ТС ( у = -0,0006 х ² + 0,0408 х + 1,6267; R ²= 0,9797); 3 – пять проходов ТС ( у = -0,0005 х ² + 0,0345 х + 1,5457; R ²= 0,9868); 4 – семь проходов ТС ( у = -0,0003 х ² + 0,0235 х + 1,3729; R ²= 0,981)

Выполнению первого условия способствует то обстоятельство, что увеличение предельной глубины зоны осадки h_s , то есть глубины образованной в процессе погружения ТС колеи, препятствует существенному отклонению ТС от заданного направления. Выполнение второго условия ограничено технологическими схемами трелевки и требует выполнения специальных исследований по оптимизации параметров ТС с учетом несущей способности почвогрунта в пределах проектных схем расположения волоков.

Обобщая установленные закономерности уплотнения почвогрунта под действием веса пачки хлыстов, можно отметить необходимость выполнения исследований по оценке предельных значений веса пачки и параметров ее трелевки по конкретным волокам, обеспечивающих в границах волока с учетом допустимых размеров охранных полос оптимальное уплотнение почвогрунта в заданных пределах.