Математическая модель уплотняющего воздействия динамики поворота лесозаготовительной машины на боковые полосы трелевочного волока

Лесозаготовительная техника воздействует на все компоненты лесной среды: деревья, остающиеся на доращивание, подрост, и особенно на почвогрунты, вызывая уплотнение почвогрунтов на технологических коридорах и вокруг них, колееобразование и минерализацию верхнего почвенного слоя. В результате уплотнения почвы уменьшается эффективный размер пор, что затрудняет циркуляцию почвенного воздуха, снижая содержание в нем кислорода. Согласно [4] для активного роста кончиков корней концентрация кислорода должна достигать 5-10 %; при концентрации кислорода менее 1 % корни заметно теряют в весе. Независимо от глубины стержневых крупных корней основная масса всасывающих корешков и корневых окончаний расположена в верхнем слое почвы, поскольку он обладает лучшими физико-химическими свойствами, содержит основное питание и обеспечивает достаточный подвод кислорода к корешкам за счет наличия почвенных пор. Если почва не уплотнена, то корневые ходы, трещины и другие внутрипочвенные полостные образования способствуют усиленному развитию корней и обеспечивают их прирост. В противном случае происходит их угнетение. Уплотнение почвы ведет также к резкому снижению скорости фильтрации воды, затрудняя проникновение влаги в глубинные слои, способствуя застою воды в углублениях, что также отрицательно влияет на жизнь растений. Избыток влаги нарушает деятельность почвенных микроорганизмов, играющих важную роль в обеспечении корней растений доступными элементами питания. Негативно сказываются на лесном массиве и колееобразовательные процессы. Глубокая колея ведет к разрушению большей части корневой системы, попадающей на волок, может служить накопителем излишней влаги, а также способствует водной эрозии.

Вопросы выбора машин и технологий лесозаготовок с целью снижения отрицательного воздействия на почвогрунты рассматривались в работах [5], [6], [7]. В [6] главное внимание было уделено колееобразованию, а в [5], [7] - уплотнению почвогрунтов, причем в [7] исследовалось уплотнение почвогрунтов не только в области волока, но и за его пределами. В [7] рассматри-

вались напряженные состояния среды, вызванные поворотами гусеничных движителей при движении по волоку. В случае колесной техники неизбежно возникающие при движении транспортного средства многочисленные удары колес движителя о дно и боковые стенки колеи вызывают в среде волны деформаций. Это также ведет к уплотнению грунта за пределами волока.

Грунт представляет собой сложную многофазную дисперсную систему, макроскопическое поведение которой под действием нагрузок определяется протеканием многих параллельно идущих процессов различной механической природы. Для феноменологического описания напряженно-деформированного состояния и процессов в грунтах привлекают представления и методы механики сплошных сред, используя различные реологические модели для учета качественных и количественных характеристик деформационных процессов. Многообразие природных разновидностей грунтов и условий воздействия на них ведет к соответствующему многообразию форм макроскопического поведения среды. Для описания грунтов [3] широко применяют модели: Гука, Кельвина - Фойгта, Максвелла, Сен-Венана, Шведова, в которых для описания поведения материала под действием механических нагрузок используются три типа элементов - упругая пружина, вязкий демпфер и пластический шарнир. Все эти модели, однако, обладают симметрией по отношению к растяжению и сжатию, тогда как характерной особенностью грунтов является различное сопротивление растяжению и сжатию с нелинейной зависимостью между деформациями и напряжениями при нагрузках и разгрузках. Как показывают многочисленные эксперименты [9], при любых по интенсивности воздействиях на среду при разгрузке возникают остаточные деформации. Слабые воздействия и малые деформации среды, возникающие в грунте вне трассы при движении лесозаготовительной техники, накапливаясь, могут приводить к заметному уплотнению грунта.

Существуют разные подходы к тому, как учесть различное сопротивление при растяжениях и сжатиях. Так, в [8], чтобы учесть различное сопротивление материала, реологический метод дополняется новым элементом - жестким контактом, моделирующим идеально сыпучую среду с жесткими частицами. Используя жесткий контакт в сочетании с традиционными элементами, можно строить реологические схемы материалов со сложным комплексом механических свойств. Другой подход предлагается в теории гипопластичности [10], в которой связь напряжение - деформации представляется нелинейным эволюционным уравнением с коэффициентами, в общем случае зависящими от параметров напряженного состояния и пористости среды, а также от констант, характеризующих типы материалов и определяемых из экспериментов и расчетов. Результаты изучения некоторых закономерностей распространения волн в грунтах на основе гипопластической модели среды представлены в [1]. Наше рассмотрение опирается на это исследование. Представлено общее теоретическое обсуждение волн в грунтах, а также приведены оценки уплотнения почвогрунта. Показано, что выбором скоростного режима лесозаготовительного транспорта можно заметно воздействовать на этот механизм уплотнения почвогрунтов.

В механике сплошных сред изменение импульса среды определяется уравнением

Pdv. = ^,_, i, j = i, 2 з, (1) dt dxj здесь p - плотность среды, v . - скорость частиц среды, ay - тензор напряжений, х. - декартовы координаты, по повторяющимся индексам проводится суммирование. Чтобы получить замкнутую модель, необходимо ввести зависимость между напряжениями и деформациями. Такая связь называется определяющим уравнением.

Простейшим определяющим уравнением является закон Гука о = о(е). Согласно этому уравнению напряжение о зависит только от относительной деформации е и не зависит от пути нагружения и истории деформирования. Материалы и среды, которые могут быть описаны подобными соотношениями, называются упругими. Как указывалось выше, многочисленные наблюдения, проведенные в полевых и лабораторных условиях, показывают, что грунты не являются упругими и определяющие уравнения для них должны быть иными.

Определяющее уравнение для грунтов должно отражать отмеченную выше особенность грунтов - их жесткость при нагружении меньше жесткости при разгрузке. Поясним на простом одномерном примере, как можно решить эту проблему. Рассмотрим одномерную цепочку из грузиков, соединенных между собой пружинками. Возьмем какие-либо два соседних из них и пусть величины и 1 и и ₂ задают смещения этих грузиков из положения равновесия (второй грузик для определенности расположен правее первого грузика). Тогда разность и ₂ и 1 определит деформацию пружинки, соединяющей эти грузики. По закону Гука сила упругости, действующая на грузики, пропорциональна деформации о = к (и ₂ - и 1 ). Пусть при нагружении пружины ее коэффициент жескости равен к 1 , а при разгрузке он равен к ₂. При нагружении грузики сближаются и и ₂ - и 1

уменьшается, то есть производная по времени от d ( u-> и )

и₂ - и. отрицательна —^--- 11 <  0 . При разгрузке

• ^{2     1}                            d t

  д ( и 2 - и , )

  
  

  пружины, наоборот,

  
  

  d t

  
  

  > 0 . Чтобы учесть

  
  

различие коэффициентов жесткости при нагру- жении и разгрузке, вместо закона Гука следова-_                               6а , 6(u7 - u,)

ло бы писать соотношения = к ²  — при

6 t     ¹     6 t

6( u₇ - u .) „ 6а , 6 ( u₇ - u .)       6( u ₂ - u .) „

• -^-2---- <  0 и = к,    ---¹² при ²   — >  0 .

6 t              6 t     ²      6 t               6 t

Переходя к пределу сплошной среды, то есть увеличивая число грузиков и уменьшая расстояние между ними с сохранением плотности, разность u ₂ – u ₁ следует заменить на пространственную производную —, a ^{6( u 2 - u 1 )} заменить на

6x

• 6    6u 6 6u 6v„

  --=--= —, где v = — - скорость дефор-6t 6x 6x 6t 6x

мации среды. Тогда определяющие уравнения 6a , 6v переписываются в виде — = к 1 — при — < 0 и 6а ,6v      6v „ „51     6x

— = к2 — при — > 0. Эти два уравнения можно 61     6x записать в виде одного уравнения, если ввести

, ,             „ - k 2 + k 1 ,, _k 2 - k 1 _ коэффициенты p1 = 2 и p2 = 2 . Определяющее соотношение принимает теперь вид

6a    6 v

~ = ^P1 X. + P-2

6 1      6 x

6 v

6 x

Это уравнение содержит модуль производной скорости среды по координате и поэтому является нелинейным даже в малом, а сама зависимость между напряжением и деформациями представляется в виде уравнения эволюционного типа, связывающего скорость изменения напряжения и скорость деформации среды. Такой подход используется для описания поведения сред в теории гипопластичности [10].

Определяющее уравнение гипопластической среды в общем случае можно записать в виде

• ⁷    = Ц«> ) .,^a ) , + I , V .e К + N .V .e ) H I ,⁽³⁾

V - V где e =-----

V s

– пористость среды, V_s – объем твер-

6v,   6vj

—+- j

I 6x, дой фазы, V - полный объем, н, =  ---2-

( ^{6 v} _⁶ ^

–

^^^^^^e

6x, тензор скоростей деформаций, mi, =----2---- тензор скоростей вращений, Ц^] = 4tr (H) - норма тензора скоростей деформаций (аналогом ║ε║ в одномерном случае служит обсуждавшийся выше модуль v в уравнении (2)), L и N – не-6x которые тензорные функции указанных аргументов, имеющие различные представления, в которые входят константы, характеризующие свойства материала.

Не ограничивая по существу общности рассмотрения, обсудим плоскую волну, распро- страняющуюся в положительном направлении оси x. В этом случае искомые компоненты скоростей и напряжений являются функциями только одной координаты x и времени t. В соответствии с постановкой задачи рассмотрим распространение малых деформаций и, кроме того, будем считать, что начальное состояние среды однородное и v0 = 0 (индекс 0 здесь и далее соответ- ствует исходному невозмущенному состоянию среды). При сделанных предположениях система уравнений (1) и (3), описывающая движение гипопластической среды, приводится к системе трех нелинейных уравнений второго порядка для компонент скорости v = (v1,v2,v3)

6 ² v 1

^^^^^^s

2 62 v 62 v2      62 v k 6 н H c „—г = a > + a2 —7 + b hII , p 6x2     1 6x2     2 6x21

6 ² v ₂

^^^^^^s

2 62 v2      62 v      62 v36

c _s     г = a₃ —г + a    ³ + b H , (5)

-1 6x2     3 6x2     4 6x22

^^^^^^e

6 ² v 3

2 6 ² v₃      6 ² v       6 ² v_{2   k} 6

c _s2—y- = a ₅ —y- + a ₆ —y- + b    К , (6)

- 2 6x2       6x2      6x2      6x где

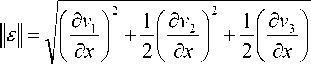
, а коэффи- циенты cp, cs1, cs2, a1,…,a6, b1,…,b3 определяют-

ся параметрами исходного состояния среды и принятой модели. Если все коэффициенты ai, bj равны нулю, то уравнения (4)–(6) превращаются в независящие друг от друга линейные волно- вые уравнения, описывающие распространение трех упругих волн (одной продольной и двух поперечных) со скоростями cp, cs1, cs2. Предполагая, что главные оси невозмущенного тензора напряжений σij совпадают с осями x, y, z, так что ax, = axz = <7^z = 0, получим вместо (4)-(6) более простую систему уравнений

6 ² v 1

^^^^^^e

2 62v,     , 6 ,, ,, cp —1 = bi— И, 6x     6x

6 ² v 2     7 6 ² v 2

c_v1         = 0,

6 1 ^{2       - 1} 6 x²

–

6 ² v 3

^^^^^^s

c. ^:, ^{5 p} V з = 0.

^{- 2} 6 x²

Уравнение (7) представляет собой нелинейное неоднородное волновое уравнение, описывающее продольные и поперечные движения среды, а два других уравнения (8) и (9) являются линейными волновыми уравнениями, как и в упругом случае, с постоянными, но, вообще говоря, различными скоростями cs1, cs2. Таким образом, две поперечные (сдвиговые) волны распространяются независимо друг от друга и от продольного движения, в то время как попе- речные движения воздействуют на продольные волны. Другими словами, в гипопластических средах поперечные волны приводят к возбуждению продольных волн. Применительно к нашей задаче это означает, что удары колеса о дно ко

рону x > 0 со скоростью, приближенно равной

c p , производные по x и t связаны соотношением

д д

— ~ — c „ — д t      p дx ’

и волновой оператор переписывает

леи в вертикальном направлении тем не менее будут вызывать продольные волны, бегущие параллельно поверхности.

Поперечные волны являются упругими и не приводят к появлению остаточных деформаций, поэтому сосредоточим внимание на обсуждении продольной волны и рассмотрим продольную волну в отсутствие поперечных движений ( v ₂ = v ₃ = 0). В этом случае продольные возмущения описываются уравнением

ся в виде

д ²    2 д ²      „ д (д дЛ

К _ д t2 pдx2      pдx(дt pдxJ

что позволяет уравнение (10) записать так:

. д (д д Л , д д v

2 c p —I — + c p — I = b-- ^p д x (д t ^p д x J    д x д x

Интегрирование этого уравнения по координате x дает уравнение первого порядка

д ² v    ₂ д ² v , д д v

—7 - с„ —7 = b-- д t ^{2 p} д x ²     д x д x

Здесь мы перешли к обозначению v = v , b = b. Решение этого уравнения зависит от знака про - д v          д v _                  2

изводной —. Если — < 0 всюду и b < c, то урав-дx       дx нение (10) сводится к линейному волновому

д v     д v   b

--+ c _p 1-- д t      д x 2 c_p

д v д x

= 0.

уравнению

Опишем характер решения этого уравнения. Пусть в начальный момент времени профиль возмущения имеет колоколообразный вид, что типично для возмущений, вызываемых ударами, ( x x 0 ) 2

д ² v

д t2

^^^^^^e

( c 2 - b^ = 0,

v ( x ,0 ) = v 0 e    ^{l 2}

.

и, как известно, его решения соответствуют переносу начального возмущения без и змене -ния формы с постоянной скоростью ^c i = c p - b . .

д v л

Если — > 0, то уравнение принимает вид дx

- ( c 2 + b )^ = 0 •         (12)

t                x

и его решения соответствуют переносу начального возмущения без измене ния формы с постоянной скоростью c ₂ = c p + b . В нашем случае b > 0, поэтому c >  c и профили, соответствующие по д v ложительным значениям градиента скорости —, д x распространяются быстрее, чем профили с отрицательным значением этого градиента. С учетом обсуждения, проведенного выше, это означает, что возмущения, соответствующие нагружению грунта, распространяются медленнее возмущений, отвечающих разгрузке грунта.

В предположении малости параметра b уравнение (10) можно упростить, воспользовавшись приближенным методом, изложенным, например, в [11]. Это позволит оценить остаточную деформацию, возникающую в среде после прохождения волны.

Факторизуем волновой оператор д2 _ 2 д2 =Гд_ AYA   AJ дt2 p дx2 (дt p дxJ(дt   p дxJ и выделим волну, распространяющуюся в положительном направлении оси x. Для любого волнового профиля, распространяющегося в сто

В начальный момент времени возмущение локализовано в окрестности точки x Произво-д v     „                            „ дная — для этого профиля меняет знак, поэтому дx с течением времени по мере распространения профиль возмущения будет меняться: участки с отрицательной производной движутся со ско-b ростью c = c--, а участки с положительной p 2cp                                b производной движутся со скоростью c 2 = cp + ~--.

2 c_p

В результате их взаимодействия амплитуда возмущения по мере распространения уменьшается и импульс через некоторое время исчезает. Если считать, что начальное возмущение сосредоточено в области (x0-1, x0+1), то импульс исчезнет, когда левая граница импульса догонит правую, то есть при выполнении условия x 0 — l + c 21 = x 0 +l + c t.

Отсюда находим время распространения импульса и дальность распространения

T = -22— = 2lc,,(15)

c 2 — c1

L = cpT = -lcp.(16)

Остаточную относительную деформацию среды § в точке x после прохождения волны можно найти следующим образом:

д u ( x , t ) г д ( д u) , г д ( д u) , г д v ( x , t )

5 = lim _t ^„         = I — I dt =    I — \dt =          dt .(17)

д x     • д t ( д x J    0 д x ( д t J    0 д x

Если до момента времени t через точку x про-dv ходят участки с отрицательной производной , то согласно (14)                             dx dv     1 dv

— _---.

d x    c 1 d t

После момента времени t через точку x проходят участки с положительной производной и d v _ 1 d v d x    c 2 d t

Подставляя эти выражения в (17), находим , ff 1 s v К to f 1 5 v К     1 / ч 1 / J 1 1

5 _ I---I dt + I---I dt _ v ( x , t ) +— v ( x , t ) _|--- I v ( x , t )

,                          ,                                           ,.

0 I c 1 ⁵ t ) , I c 2 ⁵ t )         c 1            c 2            I c 2 c 1 )

Как видим, остаточная относительная деформация отрицательна, что соответствует остаточному сжатию среды.

Таким образом, остаточную относительную деформацию на расстоянии r от точки x0 по направлению распространения сигнала можно оценить величиной r2

|5 _ IIvо e L2 ~ "Г vо e L2.(18)

\ c2 c1)

Оценка (18) получена для случая плоского возмущения. Проведем теперь на ее основе оценку уплотнения почвогрунта в боковых полосах трелевочного волока, возникающего под воздействием динамики движения и поворота лесозаготовительной машины. Удар колес о грунт вызывается неровностью рельефа волока, столкновениями колес с боковыми стенками колеи при движении и поворотах. Удары характеризуются коротким импульсным воздействием и создают как продольные, так и поперечные волны. При этом преобразование энергии воздействия в колебательную энергию распространяющихся волн происходит в некоторой пространственной окрестности вокруг точки воздействия, и эта область также принимает участие в излучении волн. Приближенно вне этой области источник воздействия можно описывать моделью сферического излучателя, расположенного на поверхности [2]. Эффективный радиус излучателя обозначим R0. Энергия возмущения вдоль поверхности переносится главным образом поверхностными волнами, объемные волны во внимание можно не принимать [2]. Скорость распространения поверхностных волн в однородной среде [2] практически не зависит от частоты, но поверхностные волны экспоненциально затухают вглубь на расстояниях порядка длины волны. Поэтому оценкой (18), полученной в предположении отсутствия дисперсии, можно пользоваться непосредственно вблизи поверхности. Толщину этого слоя можно оценить величиной cδt, где c – скорость распространения волны, а δt – длительность импульса. Для типичных скоростей поверхностных волн в почвогрунтах ≈300 м/с и при длительности импульса 5 мс толщина слоя будет более 1 м, что превосходит представляющий интерес почвенный слой ≈0,4 м.

Отметим еще чисто геометрическое затухание возмущения, вызванное тем, что от места воздействия возмущение распространяется по всем направлениям. Можно принять, что в результате геометрического затухания поверхностной волны амплитуда скоростей точек среды убывает 1

как   , где r – расстояние от места удара до точ- r ки, в которой определяется остаточное сжатие. Удары, вызывающие волны деформаций в среде, можно считать происходящими случайно и охарактеризовать их средним числом ударов на единицу пути n _1, где a - среднее расстояние a между двумя последовательными ударами. Для оценки полного остаточного сжатия среды Δ нужно просуммировать сжатия (18), вызывае- мые всеми ударами

R + x

A_ to j n5\dx ~ J

-to

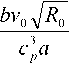
e ^{L 2} dx

V R ² + x²

Здесь интегрирование проводится по трассе, R – расстояние до трассы от точки, где определяется остаточное сжатие, L – дальность распространения сигнала (16), v0 – максимальная скорость точек среды при ударе, определяемая на нормировочном расстоянии R0 от места удара. Скорость v0, определяемая силой удара, зависит от многих факторов: скорости движения лесозаготовительного агрегата, его нагруженности, неровности рельефа волока, характера движения, давления в шинах. Исследуя влияние ско- ростного режима движения лесозаготовительной машины на уплотнение почвогрунта, можно принять, что в среднем скорость v0 при прочих равных условиях пропорциональна скорости движения транспорта v, то есть v0 = αv. Значение числового коэффициента α определяется перечисленными выше факторами.

В результате, выполняя интегрирование и подставляя выражение (16) для дальности L, получаем оценку среднего уплотнения почвогрунта на расстоянии R > R0 от трассы волока при движении по нему лесозаготовительной машины со скоростью v

v

A _ 4a— cp

¹ 1² R о f f R a ² L^J ( L

Функция f ( s ) _

e -^{( s 2 + x 2} ) dx

4/ a2 + x2 ’ to

J

входящая в (19),

является монотонно убывающей. Ее значения не превышают 2 и почти равны 0 при R > 2 L .

Pl/

/ P

= 1 + A

.

В окончательном выражении для остаточного сжатия соотношение (19) нужно еще умножить на число проходов транспорта по трассе I

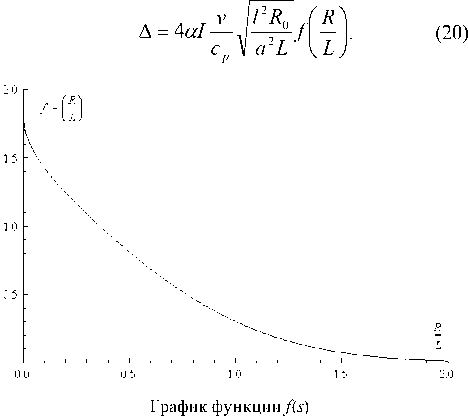
Приведем числовые оценки. Сейсмические волны распространяются в Земле со скоростями 2–8 км/с. В рыхлых породах скорости могут опускаться до значений 1 км/с и меньше. Кроме того, вдоль поверхности волны распространяются с меньшими скоростями, чем в толще Земли [2]. С учетом этого в качестве оценочного значения скорости c_p можно взять 300 м/с. Для параметра b , характеризующего отличие скоростей распространения деформаций нагружения и разгрузки, примем 10⁴ м²/с², тогда относительное отличие указанных скоростей составит 10 %. Характеристику удара l положим равной 20 см, при этом дальность L распространения импульса плоской волны (16) составит 4 м. Среднее расстояние между двумя последовательными ударами оценим в 0,5 м. Для R ₀ можно принять 1 м [2]. Подстановка этих значений параметров дает для остаточного сжатия

Отметим, что оценка (20) не учитывает изменения свойств грунта при многократном прохождении по трассе транспорта и потому является завышенной. Отметим также, что оценка уплотнения почвогрунта (20), как это следует из проведенного рассмотрения, применима на расстояниях R больших R0. На расстоянии R = R0 уплотнение конечно и быстро убывает с увеличением расстояния R.

Используемый в литературе [5] коэффициент уплотнения почвогрунта ным образом

P1/ / P

связан с Δ очевид-

A» 2 - 10 - 3 O f | - |.

I 4 )

Для предельных скоростей движения лесозаготовительных машин примем: 4,5 м/с для порожнего прохода и 2,5 м/с в груженном состоянии. В свою очередь, коэффициент α для груженных машин, очевидно, больше, чем для порожних. Как видим, после 50 проходов транспорта уплотнение почвогрунта на расстоянии 2 м от трассы волока составит от 1 до 10 % при α = 0,1 ÷ 0,5. Для расстояния R = R ₀ результаты получаются в 1,5 раза выше.

* Материалы данной статьи получены при выполнении НИР № 01201255482 «Разработка теоретических основ сквозных технологических процессов и модульных систем машин лесозаготовительного производства».