Математическая модель управления надежностью как компонент системы поддержки принятия решений в деятельности силовых ведомств

В современных условиях ухудшения криминогенной обстановки для обеспечения качественной поддержки принятия решений должностными лицами силовых ведомств необходима разработка соответствующего программного обеспечения специального назначения. Особую актуальность данная задача приобретает в области технического обеспечения, в том числе при организации охранной деятельности на объектах особой важности, требующей поддержания на необходимом уровне технических служб исправным охранным оборудованием, готовым к применению по назначению [1; 12].

Автоматизированные системы поддержки принятия решений (далее – СППР) специ ального назначения обладают высоким потенциалом в пов ышении оперативности управ © Царькова Е.Г., 2022

Царькова Евгения Геннадьевна кандидат физико-математических наук, научный сотрудник НИЦ-1. Научно-исследовательский институт Федеральной службы исполнения наказаний, Москва; доцент кафедры информационных систем и методов искусственного интеллекта. Тверской государственный университет, город Тверь. Сфера научных интересов: методы оптимизации; математическое моделирование; оптимальное управление; нейросетевые технологии. Автор более 100 опубликованных научных работ.

ления техническим обслуживанием (далее – ТО) оборудования, а также позволяют получать обоснованные рекомендации при принятии управленческих решений за счет реализации в таких системах функций прогнозирования, оперативного управления, контроля, принятия решений и др. [4; 7]. Деятельность силовых ведомств в части мероприятий по техническому обеспечению требует разработки математических моделей и методов для подобных СППР, обеспечивающих лицо, принимающее решения (далее – ЛПР), достоверной и объективной информацией об оборудовании, с возможностью дальнейшей адаптации к развитию и расширению системы [5; 10; 13].

Важным компонентом рассматриваемого класса СППР является модуль управления надежностью технических средств. В настоящее время в подавляющем большинстве случаев замена и ТО охранного оборудования осуществляется либо по факту его отказа, либо с учетом сроков, закрепленными нормативно, в соответствии с рекомендациями производителя. Вместе с тем для снижения финансовых затрат на проведение ТО с сохранением необходимого уровня надежности и целостности оборудования перспективным является разработка и применение методов управления надежностью исходя из результатов оценки его технического состояния, что позволяет обеспечить баланс между требуемым уровнем надежности и объемом финансирования на его поддержание за счет своевременного проведения ТО. Применение предиктивной аналитики, управления по техническому состоянию, основанному, в том числе, на математических моделях надежности, позволяет выявить неисправности оборудования на ранних стадиях, обеспечивая его готовность к использованию и снижая продолжительность внеплановых простоев технических средств [3; 6; 8; 11].

Модель эксплуатации технической системы

В деятельности технических служб силовых ведомств при работе с крупным парком технических средств непрерывно возникают задачи ремонта и замены оборудования, связанные с его устареванием, изнашиванием и, как следствие, снижением эффективности (см. Рисунок 1).

На Рисунке 1 точками t_{p 1}, t_{p 2},..., t_pn отмечены моменты времени, в которые осуществляется ремонт технического объекта, в результате чего эффективность использования оборудования повышается до величин E 1 , E 2 , ..., E n ; t_зам - момент замены оборудования.

Построим модель эксплуатации нерезервированного технического объекта (системы), относительно которого проводится периодическое техническое обслуживание. На смену состояний объекта влияют потоки отказов и восстановления, которые являются пуассоновскими и независимыми, тем самым в технической системе обеспечивается про-

Математическая модель управления надежностью как компонент системы поддержки ...

текание марковского процесса, где экземпляры оборудования – объекты с дискретными состояниями и непрерывным временем.

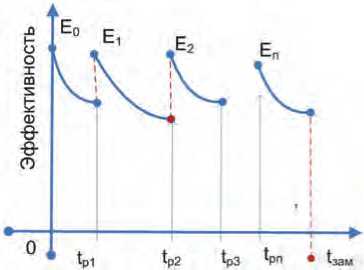
Рисунок 1. Изменение эффективности оборудования в течение времени

На Рисунке 2 приведен ориентированный граф состояний рассматриваемого технического объекта.

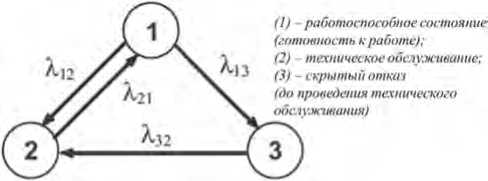
Рисунок 2. Вид графа состояний объекта с периодическим техническим обслуживанием

Введем обозначения: t_TO - периодичность ТО; t_to - продолжительность проведения

ТО для устранения неисправности; u(t) =--- - частота проведения ТО, установленная на момент времени t е [0, T].

Тогда в соответствии с графом состояний значения интенсивностей переходов [12]

^А 2 = /^ , Л э = ^А , ^ 23 = И- •

/ tTO

В соответствии с графом состояний технической системы получаем следующую систему дифференциальных уравнений [2; 9; 14]:

dP 1 (t) dt

^^^^^^»

А +--I P1(t) +--P2(t), too)

dP, (t)     1     . x 1     . x 1 + AtTO.

^  2,  =—Pi(t)--P2(t) + ^TT° P3(t), dt    tTO       Too        At TO dP3(t) dt

= APi(t) - 1^^ P,(t), At TO где P/(t) + P2(t) + Рэ(t) = 1; P/(0) = 1; P2(0) = P,(0) = 0.

На Рисунках 3–5 приведены графики значений финальных вероятностей, полученных в соответствии с (1), при 2 = 10 5 ,тто = 0,5.

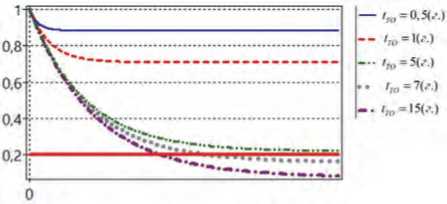
Рисунок 3. Графики P ₁( t )

0,00014

0,00012-

0,0001- ■

0,00008- ■

0.00006 '

0,00004 ■

0,00002

о< о

— /,„=0.5(г.)

--'т-Кл)

• —    /го = 5(л)

• • • 'ГО-7(Л)

• - • <Ю-1$(А)

Рисунок 4. Графики P ₂ ( t )

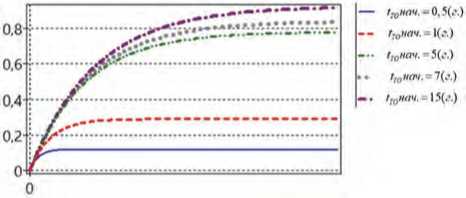
Рисунок 5. Графики P ₃ ( t )

В ходе периодического изменения t_TO от t _TOHa4 до t_TO max ставленные на Рисунках 6–9.

получаем результаты, пред-

Рисунок 6. Графики P ₁( t )

Математическая модель управления надежностью как компонент системы поддержки ...

0.00044г

0,0003

0.0002

0,0001

Рисунок 7. Графики P ₂ ( t )

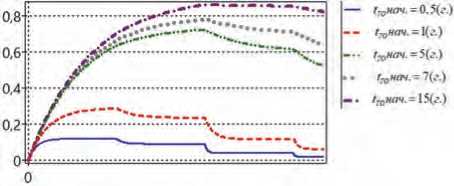
Рисунок 8. Графики P ₃ ( t )

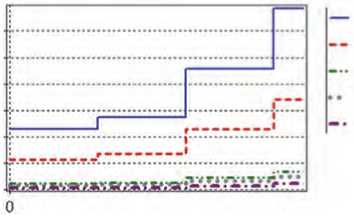
Г_гоноч. -0.5(г.) г_го*оч.=1(г.) г_тнач. =5(г.) t_roHO4. = 1^

/го*от. = 15(г.)

Рисунок 9. Графики изменения t_TO в течение периода наблюдения

Таким образом, при определенных значениях параметров системы, в частности при изменении периодичности, вероятность безотказной работы не снижается ниже критического уровня. При увеличении частоты ТО надежность технической системы повышается, таким образом, возможна постановка оптимизационной задачи управления надежности в условиях наличия ограничений финансовых ресурсов, направляемых на проведение ТО.

Задача оптимального управления надежностью технической системы

Рассмотрим задачу оптимального управления надежностью ТС, выбрав в качестве управляющего параметра периодичность ТО t_TO = u ( t ) , t е [0, T ] и используя следующие обозначения:

x 1 (t) = P1 (t), x2 (t) = P2 (t), x3(t) = P3 (t), u(t) = —, t е [0, T], Ц = —, tTO                 TTO .         (2)

X 1 (0) = P 1 (0) = X ⁰ , x 2 (0) = P 2 (0) = X 2 , x 3 (0) = P 3 (0) = X 3 ⁰ , u (0) = Y ⁰

Целью управления является минимизация затрат на проведение ТО при условии сохранения значений показателя надежности (состояния готовности) не ниже заданного уровня a : x 1 ( t ) >  a , t e [0, T ] , которое может быть учтено в задаче путем ввода штрафного коэффициента М .

Приходим к задаче оптимального управления следующего вида.

Требуется минимизировать функционал

T

I(и) — J(ae 5tx2(t) — Nx1(t) + Mmax2 {a—x1(t);0})dt при динамических ограничениях:

X 1 —— (l + и (t)) x 1 (t) + M X ₂(t) , t e [0, T ] ,

•         1 2, x , x Г , x 1 2, x) , x Г 1 , x .)

x 2 —— и (t) x_y (t) — M + и (t) + и (t) x ₂(t) +     u (t) + 1 и (t) , t e [0, T ]

2          V 2    )      1 2      )

с начальными условиями x1 (0) — X 0, x 2 (0) — X 0, и (0) — Y0, при ограничениях на управление

0 <  и ( t ) <  Y max, t e [0, T ] .

Здесь а - стоимость работ по техническому обслуживанию объекта в единицу времени; д >  0 - дисконтирующий множитель; N >  0 - весовой коэффициент.

Численный метод решения дискретной задачи оптимального управления

В ходе исследования разработан алгоритм численного решения задачи. Построим дискретную задачу оптимального управления. С использованием явных разностных схем [6; 11] выполняем дискретную аппроксимацию. Введем на отрезке [0, T] равномерную сетку c шагом A t — Tq :{ t i —A t ■ i ,0 <  i <  q } . Введем обозначения: x 1 ( t i ) — x 1 , x ₂( t i ) — x 2 , и(t i ) — и , i — 0, q .

С использованием формулы Эйлера 1-го порядка точности аппроксимируем производные:

i x 1

x 1 ( t ) — —

—

A t

x _{1          i}x ₂

, x 2 ( t ) —— ■

—

A t

i x2    000000

, i — 0, q 1 , X i — X 1 , x 2 — X 2 , и — Y .

Дискретная задача оптимального управления, аппроксимирующая исходную с точностью O ( A t ) , примет следующий вид:

q ^{— 1}

I (u) — ^ ( a e ^{— 5 t} x ₂ i — Nx 1 i + M max²{ a — x 1 i ,0} ) A t ^ min , i — 0

x 1 i ^{+ 1} — x 1 i + A t ( M x ₂ i — ( 2 + и ) x 1 i ) , i — 0, q — 1 , ,+1 i / 1 / , Л² , Г , 1 / , \² ) , Г 1 , .) i x₂    — x ₂ +A t — и   x, — M + и + и    x-. + и + 1 и

, i — 0, q — 1 ,

• 2     2    ( X ’ 1 ( X ’ J 2 12 J

x 0 — X 0 , x 00 — X 2 ⁰, и ⁰ — Y ⁰ , 0 <  u ⁱ <  Y max , i — 0^ .

Математическая модель управления надежностью как компонент системы поддержки ...

Функция Лагранжа имеет вид

L (x, c , u ,

q ^{- 1}

P ) = ^( a e-^{s t} x 2 ⁱ

i = 0

- Nx 1 ⁱ + M max² { a - x 1 ⁱ , 0} ) A t +

q ^{- 1}

+ ^ p 1 ^{i + 1} ( x 1 ^{i + 1} - x 1 ⁱ - A t ( ц x 2 ⁱ - (l + u ) x 1 ⁱ ) ) +

i = 0

q - 1

+Z P 2 i i=0

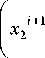
i

^{- x} 2

ii    i   i   iii

• -At - u X] - ц + u + u x3 + u +1 u

I X ’ 1 V X ’) 2 IX )

Используя условия стационарности функции Лагранжа

-⁽ x , c , u , p ) = 0,

О ^X 1

----( x , c , u , p ) = 0, i = 0, q , получаем рекуррентные соотношения: d x ₂ ⁱ

P i i = P i i ^{+ 1} ( 1 ^-A t ^{(l + u}i ) ) + P 2 '

p 2 i = P 2 i ^{+ 1} ( 1 + Ц - A t ( X + u

( ui ) 2                                ₍ i.

———+ A t ( N - 2 M max { a - x 1 ,0

i + 1 ( ^u' ) 2                                              i

—X —+A t ( N - 2 M max { a - x 1 ,0 } ) , 0 , q - 1 , p ₂ ⁴ = 0 .

, 0 , q - 1 , P i ^q = 0 ,

Вычисляем производные по направлению:

—- = p 1 ^{i + 1} x 1 ⁱ A t + p ₂ ^{i + 1} A 1 1 — ( x 1 ⁱ - x ₂ ⁱ + 1 ) u - x ₂ ⁱ + 1 I , i = 0, q - 1 . d u                   v X

На основе соотношений, полученных из условий стационарности функции Лагранжа, с применением метода проекции градиента построим приближенное решение задачи. В используемом численном методе фазовые ограничения учитываются путем ввода штрафных функций. Для реализации алгоритма построения численного решения задачи автором разработано настольное приложение в среде Lazarus, реализующее метод градиентного спуска. В ходе исследования построена блок-схема алгоритма численного оптимального решения задачи (см. Рисунок 10).

Заключение

Разработанный алгоритм может быть использован при построении системы поддержки принятия решений для управления надежностью охранного оборудования, а также для прогнозирования надежности технических систем, обеспечивая возможность перехода технических служб от планового технического обслуживания к обслуживанию по состоянию и снижая издержки при управлении техническим обеспечением специального назначения [15].

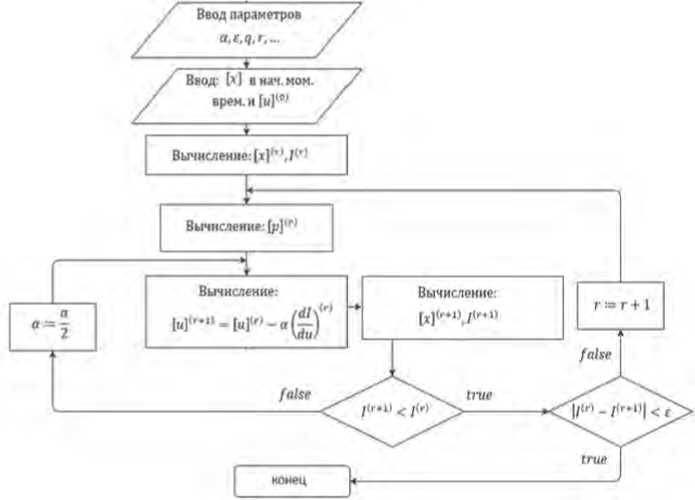
Рисунок 10. Блок-схема алгоритма градиентного метода решения задачи