Математическая модель управления производственными мощностями лесотранспортного предприятия

Функционирование лесотранспортных предприятий требует учета природно-производственных условий лесозаготовок, при которых в течение небольшого временного интервала нужны транспортные средства различных классов, в частности, при организации многоступенчатых перевозок, связанных с особенностями производственного процесса и качеством автомобильных дорог [3; 198]. Поэтому представляет интерес задача оптимального использования производственных мощностей и инвестиций как во временной развертке, так и в плане структуры автотранспортного предприятия.

Допустим, что лесопромышленное предприятие имеет на балансе парк лесовозных автомобилей одного типа и периода эксплуатации. Перед руководством предприятия возникает проблема инвестирования денежных средств в парк лесовозных автомобилей, то есть вопрос о том, в какой период времени и в каких количествах необходимо вкладывать денежные средства для эффективной работы предприятия.

Для t = 0, 1, …, T положим D_t – прыбыль предприятия за период t ; w_t – мощность парка машин в период времени t в денежном выражении; I_t – инвестиции в начале периода t , то есть приращение мощности парка, I _Σ ⁼ ∑ I_t – суммарные t = 1

инвестиции за «большой период» T , I = ∅

Положим, что мощность парка w_t через один период в результате амортизации принимает значение w_t ⋅ ρ , где ρ < 1 – коэффициент, постоянный для данного парка машин. Тогда с учетом инвестиций мощность парка в период t + 1 составит величину w_{t + 1} = w_t ⋅ ρ + I_{t + 1}. Зависимость дохода предприятия в период t от его мощности зададим уравнением вида

D t ⁽ w t ) = a t • w t - Э- w t ,           (1)

где αt и β – некоторые вещественные положительные коэффициенты. Причем первый из них зависит от периода t. Из (1) следует, что вначале с ростом мощности прибыль от основной хо- зяйственной деятельности растет, затем темпы αt роста снижаются. Наконец, при wt =     при-

2 •e быль достигнет максимального значения, и дальнейшее увеличение мощности приведет только к снижению прибыли (см. рисунок). Последнее связано с действием известного экономического закона убывающей доходности: по мере увеличения затрат одного типа при фиксированных всех остальных затратах в некоторый момент будет достигнута точка, за которой предельный результат производства будет уменьшаться [1; 140]. Следовательно, при фиксированных постоянных издержках прибыль с некоторых пор будет снижаться.

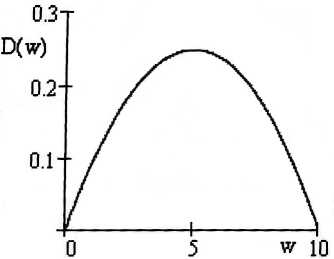
Зависимость дохода предприятия от производственной мощности

Как было замечено выше, α_t зависит от t . Таким образом, мы можем учесть в модели сезонный характер работ, когда эффективность производственных мощностей зависит от временного периода. Учитывая амортизацию и инвестиции I_t , проведем последовательность подстановок в формулах w_{t + 1} = w_t ⋅ ρ + I_{t + 1}.

W 1 ^- w о • ^р + I 1

w 2 ^- w 0 • Р + 1 1 • ^р + 11

W 3 ^- W 0 • Р + I 1 • Р + I 2 • ^р + I 3

T . , T-1. , T - 2 .          . , wt - wо• Р +I1 • Р +I2 • Р + '" + It.

То есть w t ^- w о • р ' + Е I i • р ' * . Теперь мы мо-

* - 1

жем сформулировать задачу оптимального использования инвестиций в виде:

T

Е Dt ^ max t - о

T

^Е I t ^- I к .

t - 1

Мы не будем предъявлять требование неотрицательности инвестиций, поскольку отрицательные инвестиции иногда можно трактовать как продажу мощностей или сдачу их в аренду. Найдем максимум функции

T        ( TА

F ⁽ I 1 , I 2 ,'" , I t , ^{X ) -Е} D t ^{- X} ’l ^Е I t ^- 1 к I , (3)

t - о         11 - о где (          t         А     (         tI

Dt-at '| wо• р + ЕI*• р *|-Р- wо-р + ЕI*•р * , к           *-1         V      V          *-1

X - множитель Лагранжа. Здесь мы учли условие I о = о.

Тогда д в £ £А _ л - о, где j = 1, 2, ., T.(4)

d Ij t Ео - Ij t J I               2 • t j                     2 • t* J I

' D t _-\ a _t ■ Р - 2 • в Aw о • Р     + Е I * ■ Р        I • если] ^t.

5I                         V               *-1

j ^                           о , если j >  t .

Подставив значения частных производных прибыли в уравнение (4), после ряда преобразований получим систему уравнений

1 T      t - j

Tt

ЕЕ I*- р 2t - *- j t - j*-1

^-Т^' ^Е а'^{Р -}

² • p t - j

T1 w о • Е р   -ppy X t - j          2 • р для j = 1, 2, ..., T. Запишем систему в матричной

форме.				1 " Е^ в				— • X-E . 2 • в
			R • I		• A - w o		P -			(5)
I -	Здес ( 1 1' I 2 ■	ь ,	A -	( T Е a t t - 1 T Е a t t - 2	t - 1 Р t - 2 Р	, ’	P -	( T T 2 - t - 1 Е р t - 1 T T 2 - 1 - 2 Е р t - 2	• E -	1 : ■
	V I t V							T		V 1 V
				V « t v				V Р V

а матрица

	( т -1 T ■ 2- j Е р	T - 2 _ . 2 " j р- Е р •	T - 1 • р
	j - о	j ' - о
R -	T - 2 , . 2 - j р- Е р	T - 2 , . 2 j Е Р	.  рт - 2
	J "	j - о
	T - 1 V р	T - 2 Р	1 V

Таким образом, элементы матрицы R опреде ляются равенством т -1 _ .

Е 2 ‘ * р , * - о

если j = t

t - j

Р

R j , t ^-1

j - t

Р

T - 1 ,

• Е Р

* - о т - j

• Е р

* - о

2 . *                    . .

, если j < t .

-² * , если j > t

Матрица R при любом значении T обладает следующими свойствами:

1. Определитель матрицы | R | = 1.
2. Обратная матрица
	( 1	- Р	о "	о I
	- Р	1 + Р 2	- Р "	0
R - 1 -	0	- Р	1 + Р 2 •"	0
	V о	0	о •	1 + Р 2 у

Таким образом, несмотря на довольно сложное описание матрицы R , ее обратная матрица имеет очень простой вид. Доказательство мы опустим, не желая чрезмерно увеличивать объем статьи. Заметим только, что оно ведется по индукции и опирается на свойства блочных матриц [2; 55-56].

Умножим левую и правую части уравнения (5) слева на R ^-1:

I ^-       • R ' • A ^- w o ' R ■ ^{P -}Т”д • ^' R ¹ • E .    ⁽⁶⁾

2 • p                            2 • p

Умножим матрицу R ¹ на векторы A , P и E :

		1 - р
а 1 - 1 .      а 2 - р ' а 1 R • A -	р , R - 1 • P - ° и R "1 • E -	( 1 - Р ) 2
V « t - р - а т - 1 v	• • • V о V	( 1 - Р ) 2 V 1 - Р + Р 2 V

Просуммировав члены уравнения (6) по стро-

кам, получим:

[л—^ Р + ^L + ^ • ( - л )

1 ¹      w ^о       2 • в 2 • в ^v ’

- а ^{2 - Р}- « 1 + ( ^{1 - Р )} 2 • ( - _Л )

²        2 • в 2 • в '   '

I t - 1

I t ^-

- ат-1- Р' ат - 2 +(1- Р)2

2 • в 2 • в а т ^{- Р}' а т - 1 + ^{( 1 - Р +} Р )

2 • в           2 • в

•^{( - л )}

•^{( - л )}

Таким образом, мы нашли значения инвестиций в периоды t = 1, 2, …, T , выраженные через λ . Теперь просуммируем соответственно левые и правые части равенств (7).

T

2 I t = I £ = - w 0 • ^p + t =1

T -1

^{( 1 -} P ) • S a t + а т

___________ t =1 ____________

2 • в

-

Далее, повторив все выкладки предыдущего пункта отдельно для каждого класса машин, получим систему уравнений, в которой значения I_{m , t} аналогично (7) выражены через множитель Лагранжа λ . Просуммируем соответственно левые и правые части (7). Тогда

MM

I £ = - 2 G m + S H m • ² ,          (9)

m = 1      m = 1

-

( T - 1 ) ^ ( 1 - p ) ² + 1 , 2 .

2 • в

где

Отсюда т-1

² • P\I z + w о • ^{p ) -( 1 - p} ) • S a t ⁺ а т

- ² =------------7--^=1 •

( T - 1 ) . ( 1 - p ) ² + 1

Теперь, подставив значение – λ в (7), мы можем найти оптимальные значения инвестиций I_t .

Пример. Пусть количество периодов T = 10, исходная мощность в денежном выражении w₀ = 5, коэффициент в уравнении (1) β = 0,01, ρ = 0,95, I _∑ = 50. Значения коэффициента α_t для различных периодов времени приведены ниже в таблице. Также в таблице приведены соответствующие расчетные значения инвестиций, производственных мощностей и дохода.

G m   w m ,0 ’ ^p _m

Отсюда 2 =

(        \ t - 1

(1 - pm )• Sam, t + am, T t=1

² • в

m

^{( T} - 1И^{1 -} p m ^{) 2} + ^{1 2} • P m

M

I £ ^{+ 2} G m

_____ m = 1

M

2 H m m =1

Подставив λ в уравнения (7), получим систему уравнений, определяющих величины инвестиций для всех классов машин m = 1, 2, …, M за все рассматриваемые периоды времени t = 1, 2, …, T .

I m ,1

„ , ^am ,1 ^{-( 1 - p} m ) • ²

^- w m ,0 • ^p m ⁺----- 277;------

^P m

Пример расчета инвестиций за 10 периодов времени

1	2	3	4	5	6
Период t	αt	ρt	Инвестиции It	Мощность wt	Доход D t
1	0,2	0,950	4,944	9,694	0,999
2	0,2	0,903	0,485	9,694	0,999
3	0,2	0,857	0,485	9,694	0,999
4	0,4	0,815	10,485	19,694	3,999
5	0,5	0,774	5,985	24,694	6,249
6	0,5	0,735	1,235	24,694	6,249
7	0,7	0,698	11,235	34,694	12,249
8	0,8	0,663	6,735	33,694	15,999
9	0,9	0,630	6,985	44,694	20,249
10	1,0	0,599	1,428	43,888	24,626

Рассмотрим следующую задачу, в которой автомобильный парк делится на M классов лесовозных автомобилей. В каждом классе представлены машины одного типа и времени эксплуатации.

Аналогично (4) найдем

MT Bq

^ = s s Dm . _ x = о, где j = 1 2, _ T dIm,j m=11=0 dIm,j

I m ,2

I m , T

^a m ,2 ^p _m • ^a m ,1

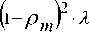
2 •P

m

a m , T ^- p m • a m , T - 1 ^-l ^{1 -} p m ^{+ p} m

2 • P

m

В приведенном выше примере все оптимальные значения инвестиций положительны. Однако при других исходных данных могут получаться и отрицательные значения I_{m t} . Если под I_{m , t} >  0 понимать любые привлечения мощностей в основную производственную деятельность предприятия, а под I_{m t} < 0 – любой способ их изъятия, то такое решени^, е может быть впол-

не адекватно исследуемому процессу.

Разумеется, адекватность модели зависит не только от самой модели, но и от цели и объекта

исследования. Мы допустили ряд упрощений, которые позволили получить выражения I_{m t} в общем виде. Такое представление результа^, та позволяет проводить дальнейшие исследования

аналитическими методами.