Математическая модель устройств на базе напряженных магнитоанизотропных структур

В настоящее время разработано множество разнообразных функциональных устройств на базе НМАС: модуляторы, ключи и переключатели, преобразователи перемещения, регулируемые линии задержки, преобразователи силы и крутящего момента [1, 2], ключевые элементы [3] и акселерометры [4, 5].

В качестве базовой схемы перечисленных функциональных устройств используется компенсационная резонансная схема измерения, в которой чувствительный (ЧЭ) и компенсационный (КЭ) магнитные выполнены на кольцевых ферритовых магнитопроводах (рис. 1).

На ЧЭ 1 и КЭ 2 элементах расположены обмотки возбуждения 4, 5 и измерительные обмотки 3, 6. Обмотки возбуждения 4, 5 включены пос-

Рис. 1. Компенсационная резонансная схема

ледовательно-согласно и питаются от генератора синусоидального напряжения 7. Измерительные обмотки 3, 6 соединены последовательновстречно и подключены к выходу измерительного прибора 9. Параллельно обмоткам 3, 6 включен конденсатор 8, образующий совместно с обмотками резонансный контур. При отсутствии усилия Р сигнал на выходе измерительного прибора 9 равен нулю. При давлении силы Р в кольцевом ЧЭ 1 возникают механические напряжения, которые приводят к изменению его магнитной проницаемости. При этом увеличивается разностный сигнал на выходе измерительных обмоток 3, 6. Выходной сигнал достигает максимума при максимальном усилии P = P max . Дальнейшее увеличение силы Р уменьшает выходной сигнал.

Физическая модель ферромагнитного ЧЭ представлена в виде четверти кольца на рис. 2, где P – сила воздействия на кольцо; a = Г н — Г в - ширина кольца; r н , r в – наружный и внутренний радиус

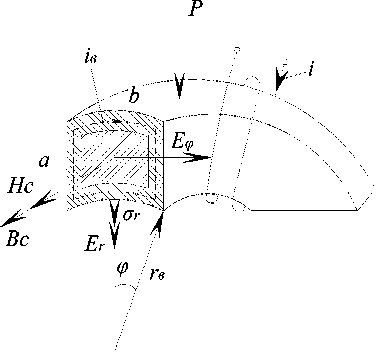
Рис. 2. Физическая модель ЧЭ кольца соответственно; b – толщина кольца;

г - г r0 = —^— -средний радиус кольца; ф - угол между осью и радиусом; Er.Еф - напряженности электрического поля на гранях сечения; BC – магнитная индукция внешнего электромагнитного поля; H C – напряженность магнитного поля по поверхности сечения кольца; i – ток, протекающий через обмотку возбуждения; iв – вихревой ток.

Математическая модель ферромагнитного ЧЭ НМАС описывается уравнениями теории электромагнитного поля, ферромагнетизма и упругости. Решение этой модели в трехмерном пространстве связано с большими трудностями. Поэтому задача была сведена к двумерной и решена в полярных координатах. При этом принимается ряд следующих допущений:

• 1.    Магнитная индукция B С внешнего электромагнитного поля, в котором находится ЧЭ, изменяется по синусоидальному закону.

• 2.    Магнитное поле равномерно и имеет только нормальную составляющую магнитной индукции B С .

• 3.    Комплексная магнитная проницаемость ^Д зависит от значения механической силы P,

• 4.    Плотность токов S r , 8 ф по толщине кольца не изменяется, что имеет место при b /(2 А ) <  0.5 , где А - эквивалентная глубина проникновения электромагнитного поля в кольцо.

• 5.    Тангенциальные составляющие напряженностей электрического поля E r и E ^ на гранях сечения кольца постоянны.

• 6.    Поля выпучивания, идущие в обход сечения кольца, относятся к полям рассеяния.

• 7.    Механическая сила Р (напряжение у) направлена по радиусу кольца под прямым углом к магнитному полю B С .

• 8.    Среда структуры кольца анизотропна или изотропна.

Е_ст = f ( P ) .

При принятых допущениях в двумерном пространстве при одновременном воздействии силового поля и электромагнитного поля возбуждения состояние ЧЭ описывается дифференциальными уравнениями в полярных координатах.

д нС - a r	у ф Е ф ;	(1)
a H с . -ф	= У гЕг ;	(2)

аBe   1 аBe аHC _ a hc B2 a hc -a Да; (4)

a wr

^E a r? =                ⁽⁵⁾

где У _г , У ф - удельные электрические проводимости по направлениям; E r , ^Е_ф , H c - комплексы действующих значений напряженностей электрического и магнитного полей по поверхности сечения кольца по переменным г, ф и с; с = 2- Л Г о = const - длина кольца; г ₀ - средний радиус кольца; to - круговая частота; Д_а - магнитная проницаемость от механического напряжения a , w r - перемещение точки структуры по радиусу r; E – модуль упругости.

Граничные условия при этом имеют вид (рис. 2).

H c ( г , ф ) = H c ( г ) при г = г в + b / 2, ф = 0 ;

Г в <  r <  Гн ;                (6)

H c ( ф , r ) = H c ( ф )

bb при - arcsin---< ф < arcsin—, 2r             2r вв при малых углах ф

ф 2

b = L = j Г0 dф ф1

b

H С ( г , ф ) = 0 при ф = ^{+ arcsin} . ^{2 г}в

H с ( ф , r ) = 0 при r = г в + b /2 .     (8)

Из уравнений (1) и (2) следует:

E = ±a H c . E = ±5 H c

• ^ф у_ф a г    ^г у _г aф • ⁽⁹⁾

Уравнений (9) подставим в уравнение (3).

1 a2 H с 1 а2 Hc = - jtoEaHC -ф2 уф а г2 Уг HC 1   а2 hc =    .           7 + Уг]ЮДп -ф2 1    -2 Hc Уф)юцп - г2 где % г  уУгНДО.. Хф ^фрН^От .

Тогда совместное решение системы уравнений (1) – (5) дает:

a Er - еф aг -ф

а BC a t

- jtoVaHc;

²н„ а²Е„

H С =^=S^-^ С = H c ( г, ф ) ₊ H c ( ф , г ), (10) % , a ф % ф - г                      ^,( )

e гдеXr yYjJ^^cr    . ;Ar "

^A r '

^Хф ^ У ^jJ®Mct   .   ;^A ф

Аф

1 _;

7 ЮУ г ^с ’

1      (11)

= /                          ;

V ЮУ ф ^ о

Уравнения (15) подставим в (14):

H e ^{( r} ,ф ) = H e ^{( r} )

X _r , Х ф — постоянные распределения электромагнитной волны в материал кольца; A _r , A ф -эквивалентная глубина проникновения электро-

H e ( ф , r ) = H e ( ф )

chx_rr b ^ch X r ⁽ r B ⁺ 2)

сНХ ф ф

cos q 1 ф ;

b еНХф (arcsin—) 2 rB

cos p 2 r . ⁽¹⁶⁾

Л Р магнитного поля в материал; у = — —^ - фа-

С учетом того, что cos q 1 ф = cos p 2 r = 0 , т.е. ^q1 ^ф = ^p 2 ^r = ± 2^ , уравнение (10) принимает вид:

зовый угол между индуктированной ЭДС и вихревым током; Р - угол магнитных потерь.

Так как постоянные (11) являются комплексными величинами, то решение уравнения (10) ищется в комплексном виде через круговые и гиперболические функции:

TT TT f X ChXrr      TT / X

H С = H e ⁽ r )---A r _⁺ H e ⁽ ф )

ch X r ⁽ r e ⁺ 2)

Тогда уравнения (1) и

H С ⁽ r , ф ) = A i cos( q ^ + JP 1 г );

H e ⁽ ф , ^r ) = A 2 ^cos( Р 2 ^{r +} Jq 2ф ),

где A i , A 2 , P i , p 2 , q i ,q 2 - постоянные разложения (12).

H c ( r, ф ) = A i cos q 1 ф cos jp i r - A i sin q ^ sin jp i r ;

H e ( ф , r ) = A 2 cos p 2 r cos jq 2 ф - A 2 sin p 2 r sin jq 2 ф .

Определим вторые производные:

H e =

H e =

d ² H e ⁽ r , ф ) d r ²

d ² H C ( ф , r )

Э ф ²

= A i cos q 1 ф cos Jp i r ;

= A 2 cos p 2 r cos Jq 2 ф .

Сравнивая (13) с (11), запишем, что ^p i = ^X r = V ^yrJ^^ c ; ^q 2 = ^Х ф = ^ ф р^ Ст • Используя эти величины и связь с круговыми и гиперболическими функциями, получим:

<

H e ( r ф = A i ch x r r cos q 1 ф

H e ( ф , r ) = A 2 ^ch X ф Ф ^cos P 2 ^r

После подстановки граничных условий (6) и (7) в (14) получим выражения:

H e ^{( r} ) = A i ^ch X r ^{( r} e ⁺ 1) ,

, H c( r ) откуда A _i = --- c ' ь ;

^ch X r ^{( r} в ⁺ 2)

H e ⁽ ф ) = A 2 ^ch X ф (arcsin b- ) ^{2 r} B ’

H ф ) откуда A. =---- —c ^v '—-—

² , „ / ■ b ^ch X ф (^arcsin —)

^{2 r} B

.

- r

5-ф

^{Э H} С ^{( r}, ^ф ) _{=v F}

Э r       ^{Уф Е ф}

сК Х ф ф ch X ф (arcsin^b ) • ^{(17) 2 r} B

(2) принимают вид:

sh X r r ^{b sh} X r ( ^r B ⁺ 2)

^Э H С ^ф ) = y r E r     s^{h X} » » b ,₍₁8)

r           ^sh X ® (arcsin—)

2 r _B

где

E r = ^-PX r H С ^{( r}, ^ )th X r^a = ^- J to B_L c a Br ;

Е ф = -РХ ф Ис ( ф, r >Хф Ь = - j toB_L c b в_iф. ^{; (19)}

B С – комплекс действующего значения индукции, равномерно распределенный на эквивалентных глубинах a Br и Ь в ф , которые позволяют найти участки эквивалентного контура Lэ вихревых токов.

L э = a + b .              (20)

В эквивалентном контуре действует ЭДС

Э = 2( E r a + Е _ф Ь ) = - j-^ Ф .     (21)

Полученные выражения (17)-(20) позволяют определить сопротивления магнитных элементов НМАС силы вихревому и намагничивающему токам при действии на них силовой нагрузки.

Вихревые токи в эквивалентном контуре Lэ = a + b сечения кольца находятся путем интегрирования выражений (18):

I _rв

I фв

r

= с f ^- ф^dr =

cE_r     ch ф - 1

^{PX r} sh X ф (arcsin(- b -)) r _в

L

=cf—rdф=

^cEФ    ch ф - 1

^РХф sh X r ( r e + 2)

Сопротивления ЧЭ вихревым токам вычисляются с учетом выражений (19), (21) и (22) вычисляются:

Э a

Z e = , ^- =--- P e ^V

I _{r в}    сa_Er

= Э^

Zy , I ye

b JV -----p eJ * „ ^cbEy

Полное сопротивление вихревому току запишется как сумма выражений (23):

Zв = Z-e + Zye = —peV + -b-pe'^ , (24) caE-        cbEy где p - удельное электрическое сопротивление кольца; V-,Vy - углы сдвига между вихревым током и ЭДС по соответствующим направлениям эквивалентного контура; с – средняя длина пути магнитного потока;

где а в _- , Ь ву - эквивалентные глубины проникновения магнитного поля в ЧЭ НМАС; U_a - магнитная проницаемость кольца; ^a _- ^{, a} y - углы сдвига между намагничивающим током и магнитным потоком по соответствующим направлениям эквивалентного контура.

Эквивалентные глубины проникновения магнитного поля определяются с учетом выражений (11)

_ a ch 2 K 1 - cos2 K 2

^a B ^- - B ^y- K^h2 2 k ₁ + cos2 k ₂ ’ ⁽³⁰⁾

где K 1 , K 2 , K – определяются по соотношениям (26).

Углы сдвига между намагничивающим током и магнитным потоком

Kch 2 K + K sin 2 K₇ cos a _- = cos a y = — ²<    ^{1 1}      =;

K^sh 2 2 K ₁ + sin² 2 K ₂

, a chK - cos K ^aE- = b Ey =—.      ---^ ;

K\chK + cos K 2

Ksh 2 K + K ₇ sin 2 K₇ sin a _- = sin a y = —/ ^{1 2}     =

K^sh 2 2 K ₁ + sin² 2 K ₂

- эквивалентные глубины проникновения электрического поля в кольцо, определяются с учетом выражений (11):

K ^ = a V to - P o ; K = K cos(4 - y );

v v F ^     1           •   •(26)

K = K sinh - -); K - =- = Y - cos V- J Y - sW-

4 2

Углы сдвига между вихревым током и ЭДС:

Ki shK 1 + K ₂ sin K₂

cos Vr = cos Vy = —/ 1    22

K^sh ² K ₁ + sin ² K ₂

При отсутствии поверхностного эффекта, что имеет место при K = a-^toY-Pa — 0-5 ’ эквивалентные глубины проникновения электрического и магнитного полей равны bB- 2’aB-   2’bEy aE- 0-5aB- , а маг- нитная индукция распределяется равномерно по

Ba сечению элемента Bc =---и— . При этом можно

a пренебречь составляющими, пропорциональными круговым функциям в выражениях (27) и (31). Тогда

K shK + K sin K sin Vr = sin Vy = -- / 1     22

K^sh ² K ₁ + sin ² K ₂

K2• cosv = sin a = —2 = sin();

K 42

Сопротивление кольца намагничивающему току I ф = cH c по соответствующим направлениям эквивалентного контура определяются с учетом выражений (19) и (21)

„  ■ K л (32)

cos a = sin v = K- = cos("2 - V )-

Z r ф

Э r с H C

_ ato a B-   j_a,

^ a e c

С учетом всех принятых условий, сопротивление вихревому току, приведенное к виткам соответствующей обмотки, принимает вид

Z в

L_Э 0.5 a_Brc

P K П e ^{j V}

-<Рф

Э У с H C

^{b to b}By    ja

^ a e ^y .

c

Полное сопротивление намагничивающему току запишется как сумма выражений (28):

W где Kn =---- коэффициент приведения сопро-

^П W Ч

Z ф = ( a • a B- e^ja + b • Ь ву в^{]а у} ) ^ c ^ . (29)

тивления чувствительного элемента к соответствующей обмотке W; W ₄ = 1 - число витков ЧЭ.

Активная и индуктивная составляющие сопротивления вихревому току равны

г в = Z_B cos y ; х в = Z в sin y .    (34)

Полное сопротивление намагничивающему току, приведенное к виткам соответствующей обмотки, принимает вид toLэ aBr     2 ja

Z ф =         №< 7 K П e .     (35)

с

Активная и индуктивная составляющие сопротивления намагничивающему току:

Г ф = Z ф sin а ; Х ф = Z ф cos a . (36)

Приведенная к первичным виткам ЭДС эквивалентного контура

Э = го В С L_Э a_BrW 1 .         (37)

Поскольку сопротивления вихревому и намагничивающему токам расположены относительно друг друга параллельно, то комплекс полного результирующего сопротивления ЧЭ

Z в Z ф

Z D =           .

" P Z в + Z ф

Активная и реактивная составляющие rвrф         xвxф rp =--^; xp =---^.

r e ^{+ г}ф       ^хв ^{+ х}ф

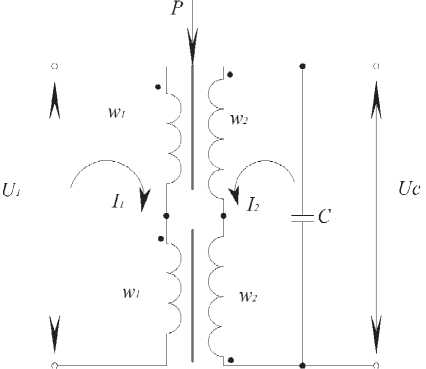
Рис. 3. Схема замещения магнитной цепи НМАС

При отсутствии поверхностного эффекта ( K <  0.5 ), что имеет место для ЧЭ МАПС из магнитомягкого феррита, глубины проникновения поля в элемент и его сопротивление вихревому току Z в практически не зависят от давления силы Р (механических напряжений а ), а сопротивление же намагничивающему току Z ф изменяется при действии силы Р (напряжений а ). При радиальном воздействии на кольцевой элемент выражение (35) приобретает вид [1, 2]:

, го8Э /

^Z ф = ( Д н с

^{05№ A} S ^a s A r o P ) К П_{ei a} (40)

л В ² a • b ²

Зависимости (33)-(40) позволяют определить электрические сопротивления чувствительных элементов НМАС и электрические потери и тангенс угла магнитных потерь tg P при силовом воздействии на них.

Схема замещения магнитной цепи НМАС представлена на рис. 3.

Для схемы замещения по второму закону Кирхгофа составляется систему алгебраических уравнений:

<

и _ч + U k = U 1

U ч - U k - U c = 0 .

где U Ч , U K , U C – соответствующие напряжения на обмотках ЧЭ и КЭ и контурном конденсаторе

Ск; U 1 - напряжение питания преобразователя.

Система уравнений (41) после перехода к магнитным индукциям принимает вид

f В ч + B k

<

В ч - B k

= В 1

^{- B} CK

= 0 .

где B Ч , B K – магнитные индукции в сердечниках ЧЭ и КЭ, B 1 – магнитная индукция в сердечниках элементов за счет напряжения питания U 1 ; B CK – магнитная индукция в сердечниках элементов за счет напряжения на конденсаторе.

Запишем выражения для магнитных индукций в виде

^ВЧ = ⁽ H 1 ⁺ H 2 ) ^Д Ч ^{; B}K = ⁽ H 1 ^- H 2 ) ^Д К ^;

B 1

U 1 H 2 c

; ^В CK               ;

^ S^ i         го ² SCk • w 2

где H 1 – напряженность магнитного поля, создаваемая в сердечниках ЧЭ и КЭ за счет протекания тока в первичной цепи преобразователя; H 2 – напряженность магнитного поля, создаваемая в сердечниках элементов за счет протекания тока во вторичной (измерительной) цепи; Д _ч и д_к - комплексные магнитные проницаемости ЧЭ и КЭ, получим

^Д _ч ^Д ч j ^4 ^tg P ч ; ^д _к = ^д к ^- j^Ktg ^ K ,

1д Р ч и tg ^ K — тангенсы магнитных потерь ЧЭ и КЭ, го - круговая частота питающего напряжения; S – сечение магнитопроводов; w 1 и w 2 - число витков обмоток возбуждения и измерительной, с – средняя длина пути магнитного потока в

элементе.

После подстановки (43) в систему уравнений (42) она преобразуется к виду

U ₁

^H 1⁽ Ц ⁺ Ц ) ⁺ H 2⁽ Ц ^- Ц ) - -c—; Ч K Ч ^kJV   to Sw

Cк 1        (45)

H 1^{( ц} _ч ^ _K) + ^H 2^{( ц} _ч + M _{K   2} 7 ) ^{- 0}

to cSw 2

В результате решения системы уравнений определим напряженность магнитного поля:

U 1 ( ц - ц > Cк ■ K T w_г H 2 ^- --------- ^K-----Ч -----------7---- T ^{. (}4⁶⁾

c ( Ц "  ^K ) "  4 ЦЦ^ cSw 2

где Ц _K "" Ц Ч -А Ц – изменение магнитной проницаемости [1], которое при радиальном воздействии силы Р на кольцо имеет вид:

.    0.563 Aas^»r₀P       w

Ац ------S s ,н 0—; KT - — - коэффи- kB 2 a ■ b 2               w 1

циент трансформации ЧЭ; w 1 - число витков обмотки возбуждения; f - частота питающего напряжения; S _- ab - сечение элемента; Ск - емкость контурного конденсатора, определяемая из условия резонанса токов при максимальной нагрузке P - P max на элемент [1],

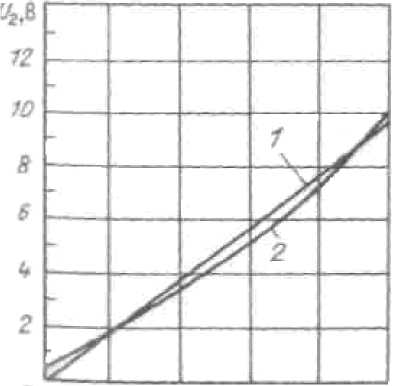
О 30   **Q Р,Н

Рис. 4. Выходная статическая характеристика: 1 – расчетная; 2 - экспериментальная т. к. Ck - const , то (2Zp -А2p)2 и (2xp - Ахp ) можно считать постоянными, т. к. ошибка при этом не превышает

2 х р — Ахр ск -                  X" , to(2Zp - АZp )2

А - ^{2 Х р А х р} ^ _W0% - 0.01% (2 Z_p - Z P _р )²

Предлагаемая методика использовалась для

А х p , А Z p - изменения индуктивного х р полного Z P сопротивлений ЧЭ при силовом воздействии на него, приведенные к той обмотке, в которой включен контурный конденсатор Ск.

При радиальном воздействии механической силы Р на кольцо напряжение поля H 2 принимает известный вид [1,2]

расчета устройств, кольцевые ЧЭ и КЭ которого имеют размеры 10х6х4,5 мм из феррита марки

2000НМ1 при радиальном воздействии силы от

0 до P max - 50 H , при напряжении и частоте питания U 1 - 4.5 B , f - 40 кГц .

Получены следующие результаты расчета: ц н - 4■Ю^-3 Гн / м при р - 0 Н ; Z в - 3.932 ^ 10 6 Ом ; Z ф - 650 Ом ; Z__p - 650 Ом ; U 2 - 9.85 В при

H 2 рад

^U i K T r o A s a s ц н fw 2 Cк ■ ^р 5.03 л Б ² ab ²( r о - 4 кц _н f ² cabw 2 )

,(48)

Р max

- 50 H .

На основании выражения (50) построена вы-

где U 1 – напряжение питающей сети; K T – коэффициент трансформации ЧЭ; r 0 – средний радиус кольца; A S - изотропная магнитострикция; ц н - начальная магнитная проницаемость; f -частота питающего напряжения; w 2 – число витков измерительной обмотки; Ск – емкость контурного конденсатора; Р – механическая сила; B – магнитная индукция; a , b – ширина и толщина кольца; c – длина четверти кольца.

Выходное действующее напряжение U 2 , снимаемое с конденсатора Ск , записывается выражением

ходная статическая характеристика U ₂ - f ( P ) , которая представлена на рис. 4. Сходимость дан-

ной характеристики относительно экспериментальной составляет не более 5%.

U 2

^- I 2

to C к

H 2 c 1 w 2 to C к

r ₀

0 H 2 , (49) fw Cк    ^,

которое после подстановки в него выражения (56) и (55) приобретает вид

U 2 рад

U 1 K_Tr 0 A s a s M _H ( 2 Z p - А Z p ) 2 P

5.03 К ² ab ² [ r )( 2 Z p -А Z p ) 2 - 2 ц н fabw 2 ( 2 x p -А х_p

^ ,(50)