Математическая модель вихря Тейлора

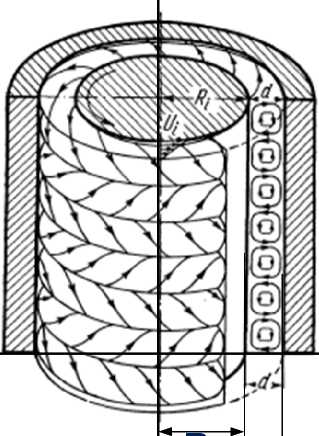
В [1] описывается классический эксперимент Тейлора – см. рис. 1, где показаны два цилиндры и вязкая жидкость в зазоре между ними. Внешний цилиндр с радиусом R 2 = R i + d неподвижен, а внутренний цилиндр с радиусом R 1 = R i вращается и тем самым создает основное течение U_i .

При некоторой скорости вращения в зазоре "между цилиндрами возникают правильно чередующиеся вихри с правым и левым вращением и с осями, параллельными направлению окружной скорости вращающегося цилиндра". Эти вихри катятся по окружности и не переходят с одной окружности на другую. В [1] описываются различные экспериментальные исследования такого течения, но его математическая модель отсутствует. Видимо, ее невозможно построить на основе известных уравнений гидродинамики. Ниже предлагается математическая модель такого течения, построенная в предположении, что, кроме известных массовых сил, в текущей жидкости возникают гравитомагнитные силы, существенно зависящие от скорости движения.

z

R 1

Рис. 1.

r

2.    Гравитомагнетизм

В [2] анализируются некоторые масштабные природные явления и неожиданные эксперименты. Доказывается, что они могут быть объяснены существованием гравитомагнетизма и значительных по величине сил гравитомагнитного взаимодействия -гравитомагнитных сил. Эти силы имеют значительную величину в вакууме.

В слабом гравитационном поле Земли можно пользоваться максвеллоподобными уравнениями для описания гравитомагнитных взаимодействий – максвеллоподобными уравнениями гравитомагнетизма (МПГ-уравнения). Взаимодействие между движущимися массами описывается гравитомагнитными силами Лоренца (далее ГЛ-силы), аналогичными силам Лоренца в электродинамике. Из аналогии между уравнениями Максвелла для электродинамики и МПГ следует, что существует также поток S гравитационной энергии.

Как уже отмечено, ГЛ-силы имеют значительную величину в вакууме. В потоке жидкости движущиеся молекулы разъединены вакуумом. Поэтому силы их гравитомагнитного взаимодействия могут быть значительными и влиять на характер течения.

Известно, что при увеличении скорости ламинарного течения жидкости или газа самопроизвольно (без наличия внешних сил) возникает турбулентное течение [3]. Механизм самопроизвольного перехода от ламинарного течения к турбулентному течению не найден. На основе этого в [4] обосновывается утверждение о первичности турбулентного движения.

На основе вышесказанного в [5] было предложено объяснение механизма возникновения турбулентных течений. Было показано, что движущиеся молекулы текущей жидкости взаимодействуют между собой аналогично движущимся электрическим зарядам. Силы такого взаимодействия могут быть рассчитаны и включены в уравнения Навье-Стокса как массовые силы. Уравнения Навье-Стокса, дополненные такими силами, становятся уравнениями гидродинамики для турбулентного течения. При этом для расчета турбулентных течений можно использовать известные методы решения уравнений Навье-Стокса.

Далее МПГ-уравнения используются для построения математической модели вихря Тейлора (аналогично тому, как они были использованы для построения математической модели трубку Ранка [6]).

3.    Математическая модель

В конструкции Тейлора существуют массовые токи. Обозначим их плотности как Jr., Jф, Jz. Эти массовые токи создают гравитомагнитные напряженности Hr, H ф, Hz. Плотности массовых токов и напряженности должны удовлетворять МПГ-уравнениям. Для стационарного случая, который имеет место в нашей задаче, эти уравнения (также, как и уравнения Максвелла для электродинамики) имеют вид div(H) = 0,(1)

rot(H) = J ,(2)

Кроме того, массовые токи должны удовлетворять условию непрерывности div( J) = 0

При моделировании будем использовать цилиндрические координаты r , ф , z - см. рис. 1. Тогда уравнения (1-3) примут вид:

H r  д H r  1 5 H   д H z +     + "     + r     д r   r д ф     d z		= 0 ,	(4)
1 д H z   а Н ф _ "я        я   = J r ’ r   д ф    д z			(5)
а H r -а нL = J д z      д r      ф ’			(6)
H Ф   9H Ф  1 д H r +           " r д r   r   д ф	- = J z	+ J o ,	(7)
J r   д З r   1 д J ф 11+ r д r   r д ф	8J^ = д z	: 0 .	(8)

Для сокращения записи в дальнейшем будем применять следующие обозначения:

co = cos(aф + xz),(9)

si = sin( аф + xz),(10)

где a, x — некоторые константы. В приложении 1 показано, что существует решение, имеющее следующий вид:

Jr . = jr (r co,(11)

3ф- = ф(r) si,

Jz . = jz (r) si ,(13)

Hr • = hr (r ^O ,(14)

Hr = hф( r)si,(15)

Hz • = hz (r)si ,(16)

где j(r), h(r) - некоторые функции координаты r. В приложении 1 показано, что указанное решение 5-ти уравнений (4-8) с 6-ю неизвестными функциями j(r), h(r) может быть найдено при данной функции jф (r) .

Функции j ^ ( r ) описывает массовые токи. В рассматриваемой конструкции эти токи возникают под действием из-за сил вязкости. Эти силы распределены по радиусу и это распределение зависит от того, какой из цилиндров вращается, увлекая вязким трением близлежащие слои воды. Очевидно, скорость вращения будет уменьшаться в сторону неподвижного цилиндра.

Мы не будем анализировать эти связи, а предположим, что в общем случае функция j _ф ( r ) имеет следующий вид:

j^X ^r ) = a + b ^r ,

где a , b - известные коэффициенты.

Пример 1.

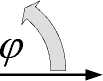
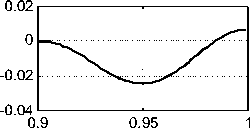
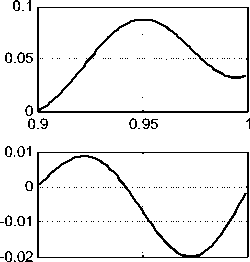
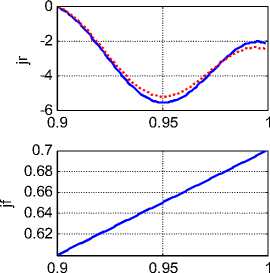
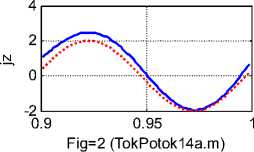
На рис. 2 (mode=4) показаны графики функций Jr (r), j/r), Jz (r), hr (r), h/r), hz (r) в зазоре конструкции. Эти функции вычисляются итеративно при данных а = 4, х = 63 , радиусе провода R1 = 0.9, R2 = 1 и функции j^(r) = -0.3 + r . В первой колонке показаны функции hr (r), h^(r), hz (r), а во второй колонке показаны функции jr (r), j^r), jz (r) . Вместе с функцией jz (r) пунктиром показана функция ja = 2sin( x),(18)

а вместе с jr (r) функцией пунктиром показана функция jn = (- 21 (1 - cos(Xr)) - 25 1(r - 0.9)).

Видно, что j_r ( r ) « j_rt ( r ) , j z ( r ) « j_zt ( r ) . Следовательно, существует такое решение уравнений (4-8), при котором

Jr (z) ~ jrt(r) cos(a^ + xz),(20)

Jz(r) « jzt(r)sin(aф + xz).(21)

• - см. также (9-12).

  
  
  
  
  
  
  
  
  
  
  
  

Пример 2.

На рис. 3 при условиях примера 1 показано поле токов J_r (r ) + J_z (r ) ) в вертикальном сечении зазора конструкции. Видны правильно чередующиеся вихри с правым и левым вращением. Это следует из (20, 21). Из рис. 3 следует, что массовые токи, т.е. струи жидкости совершают в зазоре круговые движения.

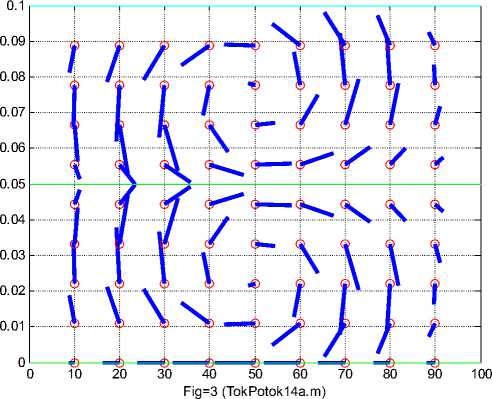
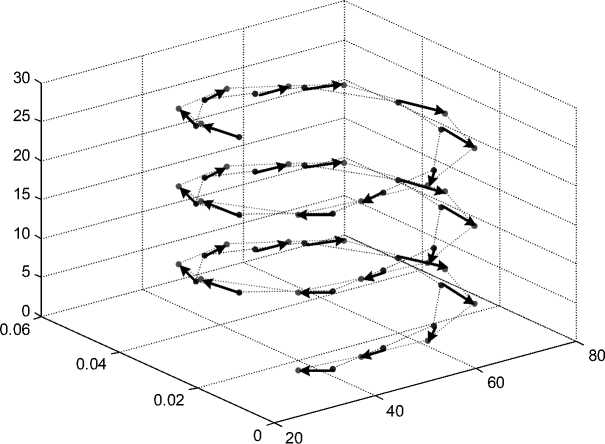
Рис. 4.

Пример 3.

Основное течение U_i превращает круговые движения жидкости в движение по спирали с осью – окружностью, проходящей по центральной линии кругового зазора. На рис. 4 показано векторное поле токов J_r ( r ) + J z ( r ) ) в отрезке такой спирали. Этот отрезок соответствует участку тороидальной спирали на рис. 1. Векторное поле показано только для одного радиуса этого тора. Синяя пунктирная линия изображает тор с этим радиусом, а красная пунктирная линия объединяет концы векторов ( J r ( r ) + J z ( r ) ) , исходящих из синей линии.

Характер рассмотренных движений соответствует движениям, наблюдаемым в экспериментах – см. рис. 1. Следовательно, можно утверждать, что вихри Тейлора объясняются гравитомагнетизмом. Влияние гравитомагнитных сил возрастает с увеличением скорости движения. Поэтому при малых скоростях наблюдается ламинарное течение, но с увеличением скорости существенную роль начинают играть гравитомагнитные силы. Появляется турбулентность. С дальнейшим увеличением скорости эти силы начинают превалировать и возникают упорядоченные вихри.

Приложение 1

Рассматривается решение уравнений (3.4-3.8) в виде функций (3.11-3.16). Далее производные по r будем обозначать штрихами.

Из (3.4) находим:

j (r )                      j (r )

• ——- co + j‘ (r) co + —— a • co + jz (r) x • co = 0

rr или j^r) + j’ (r) + j^r) a + jz (r) x = 0.(2)

rr

Из (3.5, 3.6, 3.7) находим:

h2^) + hr(r)+ ^^( ) a + %• hz(r) = 0,(3)

rr

• 1    • hz(r)a - h^(r)X = jr (r )

r

• - hr(r)x - hZ(r) = j^(r).

Из (3.8) находим:

h (r )             1

• —   + h , ⁽ r ) + • h r ^{( r a} = J_z ^{( r} ) .                        (6)

rr

Итак, получено 5 уравнений (2-6) с 6-ю неизвестными функциями j(r), h(r) . Поэтому одну из функций можно определить произвольно. Мы определим функцию j,(r). В этом случае алгоритм решения этих уравнений имеет следующий вид:

• 1.    Устанавливаем начальные (при r = 0 ) нулевые значения всех перечисленных функций, кроме j , ( r ) .

• 2.    Определяем функцию j , ( r ) .

• 3.    Из (2) находим:

• 3.    Из (3) находим:

j ( r ) ^j , ^{( r} )

jr(r) = -     —-—a - jz(r)X = 0.

rr jr = Ud + jr"dr •(8)

• hr = -hr? - "—a - hzX,

hr = "rod + hr" dr.(10)

• 5    Из (5) находим:

• hZ(r) = - j,( r)- hr(r )z.(11)

• hz = hzold + h’z" dr .

• 6.    Из (4) находим:

• h,( r) = (hz ( r )a / r — h (r )У X.

• h- (r) = (hz (r )a / r - j'r (r ))/ X.

• 7.    Из (6) находим:

h. _(r)1

• jz(r) = h,(r)+ —   + • hr(r ^-(15)

• 8.    Переходим к п. 2 с новым значением переменной r .

rr