Математическая модель вязкопластичной смазки подшипников скольжения с деформируемой опорной поверхностью

Введение. Как известно, применяемые в настоящее время жидкие смазочные материалы (масла) состоят из масляной основы (базового масла) и композиции присадок, придающих маслам необходимый уровень функциональных свойств [1, 2]. Добавки полимеров с высоким молекулярным весом придают маслам вязкопластичные свойства. Работа подшипников, работающих на вязкопластичных смазках, достаточно изучена [3—6]. Анализ этих работ показывает, что в выполненных исследованиях опорная поверхность подшипников считается абсолютно жёсткой.

В области подшипников с жидкостной плёнкой смазки появилось новое направление подшипников с нежёсткой опорной поверхностью. Жёсткость такой поверхности имеет такой же или даже меньший порядок величины по сравнению с жёсткостью плёнки смазки. Подшипники с нежёсткой поверхностью имеют явные преимущества по сравнению с подшипниками жёсткой опорной поверхностью. Эти преимущества — допустимость больших несоосностей и деформации рабочей поверхности, а также терпимость к присутствию посторонних частиц между рабочими поверхностями. Кроме того, податливость эластомера под действием давления смазки приводит к появлению своего рода губы, ограничивающей утечку сдавливающей смазки из подшипника.

Таким образом, в условиях уменьшенного смазкой питания подшипник с нежёсткой поверхностью может сохранить гидродинамическую или гидростатическую плёнку смазки. В этом отношении он значительно превосходит подшипник с жёсткой опорной поверхностью. Целью данного исследования является оценка рабочих характеристик такого подшипника и, в последующем, сравнение их с хорошо известными характеристиками подшипника такого же типа, но имеющего жёсткую опорную поверхность.

Постановка задачи. Рассматривается установившееся движение вязкопластичной смазки в зазоре радиального подшипника с податливой опорной поверхностью. Шип вращается с угловой скоростью со, а подшипник неподвижен. В полярной системе координат (г, 0) с полюсом в центре шипа уравнения шипа и деформированного контура опорной поверхности запишутся в виде г' = г0, г' = rY + ecos0 + аф(0).

Здесь г₀ — радиус шипа; а — радиус подшипника; е — эксцентриситет; аф(0) — функция, характеризующая деформацию опорной поверхности подшипника.

При оценке влияния деформации опорной поверхности подшипника на его основные рабочие характеристики ограничимся максимальным значением функции аф(0). Введём обозначения ар(е) = а<р*; при 9 е [о, 2л] ар* = тахар(э).

Основные уравнения и граничные условия. Будем исходить из безразмерных уравнений движения вязкопластичной смазки для случая «тонкого слоя» и уравнения неразрывности, которые получаются из уравнений Генки-Ильюшина методом оценок

d2U dp . ди ди п

—г = т^- + А — + -л- = 0 dr² de dr 50

Система уравнений (1) решается при следующих граничных условиях

(/=0, и = 0 при Г = 1+Г|СО50

и = -1, и = 0 при г = 0; р(0) = Р(2п) = -^-

е х                         х                                                       , рсог2

Здесь п = $; б = г, + аф - г₀ ; и,, = шби, и_е = шг_ои — компоненты вектора скорости; р' = ^₂° р —

, х . 2тпб2 _              „                _ гидродинамическое давление, г' = гп+ог; А =—У—--безразмерный параметр, обуславливаю-ЦСОГр щий вязкопластичные свойства смазки; рД — давление питания; т0 — предельное напряжение сдвига.

К уравнению (1) необходимо добавить безразмерную систему уравнений Ламэ для «тонкого слоя»

^^ = 0, ^- = 0. dr*2 5г*2

Здесь в области занятой упругим слоем размерные величины и'_г, и^ связаны с безразмерными соотношениями

u'_r, =U*U_r,, Ug =U*Ug, Г' = r_x +6/*, б_т =r₂ -r_lz

где и* — характерная величина компонента вектора перемещений; r₂-ri — толщина упругого слоя.

В переменных (г, 6) и (г*, 6) уравнение недеформированного контура, прилегающего к смазочному слою, можно записать в виде

■^- + П cos 0 = ^(0), г* = ri! cos 0 = Л₂ (0), П = |-, Ф =у-

Уравнение деформированного контура и внешнего контура упругого слоя прилегающего к жёсткой поверхности подшипника соответственно запишется в виде

г = 1 + П cos 0 = Л₃ (0), г* =1+ П1 cos0 = Л₄(0).

Система уравнений (3) решается при следующих граничных условиях

N—§-dr*

Эи "dr

.. 9иг,

, М—^г- r=h_v^ ^Г

^' ^Уе1г-=Л₄(6)    ^uAr=h ₂(В) О'

где

_N G,W6. „ G^l + a^u'^ мсогцб/ (1-а)ро)г₀²б₁ '

Gr — модуль сдвига; о — постоянная Мусхелишвили; р = max р, 9 е [0, 2п]; р — безразмерное гидродинамическое давление в смазочном слое радиального подшипника с жёсткой опорной поверхностью.

Граничные условия (7) означают равенство касательных и нормальных направлений на недеформированной упругой поверхности подшипника, прилегающей к смазочному слою.

Интегрируя первое уравнение смазки (3) с учётом граничных условий (7), будем иметь

Г М М ’

Воспользуемся приближённой формулой

Ir-^fe)1

С учётом формул (5) и (6) получим

аф* Р б ~ М

Из уравнения (9) с точностью до членов

для аф* получим следующее приближённое

уравнение

ЭД ~~j^\r^ r*r

(Ю)

Из формулы (10), как и ожидалось, следует, что отношение максимального значения деформации к радиальному зазору прямо пропорционально безразмерному максимальному давлению и обратно пропорционально упругогидродинамическому параметру М. При М -ж аф* -> 0.

Точное автомодельное решение задачи (1)—(2) будем искать в виде

« = ”Ч^),о = -^+1/(г,е),Ф = Ф(у,« = ^

v = »®h-(eV^,^A = ^^-HD

Подставляя (11) в (1) и (2) придём к следующей системе обыкновенных дифференциальных уравнений и граничных условий к ним

Ф” = с2, u" = cv У-^и' = 0(12)

Ф'(0) = 0; Ф'(0) = 0, 17(0) = -1, и(1) = 0, 5(0) = 0, б(1) = 0; j(7(^ = 0.(13)

о

Решение задачи (12)—(13) легко находится непосредственным интегрированием. В результате будем иметь

Ф' = ^р-У, ОД^у-^-ф-!,(14)

где q = -б, константа с2 в дальнейшем определяется из условия /:(0)=/:(2п).

Гидродинамическое давление с учётом (14) определяется из последнего уравнения системы (11). С точностью до членов С(п³) для определения Р приходим к уравнению

^■ + Д = -6^1-2ncos6 + |n2 +^cos29j + c2(l-3ncos0 + 3n2 +3q2cos26)(15)

Из условия периодичности гидродинамического давления в принятом нами приближении для константы с2 получим следующее выражение с2 =Д + 6-ЗДп2-9п2(16)

Интегрируя (15) с учётом (16) будем иметь р = —бп sin 6 — 3/4г| sin 6 + 9п2 sin 26 + — q2 sin 26 + —(17)

'                                           2

где р = р(6) при 6 = 6_1Z где 61 является корнем уравнения

-бпсозб! -ЗЛпсозб! +18n2cos261 н-ЗД^соэгб! =0, п = е/(г1 -г0).(18)

Перейдём к определению безразмерной несущей способности и безразмерной силы трения. С учётом формул (14) и (17) для Ry — безразмерной составляющей несущей способности и без размерной силы трения получим следующие выражения

R 2п

R„ =—— = — f Р sin 6сУ6 = 6пп + ЗДг|п о

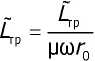
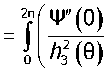
yVO))                 Ч

+ —об = 2п + 4г|²п - Дп + - Дпг|²

^(б)/          1        2 1

Численный анализ аналитический выражений (19) с учётом (17) и (18) проводился при следую'

щих значениях параметров

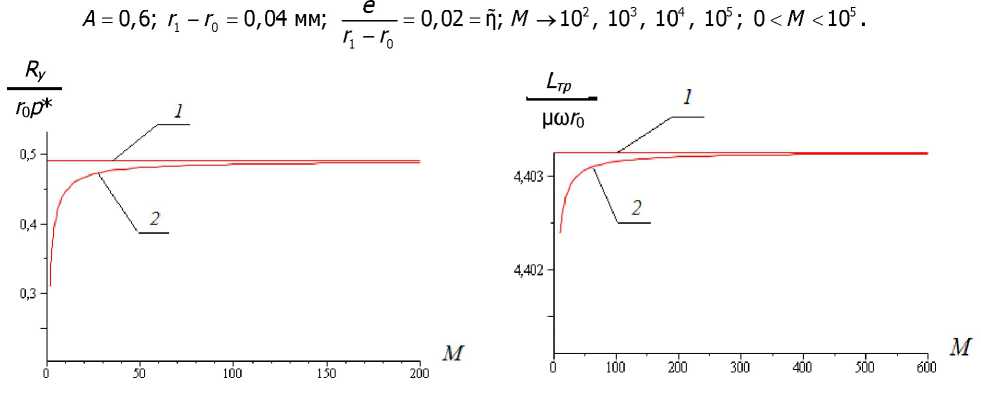
Рис. 1. Зависимость безразмерной несущей способности от Рис. 2. Зависимость безразмерной силы трения от параметра параметра М: 1 — Эф* = 0, А = 0,6; 2 — Эф* * 0, А = 0,6             М: 1 — Эф* = 0, А = 0,6; 2 — Эф* * 0, А = 0,6

Выводы. Из полученных выражений (19) и зависимостей, приведённых на рис. 1 и 2, следует, что:

• 1.    Значение несущей способности и силы трения подшипника с податливой опорной поверхностью меньше, чем у такого же подшипника с жёсткой опорной поверхностью.

• 2.    С увеличением значения упругогидродинамического параметра М, значение несущей способности и силы трения подшипника возрастает. При М -»<» несущая способность подшипника и сила трения стремятся к соответствующему значению для случая подшипника с жёсткой опорной поверхностью.

• 3.    В принятом в работе приближении значение несущей способности и силы трения прямо пропорционально параметру пластичности А.