Математическая модель влияния озонотерапии и плазмафереза на электролитный баланс, у больных токсическим зобом

inv^r1^11J

Dnunuun

иеггдл tlll/l

ОЗОНОТЕРАПИИ И ПЛАЗМАФЕРЕЗА НА ЭЛЕКТРОЛИТНЫЙ БАЛАНСУ БОЛЬНЫХ ТОКСИЧЕСКИМ ЗОБОМ

М. Д. Романов, доктор медицинских наук, А. В. Водянова

Нами был проведен полный двухфакторный эксперимент по изучению эффективности озо-нотерапии и плазмафереза при лечении больных тиреотоксикозом. В качестве критерия оптимизации был назначен уровень ионов фосфора, кальция, магния, железа. Выбор критерия оптимизации обусловлен, с одной стороны, требованиями математического аппарата, а с другой — тем фактом, что повышенное число сердечных сокращений, высокое артериальное давление, тремор пальцев рук, раздражитель ность и утомляемость связаны с нарушением электролитного баланса Ж4 — Na4» и «Са4 — Р4» (вообще, кардиальный синдром и психоэмоциональные нарушения являются самыми частыми проявлениями снижения уровня циркулирующего К4). Одновременно гипокалиемия, гипокальциемия считаются основными причинами проксимальной миоплегии при тиреотоксикозе. И хотя патогенез гипокалиемии не вполне понятен, можно предположить, что возникает дефицит К4- №4-привкой АТФ-азы, в

ВЕСТНИК Мордовского университета | 2006 | № 2

результате чего нарушается трансмембранный транспорт соответствующих ионов.

Целью нашего исследования является получение математической модели, описывающей экспериментальные данные полиномом той или иной степени. На первой стадии исследования мы рассматривали линейную модель, Выбор плана эксперимента связан с определением числа экспериментальных точек и такого их расположения в факторном пространстве, которое позволило при минимальном числе опытов получить необходимую информацию. При выборе плана мы составили матрицу планирования, где указали условия проведения всех опытов, образующих выбранный план эксперимента. Каждый фактор варьировали на двух уровнях. Следует иметь в виду, что одной из важных особенностей исследований, построенных на теории полного факторного эксперимента (ПФЭ), является повышенная требовательность к точности измерения при фиксировании факторов.

Таблица

Включение сеансов плазмафереза (фактор хЛ, озонотерапии (фактор х2) и стандартной медикаментозной терапии в проводимых исследованиях (фактор х0)

№ исследования	хо
1	+	+	+
2	+	-	+
3	+	+
4	+		-

В результате исследования было найдено 32 значения критерия оптимизации, каждый из которых имел 2 повторения. Случайные ошибки измерений описываются нормальным распределением и поэтому характеризуются двумя величинами — выборочной дисперсией s² и выборочным средним х,

^(^-х)²     У^х.

$2= —------- х = —--’ и-1         и а доверительный интервал измерений определяется из соотношения:

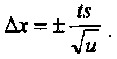
где t — критерий Стьюдента (табличная величина для назначенной доверительной вероятности а и фактическом числе измерений и).

При подозрении, что «выпадающий» результат измерений соответствует «промаху», расчетную величину t-критерия сравнивают с табличной:

У — X

В случае несправедливости этого неравенства результат измерения считается недостоверным и отбрасывается.

В нашем случае промахов было 2, а наибольшая дисперсия составила 0,0576 при доверительном интервале ±0,30.

Выявление ошибок наблюдений связано с учетом числа повторений этих наблюдений п, а так как априори принят нормальный закон распределения результатов отдельных опытов, то при обработке эксперимента в целом определяли среднее арифметическое значение критерия оптимизации в отдельном опыте и дисперсию ошибки опыта:

sL = —--------- V. = —---’ n-1      "" n где з2ош — дисперсия ошибки опыта; п — число наблюдений (повторений опыта); у.ц — значение критерия оптимизации для отдельного наблюдения; уа — среднее арифметическое значение критерия для отдельного опыта.

У(ут-у.У

^=-----:---= 0,0576’ л-1

У Ут у„ =---- =30,96.

Переход от ошибок опытов к ошибке эксперимента в целом связан с усреднением дисперсий ошибок, а это возможно только в случае однородности дисперсий. Проверяют однородность дисперсий с помощью критерия Кох-рена:

G = 2™»_

Только в случае однородности дисперсий ошибок отдельных опытов имеет смысл определять дисперсию ошибок эксперимента; в целом — дисперсию воспроизводимости:

Ьп.

=0,652, где N — число опытов, S? — дисперсия ошибки для t-того опыта, Д — число степеней свободы для t-того опыта.

По результатам ПФЭ были найдены значения коэффициентов уравнения регрессии для следующих микроэлементов:

для фосфора:

у = 0,99 +1 .013jc, + 1.08х₂ + 1.11XjX₂, для кальция:

у = 2.53 + 2.52х₁ + 0.77х₂+ 2.64х,х₂ , для магния:

у = 0,76 + 0,7?Х) + 2,3х2 + 0,77Х]Х2, для железа:

у - 18,17 + 23,23х, + 12,53х2 +21,77х,х2 , где хр х2, х3 — кодированные значения факторов, у — значение критерия оптимизации.

х = £lz£io £ где с. и сш — натуральные значения фактора на двух уровнях, 8 — натуральное значение интервала варьирования фактора.

Линейные коэффициенты регрессии были рассчитаны по формуле:

N

^«. У.

к - 1________ где х.ц — значение фактора в «-ом опыте, уц — значение критерия оптимизации в этом же опыте, N — число опытов в матрице планирования эксперимента.

После расчета коэффициентов уравнения регрессии необходимо оценить значимость каждого коэффициента и определить адекватность аппроксимирующего полинома. Коэффициент уравнения считается значимым, если его величина Д6 больше доверительного интервала при назначенной доверительной вероятности:

A2>,=±-^L где sf/ — ошибка воспроизводимости, a t — критерий Стьюдента.

В нашем случае наименьшая дисперсия воспроизводимости s2 = 0,652. С учетом этого найдены с 95 % доверительной вероятностью границы доверительных интервалов для рассматриваемых коэффициентов регрессии:

Ai,, .A₌2.13^07

Гипотезу об адекватности регрессионной модели проверяют с помощью критерия Фишера:

.у2

F =_^_<р

5И где ?2 --------------— дисперсия адек-

" jv-x-fc-O ватности модели, X — число коэффициентов аппроксимирующего полинома, пд — число повторений (наблюдений) нулевого опыта. В случае справедливости приведенного неравенства считается, что модель адекватно описывает процесс и может быть использована для поиска оптимума.

Расчетное значение критерия Фишера составило 2,01 при табличной величине 2,35.

Таким образом, нами была получена линейная математическая модель, описывающая влияние сеансов озонотерапии и плазмафереза на динамику состояния больных тиреотоксикозом. Необходимо проведение дальнейших исследований для оптимизации курса терапии в зависимости от состояния пациентов.

Поступила 20.11.06.

ВЕСТНИК Мордовского университета | 2006 | № 2