Математическая модель встраиваемого оптоволоконного TFBGs-датчика с наклонными брэгговскими решетками для диагностирования сложного деформированного состояния в полимерных композитных конструкциях

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2025PNRPU MECHANICS BULLETIN

© Паньков Андрей Анатольевич - д. ф.-м. н., доцент, профессор кафедры механики композиционных материалов и конструкций, e-mail: ,

Оптоволоконные датчики, в частности, со встроенными в световод брэгговскими решетками, широко используются в различных отраслях науки и техники [1– 5] для измерения различных физико-механических величин, что необходимо для современных систем управления и адаптации свойств ответственных конструкций, например, аэрокосмической техники к меняющимся условиям эксплуатации. Оптоволоконные датчики могут быть установлены на поверхности конструкции или внедрены внутрь, например, полимерной композитной конструкции на этапе ее производства с целью «самодиагностики», т.е. индикации наличия возможных технологических дефектов типа пор, непроклеев, смятий армирующих волокон или слоев ткани (препрега), удаленного мониторинга эволюции изменения свойств композита на структурном уровне [6; 7], диагностирования типа и величины напряженного состояния, локации опасных зон с критическими нагрузками, выявления возможных эксплуатационных микроповреждений, в частности: разрывов армирующих элементов, отслоений по межфазным поверхностям и растрескивания матрицы (связующего) полимерного композита, актуальной оценки прочности композита и конструкции в целом [8–18]. Современные технологии сенсорной тех- ники позволяют создавать оптоволоконные брэгговские решетки различной структуры и назначения [19–21]. Необходимость разработки новых встраиваемых оптоволоконных датчиков для диагностирования сложного напряженно-деформированного состояния внутри полимерных композитных конструкций обусловлена потребностью повышения точности, чувствительности, ширины рабочего диапазона измерений и упрощения технологии создания таких датчиков. Предложенные в [22] оптоволоконные TFBGs-датчики с наклонными брэгговскими решетками (Tilted Fiber Bragg Gratings) предназначены для диагностирования сложного напряженно-деформированного состояния внутренних и/или приповерхностных областей – окрестностей TFBGs-датчиков, встроенных внутрь или установленных на поверхности диагностируемых полимерных композитных конструкций. Оптоволоконные TFBGs-датчики имеют вид многожильного кабеля, в котором шесть однонаправленных световодов со встроенными различно наклоненными брэгговскими решетками размещены с фиксированным взаимным, например гексагональным, расположением в протяженном цилиндрическом сплошном полимерном корпусе датчика. Известные оптоволоконные датчики [23–27] с наклонными брэгговскими решетками не использовались ранее для диагностирования сложного напряженно-деформированно- го состояния внутри нагруженных полимерных композитных конструкций. Рассматриваемые оптоволоконные TFBGs-датчики с наклонными брэгговскими решетками более просты в изготовлении по сравнению, например, с известными встраиваемыми оптоволоконными пьезоэлектролюминесцентными [28; 29] и механофотолюми-несцентными [30] датчиками сложного напряженного состояния с учетом, что современные технологии изготовления различных оптоволоконных брэгговских решеток хорошо отработаны и имеют высокий уровень развития. Необходимость использования в TFBGs-датчиках световодов с наклонными брэгговскими решетками обусловлена однонаправленностью световодов в датчике, например, по оси r3, из-за чего их продольные деформации г33(k, равны значению компоненты е33 диагностируемого тензора £* макродеформаций. Поэтому при использовании традиционных «поперечных» брэгговских решеток это равенство е33(k, = е33 обусловливает одинаковые деформационные изменения значений периодов брэгговских решеток и, как результат, одинаковые значения информативных смещений измеряемых спектров отражений для различных световодов как функций лишь компоненты е33 без учета других компонент е* диагностируемого тензора £*, k = 1,6. Таким образом, невозможность использования однонаправленных световодов с традиционными брэгговскими решетками для прогнозирования сложного деформированного состояния £* обусловливает применение в TFBGs-датчиках световодов с наклонными брэгговскими решетками, в которых отражающие элементы (области периодического изменения коэффициента преломления) ориентированы под некоторыми заданными углами к поперечным сечениям световодов и, как результат, на информативные значения деформированных периодов которых теперь уже будут влиять все искомые компоненты е* диагностируемого тензора макродеформаций £* .

Цель исследования - разработка математических моделей и нахождение численных значений характеристик - управляющих и информационных передаточных коэффициентов встраиваемых оптоволоконных TFBGs-датчиков [22] для диагностирования сложного напряженно-деформированного состояния внутри нагруженных полимерных композитных конструкций с использованием световодов с различно наклоненными брэгговскими решетками.

Принцип диагностированя

Принцип «шести направлений» диагностирования сложного деформированного состояния £* (как суперпозиции трех растяжений и трех сдвигов в декартовой системе координат x, y, z) с использованием предло- женного TFBGs-датчика проиллюстрируем на примере, в котором упругие свойства световодов и в целом датчика не отличаются от упругих свойств однородной области конструкционного материала. Искомые шесть независимых компонент е* тензора деформаций £* можно найти по измеренным (каким-либо возможным способом) значениям продольных деформаций ek вдоль шести различных некомпланарных направлений lk для этой области из решения системы шести линейных алгебраических уравнений ej(k)il(k,j = ek в виде a, x = e, kp p k относительно искомых величин x = {е11, e22, e33,2e23,2е13,2е12 } , где индексы k, p = 1,6, передаточные коэффициенты ak 1 = l(k)1l(k)1 ’ ak2 = l(k)2l(k)2 ’ ak3 = l(k)3l(k)3 ’ ak4 = l(k)2l(k)3 ’ ak5 = l(k)1l(k)3 ’ ak6 = l(k)1l(k)2

для рассматриваемого случая однородности (т.е. независимости от координат) упругих свойств области «ма-териал/встроенный датчик», так как имеем равенство a _kp = l ( _k ) i l ( _k ) j , в котором численные значения пары индексов ij связаны с численным значением индекса p следующим образом: 11 ^ 1, 22 ^ 2, 33 ^ 3, 23 ^ 4, 13 ^ 5, 12 ^ 6. Возможность нахождения искомых компонент е j тензора деформаций £* по совокупности значений продольных деформаций e k подтверждена вычислением численного значения главного определителя Л = | a_kp | / 0 для заданных модельных значений координат l _{( k} ) i направлений l _k . Значения продольных деформаций e k гипотетически возможно измерить с использованием, например, шести разнонаправленных световодов с однотипными «поперечными» брэгговскими решетками, проходящими через диагностируемую область по различным направлениям l _k , где k = 1,6, что трудно реализуемо на практике, особенно при множестве локальных областей - «макроточек» диагностирования.

В предложенном оптоволоконном TFBGs-датчике [22] значения продольных деформаций e_k по шести различным некомпланарным направлениям l k измеряются с использованием шести однонаправленных световодов с различно наклоненными брэгговскими решетками с нормалями n _k = l _k к своим отражающим поверхностям. Однонаправленность световодов позволяет их компактно и монолитно объединить общим гибким полимерным (например, цилиндрическим) корпусом (рис.1) с функцией буферного слоя - механического фильтра для «защиты» измерительных элементов (брэгговских решеток) от случайных быстро осциллирующих составляющих £‘ ( r ) - пульсаций микроуровневых деформаций композитной области в окрестности встроенного

TFBGs-датчика. В результате из внешней области через буферный слой на измерительные элементы TFBGs-датчика транслируется лишь величина постоянной макроскопической составляющей £* действительного неоднородного поля деформаций £(r)=£*+£‘(r) композитной области в окрестности встроенного датчика; трансляцию характеризуют значения передаточных коэффициентов akp датчика. Учет неоднородности расчетной области «композит/встроенный датчик» по упругим свойствам отразится на уточнении решения для передаточных коэффициентов akp TFBGs-датчика, численные значения которых akp ≠ l(k)il(k) j будут учитывать особенности укладки однонаправленных, например, по оси z, световодов в поперечной плоскости xy, в частности, правильную гексагональную укладку или в ряд по оси x [22], и могут быть найдены в результате численного моделирования системы «композит/встроенный датчик» для совокупности шести простых случаев макродеформаций ε1*1, ε*22, ε*33 , 2ε*23, 2ε1*3, 2ε1*2 при «единичных» значениях. В общем взаимное расположение однонаправленных световодов в TFBGs-датчике осуществляется из принципа технологичности сборки и компактности их укладки, чтобы поперечный размер (диаметр) TFBGs-датчика с буферным слоем не превышал установленный характерный размер квазиоднородности диагностируемого поля макродеформаций в исследуемой области композитной конструкции. Отметим, что результатом диагностирования являются компоненты е* тензора деформаций £* в декартовой локальной системе координат x, y, z, к которой «привязаны», т.е. в которой были найдены информативные передаточные коэффициенты akp TFBGs-датчика. На технологическом этапе встраивания оптоволоконного TFBGs-датчика в структуру полимерного композиционного материала возможны случайные повороты локальной системы координат x, y, z TFBGs-датчика вокруг продольной оси z=r3 относительно лабораторной системы координат r1,2,3 конструкции, что необходимо учи*

тывать при переходе от найденных компонент ε _ij в локальной системе x, y, z к соответствующим значениям компонент в лабораторной системе координат r 1,2 , 3 . Повороты TFBGs-датчика в поперечной плоскости xy несущественны лишь при вычислении и использовании инвариантов тензора деформаций £* и/или напряжений σ _ij = C _ijmn ε _mn , не зависящих от поворотов системы координат, где C i*mn - компоненты тензора C * эффективных упругих свойств композита в осях x, y, z локальной системы координат. Избежать таких поворотов можно, используя TFBGs-датчик ленточной формы с прямоугольным поперечным сечением и плотной укладкой световодов в ряд по ширине узкой тонкой полимерной ленты – корпуса датчика [22]. В результате встроенный внутрь полимерной композитной конструкции, находящейся при эксплуатационных нагрузках, оптоволоконный TFBGs-датчик позволяет определить искомый тензор макродеформаций ε ^* сложного деформированного состояния в своей композитной окрестности по результатам измерений спектров отражения всех шести световодов.

Математические модели TFBGs-датчиков

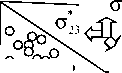
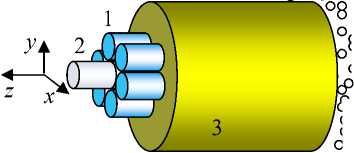
Встраиваемые оптоволоконные TFBGs-датчики диагностирования        сложного        напряженно- деформированного состояния области (в окрестности датчика) нагруженных полимерных композитных конструкций изображены на рис. 1, в которых шесть световодов с различно наклоненными брэгговскими решетками расположены, например, вокруг вспомогательного световода с традиционной «поперечной» брэгговской решеткой (см. рис. 1, а) или пьезоэлектрического кабеля с выходами электродов для подключения управляющего электрического напряжения Ucon (см. рис. 1, b).

° о%0

о о 8

о ° о о

\ о о

* ^σ 21

8О°

О о о

а                                                   b

Рис. 1. Встраиваемые оптоволоконные датчики: 1 – световоды с наклонными ВБР; 2 – световод с традиционной ВБР ( а ); 3 – буферный слой (корпус); 4 – диагностируемая область; 5 – пьезоэлектрический кабель с выходами электродов ( b )

Fig. 1. Built-in fiber optic sensors: 1 – light guides with tilted FBG; 2 – light guide with traditional FBG ( a ); 3 – buffer layer (housing); 4 – diagnosed area; 5 – piezoelectric cable with electrode outputs ( b )

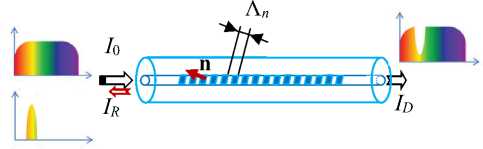
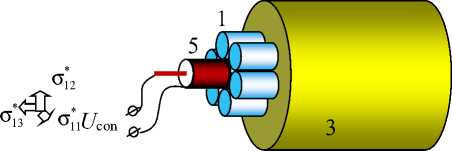
Рис. 2. Наклонная ВБР с периодом Λ n по нормали n к отражающим поверхностям

Fig. 2. Tilted FBG with period Λ n along normal n of reflecting surfaces

Волоконная брэгговская решетка представляет собой оптический интерферометр, встроенный в световод (рис. 2), в рассматриваемом случае для k -й «наклонной» брэгговской решетки – это периодическое изменение показателя преломления k -го световода с начальным (т.е. до деформации) периодом Λ n 0( k ) по нормали n k к отражающим поверхностям, например, одномодового оптического волокна, где k = 1,6 . Векторы n k – нормали отражающих поверхностей –являются некомпланарными, например, с координатами (рис. 3)

n _{( k ) x} = cos α _k sin θ _k , n _{( k ) y} = sin α _k sin θ _k , n _{( k ) z} = cos θ _k , (1) выраженными через ориентационные углы α, θ сферической системы координат:

αk =(k-1)π/3, θk =θmin+(k-1)(θmax-θmin)/5, (2) выполняются равенства θ1=θmin, θ6= θmax с учетом k = 1,6 , θmin , θmax – заданные минимальное и максимальное значения угла θ, например: θmin = π/4, θmax =π/3. Угол между продольной осью z и отражающими поверхностями брэгговской решетки k-го световода равен π/2-θk. Полимерный цилиндрический корпус TFBGs-датчика (см. рис. 1) обеспечивает несколько функций: фиксацию заданного взаимного расположения, например, гексагональной укладки световодов, защиту световодов от внешних механических повреждений. При этом корпус как буферный слой между измерительными элементами – брэгговскими решетками и диагностируемой микронеоднородной композитной областью в окрестности встроенного в конструкцию (нагруженной эксплуатационными термосиловыми воздействиями) TFBGs-датчика – выполняет еще важную функцию механического фильтра для защиты измерительных элементов от негативных стохастических быстро осциллирующих составляющих деформационных полей из композитной окрестности. В результате работы такого фильтра имеем детерминированную функциональную зависимость результатов измерений от диагностируемых макроскопических значений напряжений σ* и/или деформаций ε* композитной окрестности, что обусловливает постоянство переда- точных информационных коэффициентов a(k)mn встраиваемого TFBGs-датчика. Таким образом, оптимальный диаметр корпуса как буферного слоя должен, во-первых, минимизировать «паразитные» влияния пульсаций σ’, ε’ – стохастических отклонений (деформационных полей σ, ε от соответствующих усредненных значений σ*, ε*) быстро осциллирующих составляющих, обусловленных вероятностным расположением структурных неоднородностей композита вблизи внешней цилиндрической поверхности корпуса TFBGs-датчика, внедренного в полимерную композитную конструкцию, и, во-вторых, не превышать характерный размер «квазиоднородности», т.е. существенного изменения полей макродеформирования σ*, ε*, превышение которого приводит к необходимости учитывать градиенты ∇σ* , ∇ε* этих полей при расшифровке измеренных спектров отражений световодов. Из первого условия следует, что толщина полимерной прослойки (между световодами и внешней цилиндрической поверхностью корпуса) должна составлять не менее двух значений характерного размера неоднородностей, например, диаметра армирующих волокон в композитной окрестности TFBGs-датчика. Второе условие обусловлено тем, что передаточные информационные коэффициенты a(k)mn встраиваемого TFBGs-датчика определяются для макрооднородного напряженно-деформированного состояния без учета градиентов ∇σ* , ∇ε* в представительной области dV* «композит/встроенный датчик». Наличие в датчике (см. рис. 1, b) пьезоэлектрического кабеля [31; 32] позволяет управлять характеристиками оптоволоконных брэгговских решеток, т.е. изменять период решеток посредством деформирования световодов в результате обратного пьезоэлектрического эффекта кабеля при подключении к выходам его электродов управляющего электрического напряжения Ucon. Для световодов датчика считаем известными начальные спектры отражения R0(k) (λ) их брэгговских решеток с центральными длинами волн λ0(k) =2neff(k)Λn0(k) [23], где neff(k) = neff /cosθk – эффективный показатель преломления k-го световода для центральной длины волны λ0(k) , θk – угол между вектором нормали nk и продольной осью z этого световода (рис. 3), neff – для традиционной брэгговской решетки [33; 34].

При сложном деформировании ε* композитной окрестности датчика (см. рис. 1) и случая действия на выходы электродов пьезоэлектрического кабеля управляющего электрического напряжения U con в световодах датчика (см. рис. 1, b ) возникают деформации

ε ( k ) ij ⁼ n U ( k ) ij^U con ^{+ N} ( k ) ij αβ ε αβ ^{,                 (3)}

и, как следствие, имеем осевые деформации en(k) = ε(k)αβn(k)αn(k)β                        (4)

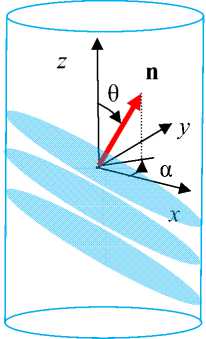
Рис. 3. Ориентационные углы α, θ нормали n поверхностей отражения наклонной брэгговской решетки

Fig. 3. Orientation angles α, θ of normal n for reflection surfaces of the inclined Bragg grating по нормали nk к отражающим поверхностям k-й брэгговской решетки, где n(k)i – координаты нормали nk, ε(k)ij – компоненты тензора εk деформаций световода; тензоры управляющих коэффициентов влияния nU(k)ij=ε(k)ijε*=0/Ucon находим при условиях: Ucon ≠ 0 , ε* = 0. В выражении (3) компоненты N(k)ijmn тензора Nk концентраций деформаций введены равенством

ε ( k ) ijU _con = 0 ^{= N} ( k ) ij αβ ε ^* αβ ^{; (5)}

здесь и далее тензорные немые индексы суммирования обозначены греческими, а свободные индексы – латинскими буквами со значениями 1,3. При численном моделировании компоненты ε _{( k ) ij} тензора ε k деформаций отождествляем с осредненными по области V k k -го световода значениями, т.е е k = j V е dV / V k , где s ( r ) - действительное поле деформаций (найденное из решения краевой задачи теории упругости для системы «компо-зит/встроенный датчик») как функция координат r ∈ V _k .

В результате из выражений (3), (4) следует формула для осевых деформаций

*

e n ( k ) ⁼ a U ( k ) ^U con ⁺ a ( k ) αβ ε αβ ^,

по нормали n k световодов, где a _{U ( k )} , a _{( k ) mn} – управляющие скалярные и информационные тензорные передаточные коэффициенты TFBGs-датчика (см. рис. 1, b )

a U ( k ) ⁼ n ( k ) α n ( k ) β n U ( k ) αβ ^, a ( k ) mn ⁼ n ( k ) α n ( k ) β ^N ( k ) αβ mn ^{.    (7)}

Величины осевых деформаций (6) могут быть записаны en(k)=aU(k)Ucon+a(k)αβσαβ                 (8)

через искомые компоненты σ ^* _mn тензора σ ^* макронапряжений композитной окрестности встроенного TFBGs-датчика, где a ₍ ⁽ _k ^σ ₎ ⁾ _mn – информационные передаточные коэффициенты TFBGs-датчика (см. рис. 1, b ), выполняется равенство a _{( k ) mn} = a ₍ ⁽ _k ^σ ₎ ⁾ _αβ C _α ^* _{β mn} или a _{( k ) mn} = C _m ^* _{n αβ} a ₍ ⁽ _k ^σ ₎ ⁾ _αβ с учетом симметрии C _i ^* _jmn = C _m ^* _nij тензора C ^* эффективных упругих свойств композита [35; 36].

Наличие осевых деформаций e _{n ( k )} (6) брэгговских решеток световодов обусловливают измеряемые информативные «смещения» по оси абсцисс

^Δ n ( k ) ^≡λ ε ( k )⁽ ε ^{) -λ} 0( k ) ^=λ 0( k ) e n ( k )             ⁽⁹⁾

спектров отражения

R ε ( k ) ≡ R 0( k ) ( λ-Δ n ( k ) ),                (10)

где λ= 2 n Λ – центральные длины волн спек- ε ( k )          eff( k ) n ( k )

тров отражения R _{ε ( k )} деформированных брэгговских решеток с учетом величин деформированных периодов Λ _{n ( k )} ( ε ) = Λ _{n 0( k )} (1 + e _{n ( k )} ). Из равенств (6), (8), (9) следует система шести линейных алгебраических уравнений

a(k)αβεαβ = Δn(k) / λ0(k)-aU(k)Ucon в виде

**

^a (1)11 ^ε 11 ^{+ a} (1)22 ^ε 22 ^{+ ... + a} (1)12 ^ε 12 ^{= b} (1)

...(11)

***

a(6)11ε11 + a(6)22ε22 +... + a(6)12ε12 = b(6) , где коэффициенты правой части

b(k) = Δn(k) / λ0(k)-aU(k)Ucon для нахождения искомых шести независимых компонент ε1*1 , ε*22 , ε*33 , ε*23 , ε1*3 , ε1*2 тензора макродеформаций ε* или компонент σ1*1 , σ*22 , σ*33 , σ*23 , σ1*3 , σ1*2 тен*

зора макронапряжений σ

( σ )      *

a ( k ) αβ σ αβ ⁼ ( k )

по измеряемым значениям смещений Δ _{n ( k )} спектров отражения R _{ε ( k )} (10) световодов при заданном управляющем электрическом напряжении U con. (12). Формулы (3), (6), (8), (11), (12) получены для оптоволоконного датчика на рис. 1, b , с наличием пьезоэлектрического кабеля и действием управляющего электрического напряжения U con .

Формулы для оптоволоконного TFBGs-датчика на рис. 1, а, без пьезоэлектрического кабеля имеем, полагая Ucon=0; например, система алгебраических уравнений (11), (12) примет вид a'(k)αβ εαβ =Δn(k)/λ0(k),                  (13)

где информационные передаточные коэффициенты датчика на рис.1, а a'(k)mn= n(k)αn(k)βN'(k)αβmn,                 (14)

в общем отличные от аналогичных коэффициентов a _{( k ) mn} TFBGs-датчика на рис. 1, b , где N ' _{( k ) ijmn} – компоненты тензора N ' _k концентраций деформаций с учетом разложений осредненных по области каждого k -го световода деформаций

ε ^'( k ) ij ^{= N '}( k ) ij αβ ε αβ                         ⁽¹⁵⁾

и осевых деформаций вдоль некомпланарных векторов nk для TFBGs-датчика (см. рис. 1, а) по аналогии (4), (5).

Передаточные коэффициенты: a _{U ( k )} , a _{( k ) mn} , a ₍ ⁽ _k ^σ ₎ ⁾ _mn и a ' _{( k ) mn} , a ' ⁽ ₍ ^σ _{k )} ⁾ _mn –- характеристики соответствующих оптоволоконных TFBGs-датчиков на рис.1, b , а , могут быть определены в результате численного моделирования методами механики композитов или экспериментально с использованием образца композитного материала со встроенным оптоволоконным датчиком (см. рис. 1).

Результаты численного моделирования

Рассмотрим вычисление информационных передаточных коэффициентов a'(k)mn оптоволоконного TFBGs-датчика на рис. 1, а, с учетом заданных ориентаций отражающих e'n(k)= ε'(k)αβn(k)αn(k)β                      (16)

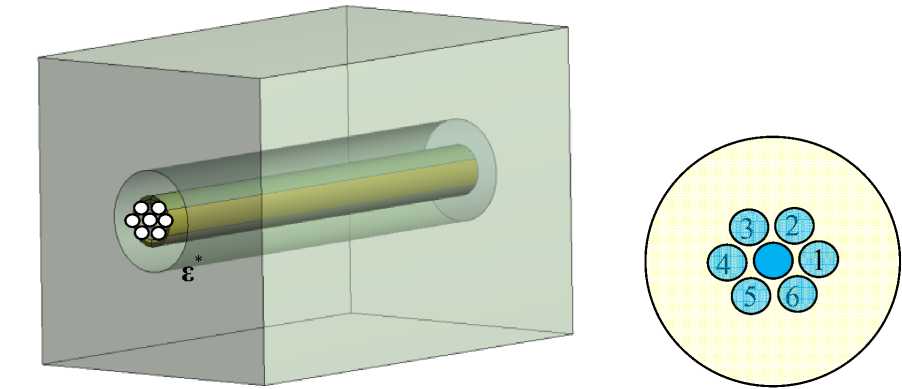
Рис. 4. Расчетная схема ( а ), расположение и нумерация световодов в буферном слое ( b ) датчика

Fig. 4. Design diagram ( a ), location and numbering of optical fibers in the buffer layer ( b ) of the sensor

b

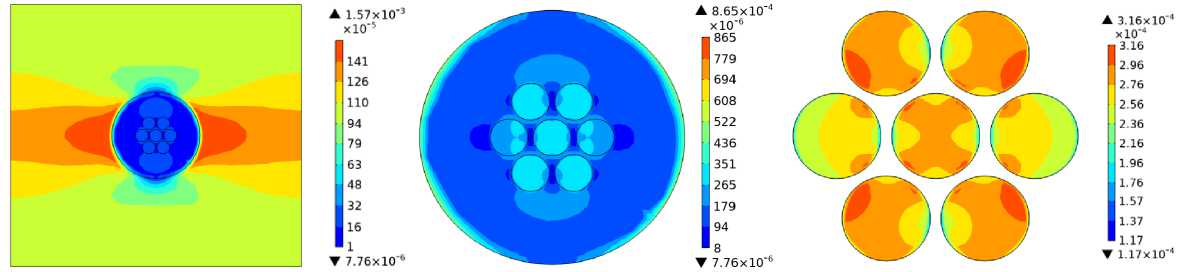
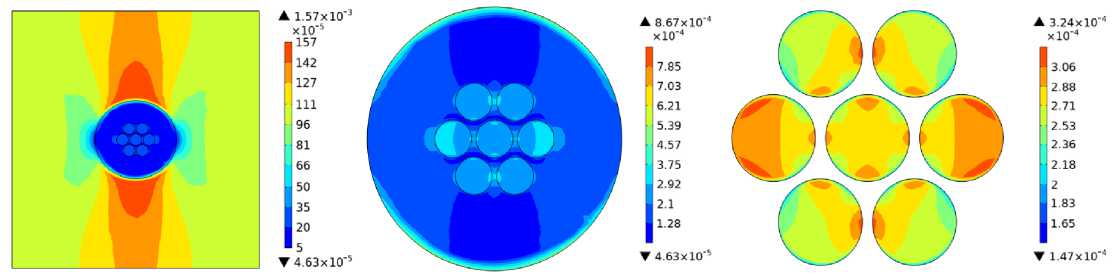
Рис. 5. Поля осевых ε ₁₁ при ε ₁ ^* ₁ = 0,001 ( а ), ε ₂₂ , ε ^* ₂₂ = 0,001 ( b ), ε ₃₃ , ε ^* ₃₃ = 0,001 ( c ) и сдвиговых ε ₂₃ при ε ^* ₂₃ = ε ^* ₃₂ = 0,001 ( d ), ε ₁₃ ,

ε ₁ ^* ₃ = ε ^* ₃₁ = 0,001 ( e ), ε ₁₂ , ε ₁ ^* ₂ = ε ^* ₂₁ = 0,001 ( f ) деформаций по серединному поперечному сечению расчетной области

Fig. 5. Fields of axial ε ₁₁ at ε ₁ ^* ₁ = 0.001 ( a ), ε ₂₂ , ε ^* ₂₂ = 0.001 ( b ), ε ₃₃ , ε ^* ₃₃ = 0.001 ( c ) and shear ε ₂₃ at ε ^* ₂₃ = ε ^* ₃₂ = 0.001 ( d ), ε ₁₃ , ε ₁ ^* ₃ = ε ^* ₃₁ = 0.001 ( e ), ε ₁₂ , ε ₁ ^* ₂ = ε ^* ₂₁ = 0.001 ( f ) strains along the middle cross-section of the design area

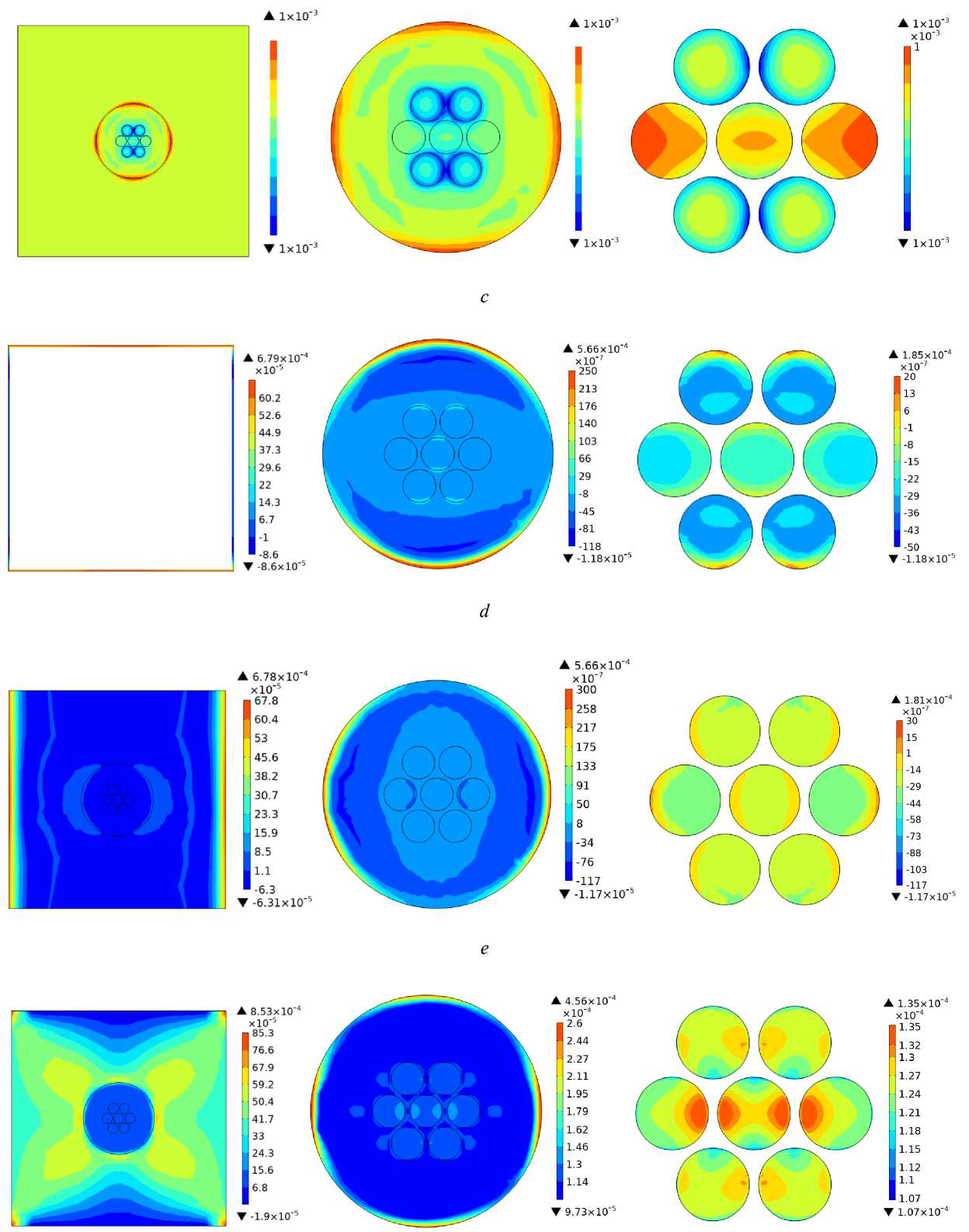
f

Рис. 5. Окончание

Fig. 5. The end

Таблица 1

Относительные величины ε / ε ^* при ε ^* ≠ 0

(k)ij 1111

Table 1

Relative value of ε _{( k ) ij} / ε ₁ ^* ₁ if ε ₁ ^* ₁ ≠ 0

Номер волокна, k	ε ( k )11 / ε 11	ε ( k )22 / ε 11	ε ( k )33 / ε 11	ε ( k )23 / ε 11	ε ( k )13 / ε 11	ε ( k )12 / ε 11
0	0,2781	-0,1037	0	0	0	0
1	0,2617	-0,1002	0	0	0	0
2	0,2839	-0,1018	0	0	0	-0,0130
3	0,2839	-0,1018	0	0	0	0,0129
4	0,2617	-0,1002	0	0	0	0
5	0,2839	-0,1051	0	0	0	-0,0129
6	0,2839	-0,1051	0	0	0	0,0129

Таблица 2

Относительные величины ε/ ε* при ε* ≠0 (k)ij     2222

Table 2

Relative value of ε _{( k ) ij} / ε ^* ₂₂ if ε ^* ₂₂ ≠ 0

Номер волокна, k	ε ( k )11 / ε 22	ε ( k )22 / ε 22	ε ( k )33 / ε 22	ε ( k )23 / ε 22	ε ( k )13 / ε 22	ε ( k )12 / ε 22
0	0,0075	0,2781	0	0	0	0
1	-0,0059	0,2921	0	0	0	0
2	0,0150	0,2687	0	0	0	-0,0122
3	0,0151	0,2687	0	0	0	0,0122
4	-0,0058	0,2921	0	0	0	0
5	0,0150	0,2687	0	0	0	-0,0122
6	0,0150	0,2687	0	0	0	0,0122

Таблица 3

Относительные величины ε _{( k ) ij} / ε ^* ₃₃ при ε ^* ₃₃ ≠ 0

Table 3

Relative value of ε _{( k ) ij} / ε ^* ₃₃ if ε ^* ₃₃ ≠ 0

Номер волокна, k	ε ( k )11 / ε 33	ε ( k )22 / ε 33	ε ( k )33 / ε 33	ε ( k )23 / ε 33	ε ( k )13 / ε 33	ε ( k )12 / ε 33
0	-0,2240	-0,2240	1	0	0	0
1	-0,2519	-0,1980	1	0	0	0
2	-0,2116	-0,2384	1	0	0	-0,0235
3	-0,2115	-0,2385	1	0	0	0,0233
4	-0,2518	-0,1981	1	0	0	0
5	-0,2115	-0,2384	1	0	0	-0,0234
6	-0,2115	-0,2384	1	0	0	0,0234

Таблица 4

гл™.™/***

Относительные величины ε _{( k ) ij} / ε ₂₃ при ε ₂₃ =ε ₃₂ ≠ 0

Relative value of ε / ε ^* if ε ^* =ε ^* ≠ 0 ( k ) ij     23         23       32

Table 4

Номер волокна, k	ε ( k )11 / ε 23	ε ( k )22 / ε 23	ε ( k )33 / ε 23	ε ( k )23 / ε 23	ε ( k )13 / ε 23	ε ( k )12 / ε 23
0	0	0	0	0,1207	0	0
1	0	0	0	0,1225	0	0
2	0	0	0	0,1200	0	0
3	0	0	0	0,1200	0	0
4	0	0	0	0,1225	0	0
5	0	0	0	0,1200	0	0
6	0	0	0	0,1200	0	0

Таблица 5

Относительные величины ε / ε ^* при ε ^* =ε ^* ≠ 0 ( k ) ij 13             13       31

Table 5

Relative values of ε _{( k ) ij} / ε ₁ ^* ₃ if ε ₁ ^* ₃ = ε ^* ₃₁ ≠ 0

Номер волокна, k	ε ( k )11 / ε 13	ε ( k )22 / ε 13	ε ( k )33 / ε 13	ε ( k )23 / ε 13	ε ( k )13 / ε 13	ε ( k )12 / ε 13
0	0	0	0	0	0,1207	0
1	0	0	0	0	0,1192	0
2	0	0	0	0	0,1216	0
3	0	0	0	0	0,1216	0
4	0	0	0	0	0,1192	0
5	0	0	0	0	0,1216	0
6	0	0	0	0	0,1216	0

Таблица 6

Относительные величины ε / ε ^* при ε ^* =ε ^* ≠ 0 ( k ) ij 12             12       21

Table 6

Relative values of ε _{( k ) ij} / ε ₁ ^* ₂ if ε ₁ ^* ₂ = ε ^* ₂₁ ≠ 0

Номер волокна, k	ε ( k )11 / ε 12	ε ( k )22 / ε 12	ε ( k )33 / ε 12	ε ( k )23 / ε 12	ε ( k )13 / ε 12	ε ( k )12 / ε 12
0	0	0	0	0	0	0,1277
1	0	0	0	0	0	0,1264
2	0	0	0	0	0	0,1257
3	0	0	0	0	0	0,1257
4	0	0	0	0	0	0,1264
5	0	0	0	0	0	0,1257
6	0	0	0	0	0	0,1257

Таблица 7

Информация о передаточных коэффициентах a ' _{( k ) mn} TFBGs-датчика

Table 7

Information gear ratios a ' _{( k ) mn} TFBGs-sensor

Номер волокна, k a (k)11 a (k)22 a (k)33 a (k)23 a (k)13 a (k)12 0 0 0 1 0 0 0 1 0,131 -0,003 0,374 0 0,122 0 2 -0,009 0,108 0,309 0,103 0,06 0,06 3 -0,01 0,118 0,244 0,102 -0,059 -0,066 4 0,171 -0,004 0,181 0 -0,116 0 5 -0,013 0,137 0,119 -0,095 -0,056 0,077 6 -0,014 0,146 0,061 -0,09 0,053 -0,082 поверхностей наклонных брэгговских решеток световодов (1), (2). Численные значения деформаций ε(k)ij (табл. 1–6) световодов и искомых информационных передаточных коэффициентов a'(k)mn (табл. 7) оптоволоконного датчика (рис. 1, а) с учетом равенств:

^a ( k )23 ^{= a} ( k )32 ^{, a} ( k )13 ^{= a} ( k )31^{, a} ( k )12 ^{= a} ( k )21

находим из рассмотрения расчетной области «компо-зит/встроенный датчик» (рис. 4) при шести простых случаях, в частности, трех осевых: ε1*1 , ε*22 , ε*33 и трех сдвиговых: γ*23 = 2ε*23 , γ1*3 = 2ε1*3 , γ1*2 = 2ε1*2 деформиро- ваний ε* расчетной области в виде параллелепипеда.

В табл. 1–7 случай k=0 соответствует центральному световоду датчика (см. рис. 1, а, рис.4) с традиционной поперечной решеткой, т.е. ненаклонной брэгговской. TFBGs-датчик в виде составной цилиндрической области «буферный слой/световоды» с радиусом световодов 0,4 мм, межцентренным расстоянием между световодами с гексагональной укладкой 0,9 мм, радиусом цилиндрического буферного слоя 2,8 мм расположен в центральной области параллелепипеда с ребрами: l1=l2=16,8 мм, l3=27,2 мм, ориентированными вдоль соответствующих поперечных r1,2, и продольной r3 координатных осей. Отметим, что на поля деформирования световодов и, как результат, численные значения передаточных коэффициентов оптоволоконного TFBGs-датчика влияют не абсолютные, а относительные размеры структурных элементов расчетной области «композит/встроенный датчик». Выполняются условия идеального контакта – непрерывность векторов перемещений и напряжений на межфазных поверхностях. Изотропные упругие свойства световода были заданы через модуль Юнга E(1) = = 50 ГПа и коэффициент Пуассона ν(1) =0,25, для полимерного корпуса E(2) = 0,73 ГПа, ν(2) =0,46. Трансверсально-изотропные с осью симметрии r3 упругие свойства параллелепипеда (стеклопластик) задавались через эффективные характеристики, в частности: поперечный и продольный модули Юнга: E1* = 10,017 ГПа, E3* = 31,217 ГПа, коэффициенты Пуассона: ν1*2 = 0,521, ν1*3 = 0,304, модули сдвига в поперечной G1*2 = 3,294 ГПа и продольной G1*3 = 3,581 ГПа плоскостях. Эти эффективные характеристики получены в обобщенном сингулярном приближении [35; 36] для трансверсальноизотропных упругих свойств однонаправленного волокнистого стеклопластика с объемной долей 0,6 ориентированных по оси r3 волокон, когда модули Юнга и коэффициенты Пуассона изотропных упругих свойств эпоксидной матрицы 3 ГПа, 0,4 и стекловолокон 50 ГПа, 0,25 соответственно. Отметим, что в общем для анизотропных, в частности волокнистых, композитов эффективные коэффициенты Пуассона могут принимать численные значения < 0 или > 0,5 [36; 37].

Численное моделирование – расчет распределений деформационных полей (рис. 5; табл. 1–6) для расчетной представительной области «композит/встроенный датчик» (см. рис. 4, а ) и нахождение численных значений (см. табл. 7) информационных передаточных коэффициентов a ' _{( k ) mn} оптоволоконного датчика (см. рис. 1, а ) осуществлено для различных случаев нагружений представительной области (см. рис. 4, а ) с использованием многопроцессорного вычислительного комплекса Центра высокопроизводительных вычислительных систем Пермского национального исследовательского политехнического университета в программной системе конечно-элементного анализа ANSYS. Расчетная область (см. рис. 4, а ) была дискретизирована на 18 ⋅ 10⁶ конечных элементов, из которых 12 ⋅ 10⁶ – для области самого датчика с корпусом. Для решения систем линейный алгебраических уравнений использован итерационный решатель метода сопряженных градиентов JacobiConjugateGradient (JCG) solver, который позволил существенно сократить время счета в сравнении с решателем Sparsedirectequationsolver (SPARSE); время счета для базового варианта задачи составило около

10 ч для SPARSE и 6 ч для JCG. Осуществлена проверка сходимости результатов расчета, выявлено, что в пределах менее 1 % стабильность искомых численных значений достигается при числе N > 55 000 элементов дискретизации расчетной области.

Заключение

Разработаны математические модели встраиваемых оптоволоконных TFBGs-датчиков (см. рис. 1) с различно наклоненными брэгговскими решетками (см. рис. 2) для диагностирования сложного напряженно-деформированного состояния внутри полимерных композитных конструкций (см. рис. 1, а ); различные пространственные ориентации отражающих поверхностей для различных световодов были заданы (1), (2) через координаты некомпланарных нормалей n k к этим поверхностям. Численное моделирование функционирования оптоволоконного TFBGs-датчика (см. рис. 1, а ) осуществлено для расчетной области «композит/встроенный датчик» (см. рис. 4, а ) в рамках линейной теории упругости. Представлены (см. рис. 5) цветовые эпюры распределений различных компонент ε _ij поля деформаций ε ( r ) по серединному поперечному сечению расчетной области (см. рис. 4, а ) при соответствующих простых случаях ее макродеформирования ε ^* _ij , при этом численные значения осредненных по области каждого k -го световода компонент деформаций ε ' _{( k ) ij} представлены в табл. 1–6. Далее значения компонент деформаций ε ' _{( k ) ij} (см. табл. 1–6; рис. 4) использованы для вычисления (16) осевых деформаций e ' _{n ( k )} вдоль некомпланарных векторов n k и в результате найдены численные значения искомых (14) информационных передаточных коэффициентов a ' _{( k ) mn} (см. табл. 7) оптоволоконного TFBGs-датчика на рис. 1, а , с учетом заданных (1), (2) ориентаций отражающих поверхностей наклонных брэгговских решеток световодов датчика. Таким образом, задача диагностирования сложного напряженно-деформированного состояния σ *, ε * элементарного макрообъема d V * (см. рис. 1, а , рис. 4) внутри нагруженной термосиловыми воздействиями композитной конструкции в локальной окрестности встроенного в нее оптоволоконного TFBGs-датчика сводится к решению системы линейных алгебраических уравнений, например, (11), (12), относительно искомых шести независимых компонент: ε ₁ ^* ₁ , ε ^* ₂₂ , …, ε ₁₂ тензора макродеформаций ε с использованием TFBGs-датчика с наличием (см. рис. 1, b ) или (13) без (см. рис. 1, а ) управляющего пьезоэлектрического кабеля по значениям информативных смещений Δ _{( k )} измеряемых спектров отражения R _{ε ( k )} световодов.