Математическая модель зеркально-симметричного накладного измерительного конденсатора
Автор: Джежора Александр Александрович
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Приборные иследования и разработки для разных областей
Статья в выпуске: 4 т.21, 2011 года.
Бесплатный доступ
Представлены результаты расчета основных параметров зеркально-симметричного накладного измерительного конденсатора. Для численного 2D-моделирования были использованы методы интегральных уравнений и зеркальных отображений. Поверхность каждого электрода рассматривалась в виде двух параллельных ламелей. Такой подход упростил процедуру численного решения двухмерной задачи по сравнению с применением стандартных конечно-элементных схем. Он позволяет выполнять расчет электрических полей плоских слоистых сред с меньшими затратами. Программа численных расчетов реализована в MAPLE.
Зеркально-симметричный накладной измерительный конденсатор, модель, анизотропия, точность
Короткий адрес: https://sciup.org/14264747
IDR: 14264747 | УДК: 621.317.39.084.2
Текст научной статьи Математическая модель зеркально-симметричного накладного измерительного конденсатора
Целый ряд материалов обладает ортогональной анизотропией физико-механических свойств и относится к ортотропным средам. Самой большой чувствительностью к анизотропии диэлектрических свойств обладает зеркально-симметричный накладной измерительный конденсатор (ЗСНИК) [1] в виде пары ленточных многосекционных на- кладных измерительных конденсаторов (МНИК), известных как FEF sensors. Поля МНИК направлены встречно. Сечение секции преобразователя ЗСНИК показано на рис. 1.
Модель, представленная в статье, учитывает толщину электродов и подложек. В статье приведены экспериментальные данные для подтверждения работоспособности разработанной модели.
Рис. 1. Сечение секции ЗСНИК.
1 — высокопотенциальные электроды; 2 — низкопотенциальные электроды; 3, 4 — экраны
МОДЕЛИРОВАНИЕ ЗСНИК
Цель данной работы — построить математическую модель многосекционного зеркально-симметричного накладного измерительного конденсатора, рассчитать основные характеристики ЗСНИК исходя из геометрических размеров контролируемого материала и самого чувствительного элемента с учетом диэлектрических свойств материала и диэлектрических свойств чувствительного элемента.
Для численного 2D-моделирования был использован метод интегральных уравнений Фредгольма первого рода совместно с методом зеркальных отображений. В отличие от метода конечных элементов данный метод менее требователен к вычислительным ресурсам и позволяет проводить расчеты емкостных датчиков без потери точности за более короткий промежуток времени.
Расчеты проводятся на примере одной секции многосекционного ЗСНИК (рис. 1). Электрическое поле, создаваемое высокопотенциальными электродами 1, проникая через контролируемый материал, замыкается на низкопотенциальные электроды 2. Поле ограничено в пространстве подложек экранами 3 и 4. Низкопотенцильные электроды 2 имеют потенциал земли V 2 . Область контроля определяется геометрическими размерами секции датчика: шириной секции r , межэлектродным расстоянием h и толщиной электродов d .
Основная идея заключалась в том, что при создании математической модели ЗСНИК каждый электрод рассматривался в виде двух бесконечно тонких электродов, разнесенных в пространстве на расстояние, равное толщине d реальных электродов (рис. 1). Такое рассмотрение электродов не противоречит физике, в силу того что поверхности электродов эквипотенциальны и поле внутри электродов отсутствует. Поле выходит за пределы внутренней области и имитирует поле ЭП, в том числе и в воздушных карманах, образованных реальными электродами.
Метод интегральных уравнений
В качестве исходного выражения при составлении интегральных уравнений для потенциалов точек поверхности электродов использовалось выражение логарифмического потенциала:
V = -^ln —о, (1) 2πεε0 rMN где σ — заряд на отрезке l в сечении электрода, rMN — расстояние между рассматриваемой точкой М и переменной точкой N (зарядом, создающим поле в точке M).
Для записи интегральных уравнений поверхностная плотность зарядов на электродах обозначалась двумя индексами σ l k . Первый индекс соответствует номеру электрода на рис.1, а второй — стороне поверхности: 1 — соответствует поверхностной плотности заряда на стороне электрода, обращенной к контролируемому материалу; 2 — на стороне электрода, обращенной к подложке. Очевидно, в силу симметрии
о k ( x ) = о k ( - x ) ; о 2 k ( x ) = о 2 k ( - x ) ; (2)
о 3 ( x ) = о 3 ( - x ) = о 4 ( x ) = о 4 ( - x ).
Аналогичные выражения можно записать для электродов 1 и 2 верхнего накладного измерительного конденсатора.
Промежутки интегрирования разбивались на участки, где искомые функции поверхностной плотности заряда σ ( x ) принимали постоянные значения. Это позволило в дальнейшем, согласно методу Крылова—Боголюбова, выносить их за знаки интегралов, преобразуя систему интегральных уравнений в систему линейных алгебраических уравнений (СЛАУ). Границы интегрирования записывались в следующем виде.
Для участков на поверхности электродов, обращенной к контролируемому материалу:
о 1 - q i „ 1 - q i 1
в = r -----, a = r ---— для 1 = 1,2,3, ^ , n ;
i 0 1- qn , i 0 1 - qn,
1 - q - n 1 - q - n
Pi = r-(r-r1) 2n2 , a= r-(r-r1) 2n2(
1 q2
для i = n 1 + 1, „., n 1 + n 2 .
Для участков на поверхности электродов, обращенной к подложке:
P i = r o
1 - q 3 - n 1
— I
n 2
1 - q П 4
, a i = r o
1 - q 3 - n 1
-I
n 2
1 - q П 3
для i = n1 + n 2 + 1,..., n1 + n 2 + n 3;
1 - q - n 1 - n 2 - n 3 - 1
p = r - ( r - r 1 )----1 4 - q n 4---- , (4)
a i = r - ( r - r)
1 - q 4 - n 1
— I
n 2
-i
n 3
1 - q 44
для i = n 1 + n 2 + n 3 + 1,..., n 1 + n 2 + n 3 + n 4 .
На экране:
P i = r
1 - q 5 - n 1
- n 2 - n 3 - n 4
1 - q 5 n
a i = r
, i - n 1 - n 2 - n 3 - n 4 - 1
1 - q 5 5
где i = n 1 + n 2 + n 3 + n 4 + 1,..., n 1 + n 2 + n 3 + n 4 + n 5.
В формулах (3–5) q 1, q 2, q 3, q 4, q 5— знаменатели геометрической прогрессии; n 1, n 2, n 3, n 4 — числа разбиений поверхностей на участки на двух сторонах электродов: n 1 и n 3 для электрода 1 на верхней и нижней сторонах, n 2 и n 4 для электрода 2 на верхней и нижней сторонах; n 5 — для экрана 3.
Моделирование поля датчика осуществлялось в трехслойной среде:
£1 , если b + h' < z < 2 b + h ',
£ ( z )= < £ 2, если b < z < b + h ',
£ 1 , если 0 < z < b .
Наведенные на границе раздела слоев связанные заряды учитывались с помощью метода зеркальных отображений. Они заменялись сосредоточенными зарядами, отраженными от границы раздела слоев. Коэффициенты пропускания β12 , β21 , коэффициенты отражений λ12 , λ21 и коэффициент двойных отражений γ вычислялись согласно [2]:
, _ 2£ 2 „ _ 2 £ 1 ; _ £ 1 - £ 2
' 12 = / \ , P 21 = / \ , ^ 12 = ,
( £1 + £ 2 ) ( £1 + £ 2 ) £1 + £ 2
^ 21 =
£ 2 £ 1
£ 1 + £ 2 ’
Y =
£ 2 £ 1 I
.
V £ 1 + £ 2 у
Поле датчика создается зарядами каждой пары электродов зеркально-симметричной конструкции, их отражениями, а также наведенными зарядами экранов 3 и 4. С целью сокращения записи для потенциалов точек xj , лежащих на поверхности электродов, была введена функция
W i( x j , ф ) =
= ^ j^Jt)in^(2rm +1 + x )2 + ф2 J [(2rm -t + x)2 + ф2 J[(2rm +t - x)2 + ф2J [(2rm -t - x)2 + ф2Jdt + m=i a 2 j j j j
+ / — ( t )in [ ( t - x j )2 + ф 2 ][ ( t + x j )2 + ф 2 ] , i = 1,..., П 1 + ... + n 5 , j = 1,..., n + ... + n 5 , (8)
αi где координаты точек xj на поверхности электродов определяются выражением xj = (aj + Pj)/2; N — число секций слева и справа от центральной секции; αi , βi — границы участков интегрирования заряда, создающего поле в точке xj .
В этом случае выражения для потенциалов точек на поверхностях электродов центральной секции, обращенных к контролируемому материалу (0 < x j < r 0, r1 < x j < r , z = b + d ), запишутся в виде:
n 1 + ... + n 4 + 2 n 5 T
+ Z Z[Yse12Wi(xj, b + (2s +1)h'- d)+ i=n1 +...+n 5 +1 [ s=0
+ ^Х21Р12^1(xj , b + (2s +1)h' + d)] + n + n 2
z i=1
T
V i ( x j , 0) + Z [ Y^W i ( x j , 2 d +2 sh ' ) + s = 0
+2 Yv i ( x j , 2( s + 1) h ' )+Ys ^2iWu ( x j ,( 2 s + 1) h ' + h ) J
П ] + ... + n 4
+ z
i = n j + n 2 + 1
(1+ 2 21) W , ( x j , d ) +
T
+ Z [ Y s (1+ ^ 21 ) W i ( x j , 2 s h ' + d ) + s = 1
2 n 1 + 2 n 2 + n 3 + n 4 + 2 n 5 T
+ Z Z[YsWi(xj, h + 2sh‘) + i = n1 +...+n4 +2 n 5 +1 [ s=0
+2 Ys^ 2 1 W , ( x , , (2 s + 1) h ') +
+ Ys + 1 ^ 21 W , ( x j , (2 s + 1) h ' + 2 d ) ] +
2( n 1 + ... + n 5 ) T
+ Z Z[ys (1+Х21Ш. x,, h+d+2 sh ‘)+ i =2 n1 +2 n 2 + n 3 + n4 +2 n 5 +1 [ s=0
+( Ys + Л 2з y s - 1) (1+ 2 21 ) v , ( x , , 2 s h '- d ) ]
+
+ ( Ys + 1+ 2 21 Y s ) W i ( x , , (2 s + 1) h ‘+ d ) ]
n ] + ... + n 5 T
+ Z Z[Ys-1221в12^,(xj , 2sh' + b - d) + i = n1 +...+ n4 +1 [ s = 1
+ YP vi Wr ( x , , b + 2 s h ' + d ) ] +P 12 W ( b + d )
= - £ 2 £ 0 2nV ( x , ), j = 1,..., n 1 + n 2 . (9)
Для потенциалов точек на поверхностях электродов, обращенных к подложке (0 < xj < r0, r1 < xj < r, z = b ):
' 1 + n 2
T
E E [ y s ^ 21 (1 + Л 21 )^ i ( x j ,(2 s + D h' - d ) +
i = 1 L s = 0
Ys (1+ 2 21 ) v , ( X j , 2 sh ' + d ) ]
+Yse2X V i ( X j , ( 2 s + 1) h ‘ + b - d ) 1
+
+
2( n 1 + ... + n 5) T
+ E ElYse^ vi( Xj, i =2 n1 +2 n 2 + n 3 + n4 +2 n 5 +1 — s=0
( 2 s + 1) h ' + b ) +
n + ... + n 4
+ E (1+Л21) Vi(Xj , 0) + i = n1 + n2 +1 L
T "
+ E Ys ( l+ ^ 21) 2 2 21 V , ( X j , 2( s + 1) h ' ) + s = 0 ]
n 1 + ... + n 5
+ E e12Vi(xj , b)+ i=n1 +...+n 4+1 -
+ E (1 + ^ 21^ ^ 21 Ye 12 V i( X J , 2( s + 1) h + Ь ) + s = 0 ]
n 1 + ... + n 4 + 2 n 5 T
+ E E Yse12(1 + ^21) Vi(XJ , (2 s + 1)h'+ b) + i=n1+...+n 5 +1 — s=0
2 n 1 + 2 n 2 + n 3 + n 4 + 2 n 5 T
+ Y s e 21 V i ( X j , b +( 2 s + 1) h ') ] =
= - 8 1 8 0 2 nV ( X j ), (11)
где j = n 1 + n 2 + n 3 + n 4 + 1, ™ , n 1 + n 2 + n 3 + n 4 + n 5;
T — число отражений.
С учетом того, что общий заряд системы равен нулю
+ E
E l z ( i + ^ 21 x ( x j , (2 s + 1) h ' - d ) +
i = n + ... + n 4 + 2 n 5 + 1 — s = 0
+ Ys (1 + X21) v i ( X j , (2 s + 1) h ' + d ) ]
+
2( n + ... + n 5 )
+ E
T
E Ys (1 + 2 ) V (X j , (2 s + 1) h ')
i = 2 n + 2 n 2 + n з + n 4 + 2 n 5 + 1 — s = 0 ]
= - 8 2 8 0 2 nV ( X j ), j = n , + n 2 + 1, ™ , n + n + n 3 + n 4. (10)
Для потенциала V ( xj ) точек экрана (0 < x j < r , z = 0 ):
n 1 + n - 2 -
E E [ y Z v X X j ,2 s h ‘+ b + d ) +
T
s = 1
_ s = 0
+Y sHj-^.-- V i ( X j , b + 2 s h '- d ) ]
+
n + ... + n 4
+ E в2^,(Xj , b) + i = n1 + n2 +1 L
T"
+E(Ys + 221 Ys-1)^VXXj, b + 2sh')
s=1
r 0
J ( ^ 11( t ) + ^ 12( t ))d t +
+ J ( CT 21 ( t ) + CT 22 ( t ))d t + J CT 3 ( t )d t = 0, (12)
r 1 0
составлялась система n1 + ... + n 5 + 1 интегральных уравнений. Ее решением являются дискретные значения функций распределения поверхностных зарядов σ 11 i , σ 12 i , σ 21 i , σ 22 i , σ 3 i и потенциала V 2 .
Для верхней пары электродов 1 и 2 (z = b + d ) частичная межэлектродная емкость C1B2 одной секции вычисляется n1 + n2
CB2 = L E ст21(x,)li /(V1 - V2);,(13)
i = n 1 + 1
для нижней пары n1 +..+ n 4/
(z = b ) CH = L E CT22(Xi)li (V1 - V2);(14)
i = n1 +...+n 3 +1/ частичная емкость одной секции между высокопотенциальным электродом 1 и экраном 3 C13 равна
n + ... + n 5
+ E i = n +...+n 4 +1 -
V i( x j , 0) + Z V 3 i ( x j , 2 b ) +
T
+ E в 12 в 21 Y^ VHX j , 2( b + ( s + 1) h ‘ )) s = 0
n + ... + n 4 + 2 n 5 T
+ E E Y s Z e 21 V i( X j , 2 b + (2 s + 1) h ‘ )
i = n + ... + n 5 + 1 L s = 0
+
+
2 n + 2 n 2 + n 3 + n 4 + 2 n 5 Г T
+ E i=n +...+ n4 + 2 n 5 +1
E l / s l^V X X j , (2 s - 1) h ' + b - d ) +
_ s = 0
n 1 + ... + n 5 /
C 13 = L E ст з ( x , ) l i ( V 1 - V 2 ) , l i = e i - a i . (15) i = n 1 + ... + n 4 +1 /
Межэлектродная рабочая емкость равна C 12 = C 1 ^ 2 + C H . Так как частичная емкость C H является паразитной и присутствует в измерениях за счет потока поля в подложке, то ее необходимо минимизировать за счет выбора материала подложки, соотношения межэлектродного зазора r 1 - r 0 и толщины подложки b .
Программы для моделирования полей МЭНИК были написаны с использованием системы компьютерной математики MAPLE. Для визуализации поля выполнялся расчет эквипотенциалей электрического поля в воздухе ( ε 2 = 1). Расчет проводился
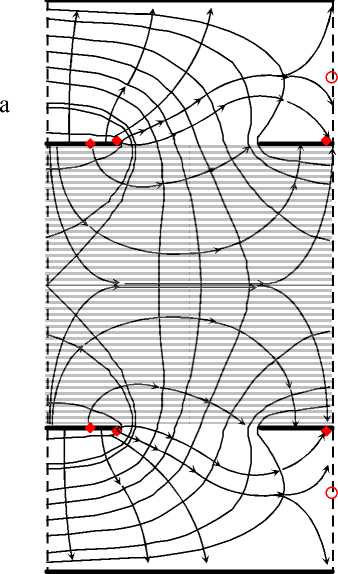
Рис. 2. Расчетные картины электрических полей. а — ЗСНИК; б — МЭНИК
1мм
б
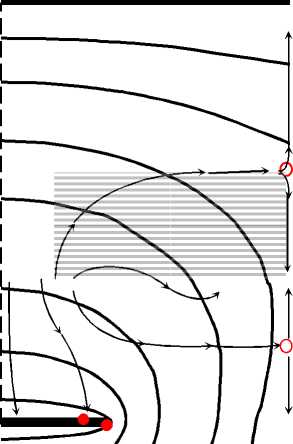
после нахождения дискретных значений распределения поверхностной плотности заряда <71 k (x), <72k (x), 73(x). Для конструкций ЗСНИК толщина подложек b равнялась 2 мм, толщина электродов µ = 35 мкм, размер секции r = 4мм, ширина потенциальных электродов r0 = r — r1 = 1 мм, одноименные электроды находились на расстоянии h= = 4 мм друг от друга. Диэлектрическая проницаемость подложки ε1 = 2.1. Расчетная картина электрического поля ЗСНИК представлена на рис. 2. Здесь же для сравнения показана расчетная картина электрического поля многосекционного экранированного накладного измерительного конденсатора МЭНИК [3]. Точками на поверхностях электродов выделены границы раздела потоков, замыкающихся на электроды "ощущения" 2 и экраны 3, 4, кольцами — на границах раздела секций. Координаты точек вычислялись посредством теоремы Остроградского—Гаусса. Координаты колец вычислялись через нахождение экстремума функции V(r, z) . Так как геометрические параметры электродов, межэлектродных расстояний и электрические параметры подложек одинаковы (рис. 2), то возможно сравнение основных характеристик датчика ЗСНИК и МЭНИК (глубина зоны контроля, рабочая межэлектродная емкость C12 и чувствительности к анизотропии диэлектрических свойств контролируемого образца). Из расчетных картин электрических полей видно, что глубина контролируемой зоны для МЭНИК составляет менее половины межэлектродного зазора и равна 0.41 h', в то время как преобразователь ЗСНИК контролирует весь объем межэлектродного пространства h'. Различия касаются и ширины зоны контроля. Для ЗСНИК ширина зоны контроля составляет ширину секции r , для МЭНИК 0.81 r . На рис. 2 рабочие области контроля для ЗСНИК и МЭНИК затонированы. В силу того что рабочие области контроля преобразователей ЗСНИК и МЭНИК различны, то значение рабочей емкости ЗСНИК выше значения рабочей емкости преобразователя МЭНИК. Для рассматриваемых конструкций на единицу длины электродов расчетные емкости соответственно составили C1 = = 1.248 пФ/м, C2 = 0.495 пФ/м. Это дает ЗСНИК преимущества над преобразователем МЭНИК, имеющим те же значения геометрических размеров.
Моделирование ЗСНИК: экспериментальные результаты
Выбор шагов разбиения поверхности электродов и экранов для заданного числа участков n 1 + ... + n 5 + 1, проверка сходимости численных расчетов емкости ЗСНИК с точными проводились для частного случая однородной среды ( ε 1 = ε 2 =1), когда зеркально-симметричные МНИК совмещены ( h = 0.001), а толщина электродов бесконечно мала ( d = 0.001 мм). Такая конструкция описана в работе [4]. Значения емкостей для нее вычислялись методами конформных отображений и непосредственного определения напряженности электрического поля. Расхождения в вычислении межэлектродных емкостей составляют менее 0.03 %.
Составные части преобразователя ЗСНИК были выполнены из двустороннего фольгированного фторопласта толщиной b =2.00 мм, толщина фольги (электродов) d = 0.035 мм. Для двух МНИК, входящих в конструкцию ЗСНИК, длина электродов L = 25 мм, число секций N = 6 было одинаково. При изготовлении электродов МНИК химическим травлением фольгированного фторопласта не удалось выдержать все размеры строго. С помощью микроскопа проводились измерения геометрических размеров всех электродов двух МНИК. Затем находились средние значения геометрических размеров электродов для каждого МНИК, вычислялась металлизация W поверхности МНИК (металлизация поверхности датчика — часть поверхности, занятая металлическими электродами либо иным проводящим материалом), проводились расчеты. Экспериментальные результаты и результаты численных расчетов представлены в таблице. Точность численных расчетов для частного случая разнесения МНИК h ^ да достаточно высока. Ошибка расчета емкостей составила менее 2.5 %. Для собранной конструкция развернутого ЗСНИК (МНИК лежат в одной плоскости) за счет соединений была внесена дополнительная емкость, она составила 0.041 пФ. При расчете относительной ошибки ее значение вычиталось из емкости ЗСНИК. Результаты численных расчетов и измеренной емкости ЗСНИК в случаях, когда h = = 2.8 мм и h =1.6 мм, представлены в таблице. Относительная ошибка расчета составила менее 4.5 %.
ВЫВОДЫ
Созданная модель носит общий характер, включает в себя модели многосекционных накладных измерительных конденсаторов. Модель позволяет проводить обоснованный выбор конструкции и параметров электроемкостных преобразователей, определять метрологические характеристики измерительного устройства, решать вопрос технической осуществимости поставленной задачи. Численные расчеты не требуют серьезного компьютерного обеспечения. Расчеты выполняются
Сравнение расчетных и измеренных значений емкостей преобразователей ЗСНИК и МНИК, входящих в конструкцию ЗСНИК


