Математическая модель зеркальной системы обсерватории "Миллиметрон" и описание метода предварительного обмера телескопа в рамках данной модели

Введение. Одним из основных направлений развития бортовых космических технологий является создание многозональных высокоапертурных зеркальных телескопов, обеспечивающих сбор и обработку информации в диапазонах спектра излучения от рентгеновского до миллиметрового. Примером этого служит проект космической обсерватории «Миллиметрон» (Спектр-М), рассчитанный для работы в миллиметровом и дальнем ИК диапазонах (70 мкм – 10 мм) с 10-метровым охлаждаемым (~4,5 K) криогенным телескопом [1–3]. Главной проблемой создания крупных телескопов является обеспечение качества изображения, что в свою очередь, требует разработки высококачественных и высокоточных методов контроля формы составных элементов их зеркальной системы [4–6]. В [7] представлен обзор состояния и тенденций развития космического телескопостроения за рубежом. Изложены результаты проводимых в ряде ведущих стран работ по проектированию и строительству оптических систем наблюдения за космосом. Рассмотрены находящиеся на орбите и строящиеся большие оптические телескопы с составными и гибкими зеркалами, управляемыми активными системами с целью устранения деформаций на всех этапах изготовления и эксплуатации.

Создание различных систем контроля формы составных элементов таких телескопов требует разработки математических моделей и алгоритмов работы данных контрольных систем [8–16]. В частности, в [8] изложена модель процесса юстировки составных зеркал высокоапертурных телескопов. На основе введенного понятия разностной поверхности с использованием разработанных алгоритмов геометрического и оптотехнического позиционирования зеркальных сегментов получены соотношения для оценки точности юстировки составных зеркал. В [16] кратко представлены методы юстировки и калибровки информационно-измерительных систем на борту космических аппаратов оптико-электронного и радиоэлектронного наблюдения.

Описываемая в настоящем сообщении система контроля зеркальной системы обсерватории «Миллиметрон» (СК ЗС) и не имеющие аналогов математическая модель и алгоритмы ее работы создаются для работы в составе бортового комплекса научной аппаратуры обсерватории «Миллиметрон» и рассчитывается на работу в условиях космического пространства. СК ЗС предназначена для контроля качества зеркальной системы (ЗС) космического телескопа и использования данных, получаемых СК ЗС в качестве сигналов «обратной связи» для предварительной настройки и юстировки оптической системы телескопа в космическом пространстве. В [17] на базе созданной математической модели описано моделирование работы бортового 3D-сканера при предварительном обмере зеркал обсерватории «Миллиметрон» с использованием оптических контрольных меток на поверхности зеркал. Настоящее сообщение посвящено описанию и анализу возможностей самой математической модели, применяемой в СК ЗС.

Основные положения и требования. Оптическая схема зеркальной системы обсерватории (телескопа) «Миллиметрон» приведена на рисунке.

Телескоп может быть представлен в виде физической модели, состоящей из множества оптических отражающих поверхностей (ОП) со стабильной формой. Совокупность всех ОП телескопа назовем зеркальной системой телескопа (ЗС). Примерами таких ОП являются (см. рис.): вторичное зеркало (ВЗ); переключающее зеркало (ПЗ); любая из панелей (фрагментов) многоэлементного параболоида главного зеркала (ГЗ).

Глобальная система координат (ГСК) телескопа определяется положением начала координат и координатными осями. Вершина параболоида главного зеркала (ГЗ) принимается за начало ГСК, в предположении идеальной формы параболоида ГЗ. Вектор оси X ГСК направлен вдоль оси параболоида ГЗ от его вершины в направлении вторичного зеркала (ВЗ). Вектор оси Y от центра переключающего зеркала (ПЗ) в сторону фокуса приемника, обозначенного как F 2 на рисунке. Ось Z однозначным образом дополняет оси X, Y, образуя полный ортогональный базис из векторов X, Y, Z ГСК, при котором ГСК является правой системой координат.

Однозначное положение каждой ОП как поверхности твердого объекта в пространстве определяется:

– выбранной базовой точкой на твердом объекте, содержащем ОП. Положение этой базовой точки объекта определено ее координатами в ГСК;

– тремя углами поворота объекта с ОП относительно его базовых осей в ГСК (углы Эйлера).

В итоге, положение каждой ОП в модели телескопа задается 6-ю параметрами – тремя углами поворота объекта, а затем радиус-вектором смещения базовой точки объекта в ГСК.

Знание положения каждой ОП телескопа по ее (6-и или иному достаточному количеству) собственных параметров (степеней свободы) означает, что геометрия (или конфигурация) всей ЗC телескопа точно и однозначно определена в рамках данной модели. В таком случае возможна оценки его оптического качества телескопа и его последующая настройка.

Обозначим полный набор параметров, описывающий положение всех ОП телескопа, как вектор (набор параметров) Х . Компоненты вектора содержат все параметры каждой ОП телескопа в его заданном состоянии. Так, например, если бы мы использовали в конструкции только 3 ОП, каждая описываемая 6-ю параметрами, то вектор Х состоял бы из 18 значений.

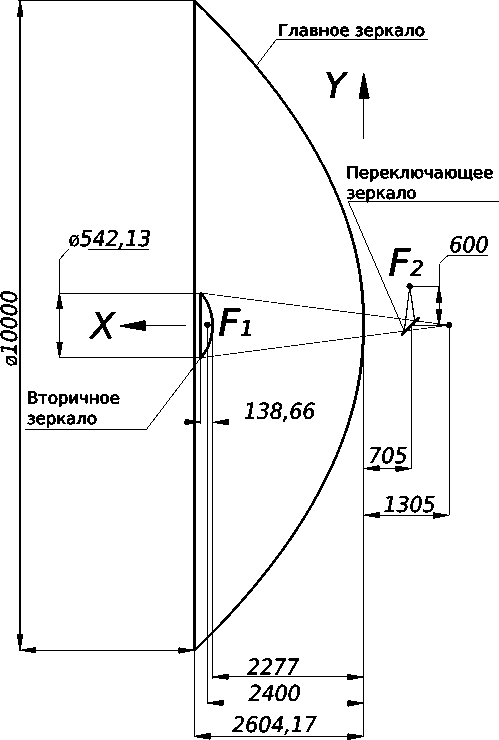
Оптическая схема зеркальной системы обсерватории «Миллиметрон». Расчетные характеристики: главное зеркало (ГЗ) – параболическое: радиус кривизны при вершине R ГЗ = 4800 мм; диаметр главного зеркала D_ГЗ = 10000 мм. Вторичное зеркало (ВЗ) – гиперболическое: R_ВЗ = – 254,7337 мм; D_ВЗ = 542,13 мм.

Расстояние между ГЗ и ВЗ – 2277 мм. Эквивалентное фокусное расстояние – 70000 мм. Расстояние от ВЗ до фокальной плоскости – 3582 мм. Квадрат эксцентриситета ВЗ е2= 1,147452

Optical diagram of the mirror system of the Millimetron Observatory. Estimated characteristics: main mirror (MM) – parabolic: curvature radius at the top of the R MM is 4800 mm; The diameter of the main mirror of the D MM is 10,000 mm. Secondary mirror (SM) – hyperbolic: R SM – 254.7337 mm; Distance between MM and SM – 2277 mm. Equivalent focal length – 70,000 mm. Distance from SM to focal plane – 3582 mm. Square of the eccentricity of the SM e² = 1,147452

Обмер поверхности телескопа 3D-сканером, являющимся штатным элементом СК ЗС, является косвенным, так как не измеряет напрямую параметры вектора Х , но измеряет доступные для измерения геометрические величины, связанные с вектором Х . Поэтому задачей СК ЗС является определение вектора неизвестных параметров Х по косвенным измерениям, получаемым в результате обмера телескопа 3D-сканером. Для получения косвенной информации о геометрии телескопа в СК ЗС заложен 3D-сканер. 3D-сканер – это прибор, расположенный в «теплом отсеке» космического аппарата (КА), который может запускать тонкий измерительный (оптический) луч в ЗС телескопа через временное оптическое окно между «теплым отсеком» и «холодной зоной» и «наблюдать» за всеми ОП из точки F2.

На поверхностях обмеряемых ОП расположены оптические контрольные метки (КМ), которые могут быть обмерены лучом 3D-сканера. КМ представляет собой металлический шарик (или сферическое зеркало, с характерным диаметром не менее 10 мм).

3D-сканер состоит:

• –    из дальномерного канала (ДК), позволяющего измерять длину оптического пути между входным зрачком приемно-передающего объектива ДК и некоторой КМ ОП. Для этого к КМ, через последовательность ОП посылается измерительный луч, регистрируется его отражение назад и вычисляется оптическое расстояние между объективом 3D сканера и КМ;

• –    сканирующего зеркала (СЗ) 3D-сканера, задающего направление измерительного луча ДК для прицеливания на центр выбранной КМ.

Работа СК ЗС осуществляется следующим образом:

• –    выполняется обмер всех или подмножества КМ с использованием 3D-сканера. По каждой обмеренной КМ на выходе 3D-сканера формируются 3 канала измерения (с индексами m = 0, 1, 2): m = 0 – длина оптического пути ДК до КМ; m = 1,2 – два угла СЗ при точном прицеливании на КМ;

• –    в результате обмера множества КМ по ЗС телескопа получается набор измерений (по три измерения на каждую КМ), который обозначим как вектор Y ;

• –    известный (после обмера множества КМ) вектор Y будет использоваться для оценки и восстановления вектора неизвестных параметров телескопа Х .

Математическая модель, описанная ниже, дает представление, как связать неявные измерения КМ (оптических КМ) Y с неизвестными параметрами ОП телескопа Х .

Математическая модель. Положения всех ОП определяются вектором неизвестных параметров Х.

Пусть полное число неизвестных параметров телескопа по всем ОП (длина вектора Х) равно Р. Индекс индивидуального параметра: p = 0,...,P-1. В таком случае конкретное значе ние параметра из набора X = {xp} с выбранным индексом р обозначим как xp.

Поскольку положения КМ связаны с положением ОП, то мы можем ввести функцию измерения 3D-сканером положения КМ с индексом k, по каналу измерения m от вектора состояния телескопа Х как fm,k (X) = fm,k (x0, x1, "., xP-1 ).

Измерение 3D-сканером всех меток формирует известный вектор Y ( X ) = { f_{m k} ( X ) } .

Вектор Y (совокупность всех измерений КМ по всем каналам 3D-сканера) зависит от вектора Х (всех неизвестных параметров ОП). Функции измерений f_mk = f_mk ( X ) = = f_mk ( x ₀, x 1 , ..., x_P - 1 ) в зависимости от Х являются существенно нелинейными и определяются чертежами и текущей геометрией телескопа.

Поскольку при выводе космической обсерватории на орбиту и после раскрытия телескопа в рабочее положение, его геометрия искажается незначительно по отношению к его линейным и иным размерам, то нелинейные функции f_mk ( ) можно считать постоянными по отношению к МАЛОМУ изменению аргумента Х , описывающего состояние ЗС телескопа, что и было подтверждено в результате численных экспериментов.

В таком случае, функции f_mk ( ) можно считать известными и вычисляемыми по начальной конструкции телескопа в настроенном состоянии (на основе геометрических данных из конструкторской документации (КД) телескопа).

Подытожив, имеем следующее:

• –    положение телескопа однозначно определяется неизвестным вектором Х ;

• –    3D-сканер СК ЗС может обмерять положения КМ (оптические контрольные метки), значения которых описываются функциями f_mk ( X ) ;

• -    функции f_mk ( ) известны (вычислением по чертежам КД) и предполагаются постоянными (независимыми от малого изменения аргумента Х ).

На основе этих предположений будем решать обратную задачу, т. е. определим расстройку параметров ОП ( Х ) от их исходного (идеального) положения по результатам неявного обмера множества КМ ( Y ) 3D-сканером.

Постановка задачи. Пусть телескоп настроен, это соответствует настроенному положению всех его ОП, которые мы обозначим как вектор X = { X_p } , состоящий из параметров X_p . Сами параметры X_p настроенного телескопа потенциально могут быть обмерены в заводских условиях, однако в этой информации нет необходимости, как это будет показано ниже.

При настроенном состоянии телескопа СК ЗС выполняет обмер всех ее КМ к = 0,..., K - 1 при помощи 3D-сканера по всем каналам измерения 3D-сканера m = 0,1,2 . Создается массив начальных измерений Y = { f_mk } (для настроенного телескопа на Земле), который соответствует настроенному вектору параметров X ЗС:

fm * = f m , к ( X ) = f m , к ( x ), X 1 ,^, X P - 1 ) ,

c

Y = { f m , к ( X ) } .

Массив измерений настроенного телескопа Y запоминается. После вывода телескопа на орбиту и его раскрытия в рабочее положение, ЗС телескопа расстроена, поэтому в новом положении телескопа на орбите его параметры ОП X = { X_p } случайно смещены по отношению к исходному (настроенному состоянию) состоянию X = { X_p } :

x 0 = х 0 + А х 0 , х 1 = х 1 + А х 1 ,

или X = X + х ,

ˆ

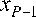
= ^х р - 1 ^{+ А х} p - 1

где ^х = { ^{А х} p } = { x p ^- x p }

– разностный вектор смещения параметров ОП. Полагается малость смещений х = {Ахp} = {Xp - Xp}.

Проведя обмер 3D-сканером СК ЗС всех КМ на орбите, получаем новый набор измерений положения КМ Y = { f_m , _к } :

^f m , к    ^f m , к ^{( X} )   ^f m , к ^{( X} 0 , ^X 1 ,-" ^X P - 1

Разница между полученными наборами измерений на орбите Y =

и настроенного в

заводских условиях Y = { f_mk } может быть линейно аппроксимирована (через дифференциал многомерной функции или многомерный ряд Тейлора) [18] как

ˆ

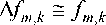
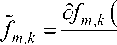
^х 0 , ^х 1 ,... ^х р - 1

a x 0

)

* А х 0 + ... +

^{d f} m , к ( ^X 0 , ^х 1,- ^X P - 1 )

д х_р - 1

* A x р - 1 ,

где

,     _ ^df m , k ⁽ x 0 , ^х 1,— x P - 1 )

частная производная функции измерения SD-сканера;

dm, k, p = axp x = X - X = {Axp} = {хp - xp} - вектор

изменения всех неизвестных параметров ОП (ЗС) от на строенного; y = Y - Y = {Afmk } = {fmk - fmk} - вектор изменения всех положений КМ обме ряемых SD-сканером.

В матричной записи выражение взаимосвязи измерений и изменения параметров будет выглядеть как

Af0,0 ^ ( d       d          d     X d 0,0,0      d 0,0,1     ... d 0,0, P-1 Af),1 d0,1,0       d 0,1,1     ...     d0,1, P-1 Afu d0,...,0       d0,...,1     ...     d0,..., P-1 Af0, K-1 d0, k-1,0   d0, k-1,1   ...   d0, K-1, P-1 Af1,o d1,0,0       d 1,0,1     ...     d 1,0, P-1 ' Ax0 ^ Af.,1 d1,1,0        d1,1,1      ...     d1,1, P-1 Ax 1 Af_ = ,,            ,,                  ,, d1,...,0       d1,...,1      ...     d1,..., P-1 • ... или y = H • x,        (6) Af\, K-1 d1, K-1,0    d1, K-1,1   ...   d1, K-1, P-1 ^Ах p-1 j Af2,0 d 2,0,0      d 2,0,1     ...    d 2,0, P-1 Af2,1 d 2,1,0       d 2,1,1     ...     d 2,1, P-1 ... d 2,...,0       d2,...,1     ...     d2,..., P-1 ,Af2, K-1) 4 d 2, K-1,0   d2, K-1,1   ...   d 2, K-1, P-1J где x = {A =p }=X - X - неизвестный вектор смещения параметров всех ОП, который надо вос- становить; y = {Afmk } = Y - Y' - вектор разницы измерений КМ (на орбите по отношению к измерениям в настроенном телескопе в земных условиях); H = {d(m k)p} - расчетная матрица частных производных, связывающая измерения КМ и неизвестные параметры модели ЗС телескопа (далее - дизайн-матрица).

Переформулируем задачу следующим образом: Определить изменения положения ОП от идеального настроенного x = { A x_p } = X - X по изменению положения КМ на орбите от их идеально настроенного y = { A f m _k } = Y - Y .

При этом известна матричная зависимость (прямая задача) y = H • x, где H - вычисляемая по чертежам постоянная дизайн-матрица (6). Необходимо решить обратную задачу: X = x (H,y).

Решение задачи. Определим вектор первичных параметров (смещений) ЗС телескопа.

Первичные параметры смещения - это параметры телескопа, которые показывают, насколько тот или иной компонент ЗС смещен относительно своего исходного состояния (когда телескоп настроен в заводских условиях): x 1 . Длина вектора здесь определена по количеству — p 1,1

описываемых им параметров/ компонент. Так p 1 - количество параметров вектор x 1 описы- — p 1,1

вает. Здесь и далее примем обозначение под матричной переменной   - означающее, что над

.-..

k, m скобкой – матричный элемент, имеющий k строк и m столбцов. Тем самым x1 – это вектор— p1,1

столбец длиной p1, или матрица размерности p 1 х 1 элемент.

Для полностью настроенной ЗС телескопа все параметры не смещены, т. е. равны нулю и, тем самым, все компоненты вектора x ₁ равны нулю.

— p1,1

Определим вектор измерений (смещений) y телескопа, который создается при обмере —¹ n ,1

(выполняемом СК ЗС) всех или подмножества КМ ЗС телескопа: y . — n ,1

Определим вектор шума измерений _ε телескопа, который создается при обмере (выпол- — n ,1

няемом СК ЗС) КМ ЗС телескопа: _ε . — n ,1

Определим первичную дизайн-матрицу H ₁ , как матрицу, характеризующую модель ЗС '

n , p ₁

телескопа и связывающую первичные параметры смещений x ₁ , вектор измерений y и шум

—— p1,1

измерений ε в одном уравнении: — n,1

У = H1 • Х1 + $ . — — n,1    n,p1 p1,1 n,1

Матрица преобразования системных параметров в первичные параметры . Первичные параметры смещений x ₁ непосредственно соотносятся положениям ОП, таким как панели ГЗ, — p 1,1

ВЗ и т. п. Системные параметры – это параметры, которые имеют обобщающую природу и могут влиять на группы первичных параметров. По сути это многомерная замена переменных. Обозначим системные параметры как вектор x . Число системных параметров или компонен- p ,1

тов вектора есть p . Чтобы математически формализовать преобразование обобщения парамет- ров, введем матрицу преобразования системных параметров в первичные параметры Ν та— , p1,p кую что x1 = N • x . Имеем:

^— 1 p 1, p p ,1

У = H1 • Х1 + $ = H1 —  ^— —     —

n ,1 n , p 1 p 1,1

• N • x + $ =

— —

_p 1 р 1, р p ,1

—

x ₁ — p 1

H — n , p —

— 1 • N n , p 1 ^{p 1, p}

• x + $ . —   — p,1    n,1

Поэтому дизайн-матрица H (с применением системных параметров) может быть выражена n,p как H = H1 • N . В таком случае связь измерений и системных параметров может быть выра-n, p "1 p 1, p жена формулой y — n,1

= H • x + £ . — —  — n,p  p,1    n,1

Случайный вектор изменения положения ОП x можно характеризовать его ковариацион- p ,1

ной матрицей [19] S = ST = Xkk • xm У Если мы полагаем, что параметры, составляющие p,p p,p вектор x , взаимно независимы, имеют нулевое среднее, тогда ковариационная матрица упро-p,1

щается и становится диагональной:

2 " 0 0 01 = S T = 0 -2 0 0 S — S' 0 0 0 p,p p,p 0 0 0 „ 2 V p 17 p, p

где стандартное отклонение индивидуального параметра с нулевым средним определяется как

^- k = 7( ^x k "^xk)   ^k = 0, ..., Р ^{- 1.}

Поскольку измерения разных КМ всегда независимы друг от друга, то сам вектор шума измерений 3D-сканером £ имеет диагональную ковариационную матрицу n,1

2 Y0 0 0 0 ' Y = Y T = 0 Y2 0 0 S n,n n,n 0 0 ... 0 V0 0 0 Y 2-1 > n,n состоящую из векторов стандартных отклонений измерений у , где Yk = ^еk • еk ^.

n,1

Так, если имеются две КМ, пространственно близко расположенные в ЗС, то они имеют близкие по значению (практически одинаковые) систематические ошибки в каналах 3D-сканера, при их обмере. В таком случае применение дифференциальных измерений КМ, т. е. попарная разница расстояний или углов каналов 3D-сканера до этих КМ, существенно снизит систематическую ошибку измерения расстояний или углов 3D-сканера.

Чтобы формализовать такое преобразование общим способом (в виде линейной комбинации измерений), вводим матрицу преобразования первичных измерений D . Получаем новую заме- ну переменных, переводя первичные измерения y в дифференциальные и , как u = D • у. m ,1         m ,1 m, n nj

S n,1

Вводим эквивалентную дизайн-матрицу G связи системных параметров с дифференциальными m,p измерениями: G = D • H . Тогда u = G • x + X , где эквивалентный шум дифференциального m,p m,n n,p             m,1 m,p p,1 m,1

измерения X при этом будет выражен через исходный шум первичного измерения £ m,1                                                                                                                                              n,1

как X = D • £ .

S S S m,1    m,n n,1

*------v------'

λ S m,1

Ковариационную матрицу дифференциального шума измерений можно выразить как

U = U ^T = cov X = cov D • £ -            -        - -

v m ,1 7

-

V m , n n ,1 7 m , n

( ^

= D • COV £

-

• DT ^-

V n ,1 у   n , m

= D • Y • D ^T .

- - -^

m , n n , n n , m

Решение обратной задачи. Имеется выражение u = G • x + X , связывающее неизвестные m ,1 m , pp ,1 m ,1

системные смещения параметров ЗС x с вычисляемыми ( известными) дифференциаль- p ,1

ными измерениями КМ u . При этом эквивалентная дизайн-матрица G - вычисляема (из-m,1                                                                    m,p вестна) по известным D и H , где X - модифицированный вектор шума дифференциальных m,n     n,p         m,1

измерений. Он имеет известные статистические свойства, такие как нулевое среднее и вычисляемую (известную) ковариационную матрицу U = - = D ' Y ' DT • Напомним, что S - из-m,m m,m m,n n,n n,m                           p,p вестная ковариационная матрица разброса неизвестных параметров ОП x , характеризующая p,1

их первоначальный разброс/ расстройку ЗС.

По известным u , G , U , S необходимо найти наиболее точное решение уравнения m,1 m,p m,m p,p u = G • x + X , т. е. найти вектор неизвестных системных параметров x . -  - -  -- m,1 m, pp,1 m,1

Для решения задачи ищем матричный решатель (матрица) F такой, что оценка x неиз-p,mp вестного вектора системных параметров x по дифференциальным измерениям u есть p,1

x = F • u .

• --

p ,1 p , m m ,1

При поиске матрицы F , необходимо подобрать ее таким образом, чтобы отклонение p , m

S x = x - x истинного смещения x и его найденной оценки x было минимально в статисти-

• — - -                    -                       -

• p,1 p,1 p,1                                         p,1                                               p,1

ческом смысле. Определим это как

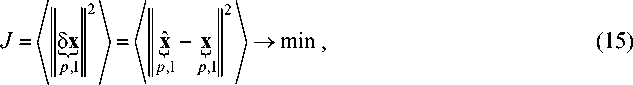
где ||a|| = ^ a k - норма вектора; ( ) - среднее значение от случайной величины. k

Опуская длинные промежуточные выкладки, приводим окончательную формулу для опти- мального решателя:

F = - p,m

г ^

G • S v m , p p , p у

T

G • S • G ^T

- - ^-^

V m , p p , p p , m

у

+ U m, m 7

p , m

m,m где (...)+ - псевдообратная матрица [20].

Анализ ошибок восстановления параметров. Случайный вектор ошибки восстановления неизвестных параметров S x - это разница между истинным неизвестным вектором системных p ,1

параметров состояния ЗС после вывода на орбиту x и оценкой x этого вектора, полученной p ,1                       p ,1

по дифференциальным измерениям с использованием формулы (16):

S x = x - x .                                       (17)

v v v p ,1 p ,1 p ,1

Ковариационная матрица для вектора ошибки

S x v p ,1

восстановления параметров по результа-

там вычислений имеет следующий вид:

А = cov S x

v p,p

V p,17

= Q • v

S • Q^T