Математическая оценка влияния факторов на прямые расходы на производство продукции ООО "Царь-хлеб" с помощью корреляционно-регрессионного анализа

Автор: Сырисько Я.А., Рожкова М.Г.

Журнал: Теория и практика современной науки @modern-j

Статья в выпуске: 1 (19), 2017 года.

Бесплатный доступ

В статье математически оценивается влияние различных факторов на прямые расходы производства с помощью корреляционно-регрессионного анализа. С этой целью исследуется степень корреляционной зависимости как между объясняющими факторами и результативным, так и мультиколлинеарность (зависимость между объясняющими факторами). В результате представлены выводы анализа и рекомендации по уменьшению по снижению прямых расходов на производство продукции ООО «Царь-хлеб».

Прямые расходы, математическая модель, производство, корреляционно-регрессионный анализ, мультиколлинеарность, статистика дарбина-уотсона, тест бреуша-годфри

Короткий адрес: https://sciup.org/140270176

IDR: 140270176

Текст научной статьи Математическая оценка влияния факторов на прямые расходы на производство продукции ООО "Царь-хлеб" с помощью корреляционно-регрессионного анализа

Корреляционно-регрессионный анализ является важнейшим методом многомерного статистического анализа – обширной области прикладной статистики, занимающейся установлением взаимосвязи случайных величин, в частности параметров технологического процесса, характеристик качества продукции, технико-экономических показателей и т.д. [1]

Исследуем степень корреляционной зависимости между переменными, используя исходные данные, приведенные в таблице 1.

Таблица 1 - Исходные данные для проведения корреляционно регрессионного анализа

Период	Прямые расходы на производство продукции (Y)	Стоимость активов (X1)	Коэффициент износа (X2)	Коэффициент автономии (Х3)
январь	86963,7	59630,00	0,32	0,31
февраль	93637,32	110315,50	0,35	0,27
март	96009,98	122450,21	0,56	0,26
апрель	95630,3	113511,34	0,55	0,26
май	93693	77187,71	0,50	0,29
июнь	91262,7	74640,52	0,47	0,32
июль	105163,04	88822,21	0,57	0,26
август	112693,36	96816,21	0,65	0,22
сентябрь	139692,6	131670,05	0,87	0,15
октябрь	135963,08	127456,61	0,77	0,16
ноябрь	123658	115921,39	0,67	0,19
декабрь	119885,92	102010,82	0,61	0,20
январь	134632,2	193820,57	0,73	0,12
февраль	143695,9	389579,34	0,81	0,10
март	147469,9	399811,17	0,89	0,09
апрель	143962	381819,67	0,79	0,15
май	139978,36	366928,70	0,67	0,18
июнь	133075,64	337574,41	0,54	0,19
июль	146329	391586,31	0,72	0,17
август	156369,3	442492,53	0,83	0,15
сентябрь	163029,7	461340,08	0,98	0,13
октябрь	162369,45	456265,33	0,87	0,14
ноябрь	155368,95	436593,62	0,75	0,15
декабрь	154774,6	397300,19	0,68	0,15

Для этого построим корреляционную матрицу, используя средства «Анализа данных». Корреляционная матрица приведена на рисунке 1.

Из корреляционной матрицы следует, что на прямые расходы на производство продукции (результирующий фактор) оказывают влияние все отдельные переменные факторы, т.е. стоимость активов, коэффициент износа и коэффициент автономииимеют корреляционную связь с прямыми расходами на производство. Так, связь между стоимостью активов и прямыми расходами равна 88,1%, что является признаком сильной прямой взаимосвязи между данными факторами. Взаимосвязь между коэффициентом износа и прямыми расходами равна 0,87%, что так же говорит о сильной прямой степени взаимосвязи. Степень зависимости между коэффициентом автономии и прямыми расходами на производство составляет 83,6% и является отрицательной, т.е. зависимость между факторами обратная и сильная.

Также можем отметить наличие корреляционной зависимости между объясняющими переменными, это может свидетельствовать о наличии в модели явления мультиколлинеарности.

Результаты регрессионного анализа тоже приведены на рисунке 1.

Так, 0,937 - это R2 - коэффициент детерминации, показывающий, что на 93,7% расчетные параметры модели, то есть сама модель, объясняют зависимость и изменения изучаемого параметра Y (прямые расходы на производство) от исследуемых факторов - стоимости активов (X1), коэффициента износа (X2) и коэффициента автономии (Х3). Коэффициент детерминации является показателем качества модели, и чем он выше, тем более статистически значима модель. Т.к., исходя из результатов анализа, коэффициент детерминации равен 0,37, что говорит о весьма высокой степени статистической значимости регрессионной модели.

Скорректированный на потерю степеней свободы коэффициент множественной детерминации равен 0,927 (92,7%).

	Прямые расходы на производство продукции (¥}	Стоимость активов (X1J	коэффициент износе (Х2)	коэффициент оетоно.иии
Прямые расходы на производство продукции	1
Стоимость а кти bob \|XL)	0,880967782	1
коэффициент износа \|Х2}	0,577298726	0,656802368	1
Коэффициент автономии (В)	-0,836271128	-0,64790303	-0,868543 966	1
вывод итогов
Регрессионная статистика
Множественный R	0,967763169
R-квадрат	0,936565551
Нормированный R-квадрат	0,9270503 84
Стандартная ошибка	6807,548153
Наблюдения	24
Дисперсионный анализ
	df	55	М5	f	Значимость F
Репрессия	3	13684358550	4561452883	98,42870002	3,78948-12
Остаток	20	925854237,2	46342711,85
Итого	23	14511212888

	коэффициенты	Стандартна я ошибка	г-статистика	Р-Зночение	нижние 95«6	Верхние 95%	Нижние 95.0%	Верхние 95.0%
Y-пересечение	106533,275	21191,58248	5,027150526	6,457418-05	62328,4087	150738,1414	62328,4087	150738,1414
Стоимость активов \|XL)	0,070187156	0,013997827	5,014146379	6,653198-05	0,040988199	0,0993 85112	0,040988199	0,099386112
Коэффициент износа [Х2}	42538,96829	17860,21736	2,381772149	0,027274263	5283,207813	79794,72876	5283,207813	79794,72876
Коэффи ци ент а втономи и [>	-127030,5309	50379,95726	-2,521449755	0,020281632	-23 2121,2733	-21939,78185	-232121,2799	-21939,78185

"Теория и практика современной

Рисунок 1 - Результаты проведения корреляционно-регрессионного анализа

"Теория и практика современной

Теперь перейдем к коэффициентам модели. Свободный коэффициент в математической модели равен 106533,28 - это коэффициент, который показывает, какими будут прямые расходы на производство продукции в случае, если все используемые в модели факторы (стоимость активов, коэффициент износа и коэффициент автономии) будут равны 0. Подразумевается, что это зависимость от других, неописанных в модели факторов.

Коэффициент весомости фактора Х1 (стоимость активов) в модели равен 0,07019.Данный коэффициент показывает весомость влияния фактора Х1 на Y, то есть сумма активов в пределах данной модели влияет на показатель прямых расходов на производство с весом 0,07019. Положительное значение показывает, что это влияние прямое, т.е. чем больше сумма активов, тем большепрямых расходов, как бы это ни было парадоксальным по смыслу.

Коэффициент влияния коэффициента износа на величину прямых расходов на производство, согласно модели, равняется 42538,97. Значениетак же является положительным, что говорит о прямом влиянии на прямые расходы.

В свою очередь, коэффициент автономии, который в модели равен -127030,53, является отрицательным, т.е., согласно модели, увеличение коэффициента автономии будет способствовать уменьшению величины прямых расходов на производство.

Таким образом, в нашем случае прямые расходына производство продукции увеличиваются на 0,07019 тыс.руб. при увеличении стоимости активовООО «Царь-хлеб» на 1 тыс.руб. при неизменности остальных факторов модели. Прямые расходы на производство увеличиваются на42538,97тыс.руб. при увеличении коэффициента износа на 1 ед., если не брать во внимание остальные факторы модели. При увеличении коэффициента автономии ООО «Царь-хлеб» на 1 ед. прямые расходы на производство продукции будут уменьшаться на 127030,53тыс.руб. при неизменности остальных факторов модели. Случайное отклонение для коэффициента при переменной Х1 составляет 0,014; при переменной Х2 – 17860,22; при переменной Х3 – 50379,96; для свободного члена –21191,58.

Соберем рассчитанные коэффициенты в модель:

Y = 0,07019*Х1+42538,97*Х2 - 127030,53*Х3+106533,28

Собственно, это и есть линейная регрессионная модель, которая для исходных данных выглядит именно так.

t-статистика рассчитывается путем деления коэффициента регрессионной модели на стандартную ошибку. Исходя из значения t-статистики, можно судить о том, каким переменным фактором можно пренебречь в модели. Из таблицыкритериев Стьюдента следует, чтоt табличное в нашем случае равняется 2,06. Следовательно, если t-критерий одной из переменной по модулю будет меньше 2,06, то им можно будет пренебречь.

Таким образом, видим, что для свободной переменной t-критерий равен 5,027, для переменной Х1 – 5,014, для переменной Х2–2,382, для переменной Х3–-2,521. Можно сделать вывод, что все переменные модели являются значимыми, т.е. ими нельзя пренебрегать.

Р-значение – вероятность принятия нулевой гипотезы. В данном случае нулевая гипотеза заключается в том, что коэффициент регрессии равен нулю. Т.е. если принимается нулевая регрессия, это говорит о том, что соответствующий коэффициент в модели не считается статистически значимым. Будем считать допустимым значение 0,05.

Таким образом, принятие нулевой гипотезы по константе равно 6,46*10-5. Значение принятия нулевой гипотезы по константе меньше 0,05 (5%), значит константу в нашем уравнении будем считать статистически значимой. Далее для переменной Х1 (стоимость активов) вероятность принятия нулевой гипотезы равняется 6,65*10-5, что так же гораздо меньше 5%, следовательно, переменную Х1 тоже будем считать статистически значимой. Что касается переменной Х2, вероятность принятия нулевой гипотезы по переменной принимает значение 0,027. Значение хоть и ближе к 5%, чем в остальных переменных, но все-таки меньше допустимого значения, что говорит о статистической значимости переменно Х2 (коэффициент износа). При рассмотрении вероятности принятия нулевой гипотезы переменной Х3 (0,021) было так же выявлено, что она меньше 5%, т.е. коэффициент автономии является тоже статистически значимым для данной регрессионной модели.

Далее в таблице результатов показывают нижние значения оценочного коэффициента регрессии и верхние, т.е. мы имеем интервальную оценку значения регрессии с 5%-ным уровнем значимости.

Значение F-критерия (Фишера) равно 98,43. Нулевая гипотеза в данном случае заключается в том, что уравнение регрессии в целом статистически не значимо. В таблице справа от него представлен показатель значимости F, т.е. это значение вероятности принятия данной нулевой гипотезы, которое равно 3,79*10-12. Согласно критерию Фишера данная модель адекватна, т.к. уровень значимости модели меньше 0,00001, поэтому принять нулевую гипотезу в данном случае мы не можем.

Следующее, что мы должны выполнить – оценить остатки модели на явление автокорреляции, т.е. проверить, коррелируются ли между собой остатки модели. При выведении остатков модели можно увидеть предсказанное значение Y(прямых расходов) и остатки. Результаты проверки корреляции остатков модели представлены на рисунке 2.

ВЫВОД ОСТАТКА

№tiw Авен	J^vdaraowue ^W№W pOODd±l .•to лгоивияХтпео nnoSp.Yjpj /^	Doa™™u		k-tJ‘		^4
1	81951/Ю11	2012,139535	-	-	-1909/53327	2012,139535
2	95217/5833	-1905,5=5517	2591905/27	13119395/1	-9319,957913	-1909/53327
=	105339,5175	■9319,957915	97015957/5	67895135/1	-9535/95953	-9319,957913
	to5S 15,9999	■9535/95953	95305532,91	29991/1155	-= =57,5051=7	■9535/95953
5	97050,90511	■9357/05137	11273520/3	ЮОЮ532/	-115/595333	■9357/05137
6	92579,25953	-116/396853	13562/5732	10303032/8	919,9952073	-116/596853
7	104213/733	919,9952073	901555/052	1139521/15	913,13314	919,9952073
3	113611/131	918,15314	31=011/701	3133757,791	6255/7595	913,15314
9	133427/231	9195,1795=	39255995/1	51601739/	3512/00911	6255/7695
to	127330,5791	8512/00912	71175119/7	5503991,121	1100/11368	3512/00912
11	115557,9351	<100/11563	15312557/2	20553917/	9000/25972	1200/2 23 53
12	11:335,501	9000/23972	35005791,75	3610015/92	-1451/95531	9000/23972
23	159035/955	-1451/955/1	2111977/25	55571241,52	-12563/3957	-14512955S1
14	159051/391	-12363/3957	152991593,1	119130524/	-13332/3992	-12363/3957
	1513022399	-13352/3992	191333527,7	2141391/2	-4325/23203	-13352/3392
to	143237/231	-4325/23103	15710130,11	90579595/1	2051/30523	-4325/23 toS
17	137923/097	2051/50528	1222Ю9/59	10709165,11	3791/13137	1031 530=15
IS	129511/295	3751/13437	14169502/	2521922/4	3135/51365	=751,11=1=7
to	21239E/55	5455/51965	11305519/9	10775 5,7513	1391,572955	51/5/51965
20	154577,527	1991,572936	3995751,165	2035892,752	-1275,163225	1991,571936
21	251EO1/558	-1275,153225	1529016/51	10572231,72	1139/1905	-1275,153225
22	157550/= =5	1139/1905	20151255,19	53225735/1	13IS/2271	1139/1905
	150515,517=	^=31171.	23151399/5	125320,7239	to271,95B9	131= 01171
	14^55,5=01	1017^,9955	105368511,5	2=3027=0 55
Ятсп>	X	X	92230=451	6H3#4*4J
DW			•>S«	'54=4


	2
	0,555710395	2

pao-er -: "	з^тэзтаэ
T 4KT№I 4C4td	•>ti 4644

Рисунок 2 - Результаты проверки корреляции остатков модели

Для проверки остатков на автокорреляцию найдем значение статистики Дарбина-Уотсона по следующей формуле:

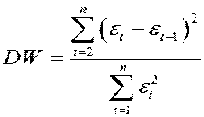
, где

- квадрат разностиостатков на i-тое наблюдение и на предшествующее ему наблюдение;

- квадрат остатков i-того наблюдения.

Так, значение статистики Дарбина-Уотсона, найденное с помощью данной формулы, равняется 0,6544.

По таблице определяем значащие точки dL и dU для 5% уровня значимости. Для k=3 и n=24: dL=1,2; dU=1,65 [2].

Так как DW

Проверим наличие автокорреляции, используя тест Бреуша-Годфри.

Тест основан на оценке корреляции между остатками модели, т.е. между и . Из построенной корреляционной матрицы видим, что коэффициент корреляции равен 0,656. Проверка значимости данного коэффициента производится по следующей формуле:

Т =

r*Vn-2

-i^ , где

Т – коэффициент Стьюдента;

r – коэффициент корреляции;

n – число степеней свободы [3].

Так, коэффициент Стьюдента равен 3,98. Данный коэффициент выше Т критического (3,98>0,063). Это говорит о том, что рассчитанный коэффициент корреляции является значимым, следовательно, мы не можем принять нулевую гипотезу, которая заключается в том, что коэффициент корреляции между остатками равен нулю. Таким образом, остатки модели коррелируют между собой, т.е. имеет место автокорреляция остатков модели.

Таким образом, как статистика Дарбина-Уотсона, так и тест Бреуша-Годфри показали наличие автокорреляции между остатками модели [4]

В результате проведенного корреляционно-регрессионного анализа можно сделать следующие выводы:

- регрессионная модель прямых расходов на производство продукции (Y=0,07019*X1+42538,97*X2-127030,53*X3+106533,28) статистически значима в целом;
- по итогам анализа t-критериев можно сказать, что коэффициенты регрессии статистически значимы;
- прямые расходы на производство продукции увеличиваются на 0,07019 тыс.руб. при увеличении стоимости активов ООО «Царь-хлеб» на 1 тыс.руб. при неизменности остальных факторов модели. Прямые расходы на производство увеличиваются на 42538,97 тыс. руб. при увеличении коэффициента износа на 1 ед., если не брать во внимание остальные факторы модели. При увеличении коэффициента автономии ООО «Царь-хлеб» на 1 ед. прямые расходы на производство продукции будут уменьшаться на 127030,53 тыс.руб. при неизменности остальных факторов модели.
- имеется зависимость между объясняемыми переменными (между стоимостью активов и коэффициентом износа - 68,7%, между стоимостью активов и коэффициентом автономии - 64,8% и между коэффициентом

износа и коэффициентом автономии – 86,8%). Это достаточно высокие значения, что говорит об их корреляционной зависимости, т.е. имеет место мультиколлинеарность;

- существует автокорреляция между остатками модели, установленная с помощью статистики Дарбина-Уотсона и теста Бреуша-Годфри, что может привести к ненадежности оценок, выводы по t- и F-статистикам, определяющим значимость коэффициентов регрессии и детерминации, возможно, неверны.

Таким образом, для уменьшения прямых расходов на производство продукции ООО «Царь-хлеб» следует принять во внимание следующие рекомендации:

1. Пересмотр метода начисления амортизации основных средств производственного назначения. Согласно учетной политики ООО «Царь-хлеб», предприятие использует линейный способ начисления амортизации, исходя из первоначальной стоимости и нормы амортизации, исчисленной исходя из срока полезного использования. Возможно, необходимо пересмотреть метод начисления амортизации с целью снижения коэффициента износа и более рационального включения в состав прямых расходов на производство.
2. Привлечение большего количества собственников с целью увеличения собственного капитала, т.е. собственных средств предприятия. Чем выше будет собственный капитал, а именно прибыль и меньше активы, тем выше коэффициент автономии. Это позволит повысить финансовую независимость предприятия и, как следствие понизить прямые расходы на производство продукции.
3. Понизить сумму заемных средств на предприятии, выплатив кредиты банка и другие заемные средства, что так же повысит значение
4. Закупка только необходимого сырья и материалов, а также своевременное использование закупленного сырья для изготовления продукции для минимизации порчи материальных ресурсов. Таким образом, при уменьшении активов будет происходить уменьшение прямых расходов на производство.

14 коэффициента автономии и понизит сумму прямых расходов на производство продукции ООО «Царь-хлеб».

Список литературы Математическая оценка влияния факторов на прямые расходы на производство продукции ООО "Царь-хлеб" с помощью корреляционно-регрессионного анализа

Метод корреляционно-регрессионного анализа [Электронный ресурс]. - Режим доступа: http://megaobuchalka.ru/5/5132.html
Статистика Дарбина-Уотсона [Электронный ресурс]. - Режим доступа: http://crow.academy.ru/econometrics/materials_/Tables_/DW-distr.htm
Построение эконометрических моделей, представленных различными типами временных рядов [Электронный ресурс]. - Режим доступа: http://www.managevation.ru/mvas-173-2.html
Видео урок решения в Excel задачи на построение модели множественной регрессии [Электронный ресурс]. - Режим доступа: http://easyhelp.su/subjects/ekonometrika_reshenie_zadach/video_urok_resheniya_v_excel_zadachi_na_postroeneie_modeli_mnozhestvennoj_regressii

Статья научная