Математические методы формирования многоалфавитных шифров замены

В статье рассматривается шифр многоалфавитной замены, основанный на интегральном преобразовании.

Постановка задачи

Шифры одноалфавитной замены (например, квадрат Полибия) не являются криптостойкими. Значительно надежнее шифры многоалфавитной замены (например, шифр Виженера). В этих шифрах каждому символу открытого текста ставится в соответствие не один, а несколько символов алфавита замены [1].

Представляетинтересразработкаисовершенс-твование криптостойких шифров многоалфавитной замены. Для создания таких шифров может быть использован различный математический аппарат, например, интегральное исчисление.

Разработка шифра многоалфавитной замены

В предлагаемом шифре каждый символ (буква, знак препинания, цифра) заменяется двумя вещественными числами. Эти два числа являются верхним и нижним пределами определенного интеграла. Значение интеграла используется для того, чтобы на приемной стороне по таблице замен определить, какому символу открытого текста соответствует вычисленное значение интеграла. Предполагается, что вид подынтегральной функции и конфигурация таблицы замен известны только доверенным лицам на передающей и приемной сторонах. В каждом сеансе связи таблица замен и подынтегральная функция определяются секретным ключом.

Рассмотрим порядок шифрования с помощью предлагаемого метода.

В данном сеансе связи из множества возможных видов выбирают некоторый конкретный вид подынтегральной функции:

b

I = J f ( x ) dx . (1) ^a

С помощью таблицы замен ставят в соответствие каждому символу алфавита открытого текста s _i определенный интервал вещественных чисел [c i ; d i ) .

Для шифрования некоторого символа s _i генерируют случайное число I i из интервала [c i ; d i ) . Затем из некоторого допустимого интервала [ k ; m ] генерируют еще одно случайное число, например, a _i (нижний предел интегрирования). С помощью формулы Ньютона-Лейбница

b

Jf (x) dx = F (b) - F(a) (2) a по известным значениям интеграла Ii и нижнего предела ai вычисляют значение верхнего предела bi .

По открытому каналу связи передают два числа a _i и b _i . На приемной стороне числа a _i и b _i используют для вычисления интеграла I _i . Так как вид подынтегральной функции на приемной стороне известен, то вычисление определенного интеграла не представляет труда. Полученное значение I _i используется для определения с помощью таблицы замен принятого символа s _i .

Поясним идею с помощью конкретного примера.

Пусть для шифрования (в соответствии с некоторым ключом) выбрана подынтегральная функция f ( x ) = x ² , то есть

b

I = ∫ x ² dx . (3) ^a

Далее формируют таблицу замен. При этом каждому символу открытого текста в соответствии с ключом ставят в соответствие своё значение интервала вещественных чисел. Приведем фрагмент подобной таблицы (см. таблицу 1). Затем шифруют открытый текст.

Предположим, что нужно зашифровать символ «В». Вначале в соответствии с таблицей замен формируют случайное вещественное число из интервала [ c ; d ) . Из таблицы 1 видно, что символ «В» может быть зашифрован любым вещественным числом из интервала [2; 3).

Допустим, что сгенерировано число I = 2,5 . Затем генерируют некоторое случайное число (нижний предел интегрирования). Пусть таким числом будет a = 3,2 .

Формула Ньютона-Лейбница (2) позволяет по известным значениям интеграла I и нижнего предела a вычислить верхний предел интегрирования. Для интеграла вида (3) верхний предел b вычисляют по формуле:

b = 3/3 • I + a ³ .                (4)

Подставляя значение интеграла I и нижнего предела a в (4), получают b = 3,428 .

Таким образом, в линию предают два вещественных числа: 3,2 и 3,428, которые представляют собой замену символа «В».

На приемной стороне эти два числа используют для вычисления интеграла (3). Полученное число I = 2,5 позволяет по таблице замен определить значение принятого символа (буквы). Очевидно, что в данном случае это будет символ «В».

Таблица 1.

Символы текста, s i	А	Б	В	Г	Д	Е
Интервалы замен, [ c ; d )	[0; 1)	[1; 2)	[2; 3)	[4; 5)	[5; 6)	[6; 7)

Замечания об округлении чисел

Объем шифрограммы и время ее передачи по каналу связи тесно связаны с разрядностью передаваемых чисел. Естественно, что разрядность чисел желательно уменьшать (не снижая криптостойкость). В этом случае потребуется выполнить разумное округление чисел. Из-за сделанных округлений в процессе шифрования могут произойти ошибки двух видов: принимаемый символ может быть воспринят (опознан на приеме), как соседний слева символ или как соседний справа символ (речь идет о таблице замен).

Рис. 1 поясняет, как могут возникнуть ошибки из-за неверного округления. На приеме буква «Б» может быть принята как буква «А», либо как буква «В». Округление значения интеграла I при шифровании не требуется, так как оно не передается по каналу связи. Поэтому разрядность этого числа может быть любой.

Округление первого сгенерированного предела интегрирования на передающей стороне не может сказаться на надежности дешифрации, так как по его значению вычисляется зависимый второй предел интегрирования. По этой причине первый сгенерированный предел можно округ- лять без всяких ограничений. Округление же зависимого предела (второго) должно происходить по определенным правилам.

Если интеграл генерируется в левой половине интервала замен, то предел округляется так, чтобы значение интеграла увеличивалось (чтобы на приеме не попасть в левый соседний интервал замен). Если интеграл сгенерирован в правой половине интервала замен, то округление ведется в сторону уменьшения вычисленного значения интеграла.

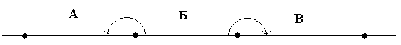
Рис. 1. Возможные ошибки на приемной стороне

Покажем, как с помощью рассмотренного метода может быть зашифрована фраза «ГДЕ АББА» (см. таблицу 2).

Прокомментируем полученные результаты. Следует обратить внимание на тот факт, что дважды встретившиеся в открытом тексте символы «А» и «Б» были зашифрованы разными парами вещественных чисел. Например, первая бук-

Таблица 2.

Текст Г Д Е А Б Б А I 4,3 5,11 6,8 0,12 1,4 1,785 0,85 a 3,98 12,3 0,11 6,36 2,43 8,2 1,5 b 4,235 12,334 2,732 6,363 2,647 8,226 1,81 ва «А» зашифрована парой чисел (6,36; 6,363), а вторая буква «А» – числами (1,5; 1,81).

Повторим шифрование, взяв прежнюю таблицу замен и новую подынтегральную функцию: f ( x ) = e . В этом случае верхний предел b вычисляется по формуле:

b = ln(e a +1) .

Результат шифрования приведен в таблице 3.

Сложность криптоанализа полученных шифровок состоит в том, что противник не знает, каков вид использованной таблицы замен, и какая использована подынтегральная функция. В реальной таблице замен символы располагаются в псевдослучайном порядке (не в алфавитном порядке). Кроме того, символы открытого текста (в том числе и одинаковые) в передаваемом сообщении не шифруется одинаковыми числами. Это

Таблица 3.

Текст Г Д Е А Б Б А I 4,85 5,82 6,07 0,52 1,59 1,03 0,45 a 0,6 1,2 2,1 1,85 2,43 4,71 0,824 b 1,898 2,213 2,656 1,929 2,561 4,719 1,004 обеспечивается генерацией в процессе шифрования каждого символа двух случайных чисел (значение интеграла и одного из пределов интегрирования). Заметим, что при генерации случайных чисел целесообразно использовать генераторы с равномерным распределением.

Не всякая подынтегральная функция может быть с одинаковым успехом использована при шифровании. Так тригонометрические функции вносят ограничения на значения подынтегральной функции и пределов интегрирования. Эти ограничения делают такую криптографическую систему сложно реализуемой.

В таблице 4 приведены примеры простейших подынтегральных функций и определены границы их использования для шифрования.

Таблица 4.

Подынт. функция .f ( x )	Вычисление нижнего предела a по известным I и b	Ограничения по b	Вычисление верхнего предела b по известным I и a	Ограничения по a
x	a = bb2 - 2 • I	b 2 -2⋅I≥0	b = V2 • I + a 2	2 • I + a 2 >  0
x 2	a = Vb3 - 3. I	-	b = V 3 • I + a 3	-
x3	a = 4/b4 - 4 • I	b 4 -4⋅I≥0	b = 4 4 • I + a 4	4 • I + a 4 >  0
x 4	a = 5/ b5 - 5 • I	-	b = V5 • I + a 5	-
sin x	a = arc cos(cos b + 1 )	cosb +I ≤ 1	b = arc cos(cos a -1 )	cos a - I ≤ 1
1/ x	a = exp( In b - 1 )	b>0	b = exp( I + In a )	a>0
C x	a = log c ( C b - 1 • In C )	C b >  I • In C	b = log C ( I • In C + C a )	I • In C + C a >  0
e x	a = ln(eb - 1 )	e b > I	b = ln(e a + 1 )	I >- e a

Анализ таблицы 4 показывает, что при использовании подынтегральных функций f ( x ) = x ² и f ( x ) = x⁴ нет ограничений на выбор пределов интегрирования. В некоторых случаях ограничения могут быть не жесткими, например, для f ( x ) = 1/ x значения пределов интегрирования должны быть положительными числами. Ограничения могут быть и достаточно жесткими. Так для подынтегральной функции f ( x ) = x ³ генерация двух случайных чисел становится зависимой.

После генерации значения интеграла I верхний предел интегрирования должен генерироваться с учетом ограничения b ≥ ⁴ 4 ⋅ I .

Как известно [2], наиболее сложно произвести криптоанализ тех шифров, которые формируют равновероятную смесь чисел.

Для формирования шифрограммы с распределением чисел, близким к равномерному закону распределения, предлагается воспользоваться следующим алгоритмом.

Таблица 5.

Символы a1 a2 a3 an Частоты p1 p2 p3 pn gi =

pi pmin

В результате такого преобразования нормированные частоты будут лежать в пределах gi ≥ 1 . Величина gi показывает, во сколько раз частота появления данного символа больше, чем частота появления наиболее редко встречающегося символа в текстах, подвергнутых статистической обработке.

• 3.    Задается (выбирается) ширина интервала замен для символа с наименьшей частотой появления:

• 4.    Вычисляется ширина интервалов замен для остальных символов открытого текста

• 5.    Составляется таблица замен, в которой ширина интервала замен вычисляется по формуле (5), а положение интервала замен на числовой оси определяется сеансовым ключом. При этом все интервалы замен должны образовать непрерывную числовую последовательность. Границы интервалов замен будут, как правило, не целыми, а вещественными числами.

A ■ — d — с. min             .

A i = g i A min .                   (5)

Рассмотрим пример определения ширины интервала замен для каждого символа.

Таблица 6.

Буква	p i	Буква	p i	Буква	p i	Буква	p i
О	0.09	В	0.038	З	0.016	Ж	0.007
Е,Ё	0.072	Л	0.035	Ы	0.016	Ш	0.006
А	0.062	К	0.028	Б	0.014	Ю	0.006
И	0.062	М	0.026	Ь,Ъ	0.014	Ц	0.004
Н	0.053	Д	0.025	Г	0.013	Щ	0.003
Т	0.053	П	0.023	Ч	0.012	Э	0.003
С	0.045	У	0.021	Й	0.01	Ф	0.002
Р	0.04	Я	0.018	Х	0.009

Пусть частот таблица 6 задана:из нее видно,что этой буквы p _min = 0,002. После нормирования (вычис-реже всего встречается буква «Ф». Частота появления ление g _i = p _i / p _min )таблица 7 частот будет иметь вид

Таблица 7.

Буква	g i	Буква	g i	Буква	g i	Буква	g i
О	45	В	19	З	8	Ж	3,5
Е,Ё	36	Л	17,5	Ы	8	Ш	3
А	31	К	14	Б	7	Ю	3
И	31	М	13	Ь,Ъ	7	Ц	2
Н	26,5	Д	12,5	Г	6,5	Щ	1,5
Т	26,5	П	11,5	Ч	6	Э	1,5
С	22,5	У	10,5	Й	5	Ф	1
Р	20	Я	9	Х	4,5

Затем необходимо задать интервал замены для буквы «Ф». Выберем, например, A_min = 2. Далее вычисляется ширина интервалов замен для остальных символов открытого текста A i = 2 g i . В новом сеансе связи выбирается другое значение A min . Например, A min = 1,731 .

Дальнейшее усложнение рассмотренного алгоритма шифрования может быть осуществлено следующим образом. Найденная ширина интервала замен каждого символа дробится на n частей:

А,. = А,., + А;, + _ + А. .

i i1 i2 in

Затем все дробленые интервалы Δij всех символов тасуются (переставляются, перемешиваются) таким образом, чтобы образовать непрерывную числовую последовательность. Другими словами: каждой букве открытого текста ставится в соответствие не один, а несколько интервалов замен (как бы каждая буква равномерно распыляется по числовой оси).

Еще один прием дальнейшего увеличения криптостойкости заключается в том, что шифровку передают не парами чисел (которые соответствуют одному зашифрованному символу), а в разбивку: например, 4 верхних предела – 4 нижних; 3 верхних, 3 – нижних; 6 верхних, 6 – нижних и т.д. Порядок передачи верхних и нижних пределов определяется сеансовым ключом.

Вероятно, наиболее подходящими для шифрования будут подынтегральные периодические функции с изменяющейся амплитудой и частотой. Такие функции позволяют формировать на- иболее разнообразные значения интегралов на разных участках числовой оси.

Выводы

Предложен метод шифрования, основанный на замене символов открытого текста двумя вещественными числами. Одно из чисел генерируется с помощью датчика случайных чисел. Особенностью шифра является использование интегральных преобразований для получения второго числа. Другой особенностью описанного шифра является формирование таблицы замен, в которой символы распылены по числовой оси. Криптоанализ усложняется благодаря генерации двух случайных чисел (значения интеграла и одного из пределов). Секретный ключ определяет форму таблицы замен и вид подынтегральной функции.