Математические методы моделирования в эксперименте по оценке племенной ценности симментальских бычков

Автор: Мурленков Н.В., Лазарева Т.Н., Крюков В.И., Киреева О.С., Яркина М.В.

Журнал: Вестник аграрной науки @vestnikogau

Статья в выпуске: 1 (106), 2024 года.

Бесплатный доступ

Применение геномной селекции стало решающим научным скачком в эффективной реализации селекционных программ во всем мире. Размеры зарегистрированных популяций, применение современных технологий и одновременное тестирование большого количества маркеров на геноме животных привели к значительному прогрессу в области разведения скота по сравнению с традиционными методами селекции. В тоже время в качестве инструментов анализа необходимо оперировать современными методами, позволяющими выполнять все процедуры интеллектуальной обработки эмпирических данных. В представленной статье приведены результаты статистического анализа геномных индексов австрийских бычков с целью выявления ведущих информативных показателей. При обработке цифрового материала основной акцент делался на использовании приложения «SPSS Statistics» 27. Благодаря развитому аппарату статистического анализа программа позволила обработать большие массивы данных с высокой скоростью и точностью вычисления. Материалом для сравнительного анализа племенной ценности бычков служили следующие индексы: GZW - индекс общей племенной ценности; Mkg - индекс улучшения по молоку; F% - индекс улучшения по жиру; E% - индекс улучшения по белку; MW - индекс молочной продуктивности; FW - индекс мясных качеств; FIT - индекс, в совокупность которого входят геномные показатели (фертильность, SCC, долголетие). Представленные показатели позволяют дать сравнительную характеристику австрийских бычков симментальской породы в возрасте от 1 (n=211) до 2 (n=474) лет. Результаты исследования демонстрируют: наиболее сильные корреляции были получены при сравнении GZW с MW и Mkg - 0,631 и 0,531 (p function show_abstract() { $('#abstract1').hide(); $('#abstract2').show(); $('#abstract_expand').hide(); }

Еще

Симментальская порода, племенные индексы, продуктивность, бычки, (не) параметрические критерии, корреляционный анализ, факторный анализ

Короткий адрес: https://sciup.org/147244737

IDR: 147244737 | DOI: 10.17238/issn2587-666X.2024.1.38

Текст научной статьи Математические методы моделирования в эксперименте по оценке племенной ценности симментальских бычков

Введение. В работах отечественных и зарубежных авторов [2, 9, 13] актуальным направлением в селекции мясомолочного скота является разработка и использование новых методов оценки племенного потенциала животных. Поскольку фенотипический анализ не всегда дает объективную информацию о животном [11] (как правило, из-за наличия отрицательных корреляций между некоторыми линейными и молочными признаками), большую распространенность стал получать геномный способ оценки.

Геномная оценка является мощным инструментом в современной генетике, которая позволяет исследователям выявлять генетические маркеры, связанные с желаемыми характеристиками. Одним из ключевых методов, используемых в геномной оценке, является секвенирование ДНК [0] . Этот процесс позволяет анализировать последовательность нуклеотидов в геноме организма и выявлять различия, которые могут быть связаны с определенными фенотипическими характеристиками. В настоящий момент достоверность геномной оценки по продуктивным качествам составляет более 78%, что является эквивалентом 2550 дочерей в 20 стадах [8] .

George R. Wiggans [14] сообщает, что за последние годы геномная селекция удвоила скорость генетического прироста, прежде всего за счет сокращения интервала между поколениями (+6,6 млн в – 2022 г., на 5,5 млн больше, чем в 2021 г. (1,1 млн)).

В последние годы геномная оценка стала еще более эффективной благодаря включению новых показателей, например числа соматических клеток (SCC). SCC является мерой количества клеток, происходящих от неоднократных делений и мутаций в организме. Исследования показали [12], что высокое количество соматических клеток может быть связано с различными заболеваниями и повреждениями ДНК. Поэтому измерение SCC может быть полезным инструментом для оценки здоровья и возрастающего риска развития определенных заболеваний. Другой важный показатель, который включается в геномную оценку, – это долголетие. Изучение генетических маркеров, связанных с долголетием, позволяет исследователям лучше понять факторы, влияющие на продолжительность жизни. Это может быть полезно для разработки стратегий предотвращения возрастных заболеваний и повышения качества жизни животных [7]. Фертильность дочерей также стала важным показателем в геномной оценке. Исследования показали [9], что генетические маркеры, связанные с фертильностью, могут предсказывать способность животных производить потомство. Указанные показатели зарубежные ученые объединяют в индекс FIT (фитнес).

Однако наиболее важными признаками для отбора крупного рогатого скота все еще считаются продуктивность, качество семени, строение вымени, конечности, а также процентное содержание жира/белка в молоке. Для этих характеристик в животноводстве широко применяют обобщающие значения в виде средних, относительных величин и коэффициентов. К таким обобщающим показателям относятся и индексы. При всем многообразии селекционных индексов они представляют собой формулы сложения нескольких величин, отличающихся сочетанием одних и тех же компонентов, но в различном их соотношении между собой [5] . Таким образом, оценка наследуемости между признаками и индексами в геномном анализе позволит выявить наиболее подходящих особей для племенного дела.

В рассматриваемой статье основной упор делался на индекс GZW (Gesamt Zucht Wert), который широко используется в Германии, Австрии и Чехии для определения общей племенной ценности скота. Индекс GZW включает в себя 14 базовых значений, охватывающих молочную продуктивность, мясные качества и упомянутый выше фитнес. По мнению авторов [8] данный индекс помогает селекционерам достичь оптимальных результатов в разведении скота. Заводчики, занимающиеся разведением скота двойного направления продуктивности, делают упор на фитнес. В отличие от других стран, где акцент может быть сделан на молочности или экстерьерных показателях, немецкие селекционеры стремятся достичь баланса между продуктивностью и здоровьем скота. GZW является полифакторным (комплексным) индексом, который, помимо указанных значений, учитывает множество подфакторов, например белок и жир. При расчете GZW, селекционеры исключают экстерьерные показатели, чтобы уделять больше внимания фитнесу. Однако, в зависимости от изменяющихся требований и целей разведения, структура индекса GZW может меняться. Это позволяет адаптировать индекс к новым тенденциям и приоритетам в отрасли разведения скота.

Целью настоящей статьи являлась математическая оценка геномных индексов бычков мясомолочных пород австрийского происхождения. Для достижения поставленной цели осуществлялись следующие задачи: 1. определить и дать оценку нормальности распределения племенных индексов с помощью непараметрических и визуальных методов; 2. выявить взаимосвязь между племенными индексами бычков (корреляционный анализ); 3. обосновать влияние возраста на результативность улучшающих индексов (факторный анализ); 4. определить значимые различия между индексами бычков в зависимости от возраста (Критерий Стьюдента).

Материалы и методы исследований. Материалом для сравнительного анализа племенной ценности бычков служили следующие индексы: GZW – индекс общей племенной ценности; Mkg – индекс улучшения по молоку; F% – индекс улучшения по жиру; E% – индекс улучшения по белку; MW – индекс молочной продуктивности; FW – индекс мясных качеств; FIT – индекс, в совокупность которого входят геномные показатели (фертильность, SCC, долголетие). Представленные показатели позволяют дать сравнительную характеристику австрийских бычков симментальской породы в возрасте от 1 (n=211) до 2 (n=474) лет. Материальной основой для обработки индексов служили данные GGI-SPERMEX. Обработка племенных критериев осуществлялась в статистической программе «IBM SPSS Statistics» 27 при использовании (не) параметрических критериев.

Результаты исследований и их анализ. Уровень значимости является важным показателем в биометрии, особенно при проведении гипотезных тестов и принятии решений на основе статистических данных. Он позволяет определить, насколько результаты исследования или эксперимента статистически существенны. Поэтому перед применением параметрических методов, таких как корреляционный и факторный, необходимо удостовериться в соблюдении одного из ключевых условий – однородности исследуемой выборки и нормальности распределений показателей. Для проверки этого условия в данном случае мы использовали одновыборочный критерий Колмогорова-Смирнова (табл.1) и статистику Ливиня (табл. 2).

Таблица 1 – Одновыборочный критерий индексов бычков по Колмогорову-

Смирнову

Показатели	GZW \	MW \	FW \	FIT	Mkg \	F%	E%
1 год (n=211)
Статистика критерия	0,060	0,052	0,075	0,042	0,039	0,059	0,059
Асимп. знач.	0,065	0,200е	0,006	0,200е	0,200е	0,068	0,071
2 год (n=474)
Статистика критерия	0,092	0,085	0,058	0,060	0,055	0,054	0,047
Асимп. знач.	0,0001	0,0001	0,001	0,0001	0,002	0,002	0,012

Примечание: е – нижняя граница истинной значимости

Одним из методов для определения уровня значимости исследуемого критерия служил асимптотический показатель. Он используется при большом объеме данных с распределением, приближающимся к нормальному. Если показатель уровня значимости больше 0,05, мы можем считать выборку достаточно однородной. Полученные данные демонстрировали, что нормальность распределения индексов у бычков в возрасте 1-го года была характерна для GZW, MW, FIT, F%, E% – от 0,052 до 0,075 при асимптотической значимости от 0,065 до 0,2. Отметим, что показатель FW имел значимые различия на уровне 0,006, как и индексы бычков в возрасте 2-х лет – от 0,0001 до 0,012. Следовательно, для избегания неточностей при построении корреляционный матрицы желательно использовать данные за 1-й год.

При использовании дисперсионного анализа в программе SPSS, по умолчанию выполняется проверка однородности с применениеим критериев Фишера и Ливиня [6] . Критерий Фишера – это один из наиболее распространенных методов проверки однородности дисперсии. Он основан на сравнении отношения дисперсий между группами с ожидаемым отношением в случае, если дисперсии одинаковы. Однако, критерий Фишера не всегда обеспечивает точные результаты, особенно когда выборки имеют различные размеры или нарушены предположения о нормальности распределения (см. табл. 1). В отличие от критерия Фишера, критерий Ливиня является более точным методом проверки однородности дисперсии. Он основан на сравнении отношений дисперсий между группами с использованием аппроксимации хи -квадрата [3, 6] . Критерий Ливиня более устойчив к нарушениям предположений о нормальности распределения и различным размерам выборок. Если значение критерия Ливиня превышает уровень значимости 0,05, это свидетельствует об отсутствии статистически значимых различий в дисперсиях между группами.

Согласно данным таблицы 2, значимость критерия Ливиня однородной дисперсии для значений FIT, Mkg и E% составила 0,768, 0,069, 0,702 и статистически достоверно не отличалась на уровне 0,005. Следовательно, гипотеза не отклоняется, а применение дисперсионного анализа для данных показателей корректно. В случае с GZW, MW, FW, F% значимость меньше 0,05, гипотеза может быть отклонена, то есть дисперсии не равны.

Таблица 2 – Критерии однородности дисперсий исследуемых индексов

Показатель	Статистика Ливиня	ст.св.1	ст.св.2	знач.
GZW	4,815	1	683	0,029
MW	5,245	1	683	0,022
FW	4,255	1	682	0,040
FIT	0,087	1	683	0,768
Mkg	3,316	1	683	0,069
F%	5,028	1	683	0,025
E%	0,147	1	683	0,702

Примечание: ст.св. – степени свободы

Далее мы рассмотрим альтернативную оценку нормальности распределения показателей с помощью диаграмм. В литературе встречаются сведения [4] , что при больших объемах выборок (>50) целесообразнее использовать визуальную оценку нормальности распределения. На рисунках 1-3 представлены коробчатые диаграммы, которые для удобства просмотра были разбиты на подгруппы с большими и меньшими значениями. При анализе рисунков мы можем с уверенностью сказать, что выборка однородна: медианы всех семи показателей расположены практически посередине «ящичков», поэтому дальнейший анализ мы проводили с учетом визуализированного метода нормальности распределения индексов.

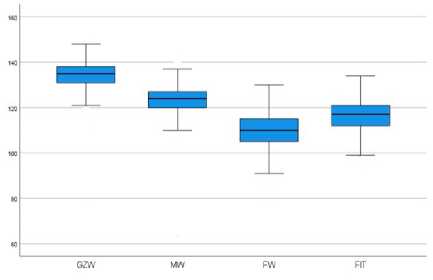
Рисунок 1 – Визуальная оценка индексов GZW, MW, FW и FIT на нормальность распределения

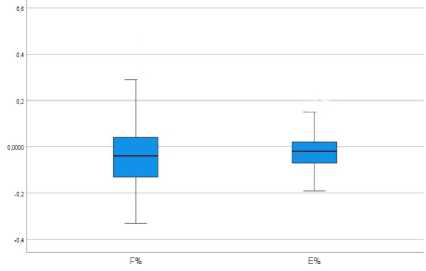
Рисунок 2 – Визуальная оценка индексов F% и E% на нормальность распределения

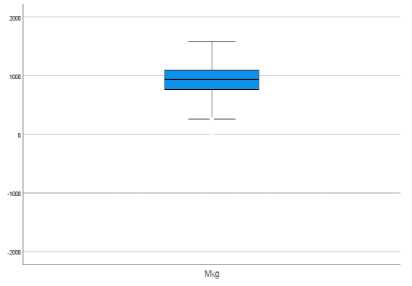
Рисунок 3 – Визуальная оценка индекса Mkg на нормальность распределения

На следующем этапе биометрических исследований мы выполнили корреляционный анализ с построением матрицы изучаемых индексов. Это позволило установить, влияние каких факторов является наиболее значительным.

Учитывая, что индекс GZW имел ранговое распределение, то, помимо классического коэффициента Пирсона, нами был также использован коэффициент Спирмена. Основное различие между двумя методами анализа заключалось в том, что коэффициент Пирсона применяется к линейной зависимости между переменными, тогда как коэффициент Спирмена работает с монотонными отношениями (где изменение одной переменной связано с изменением в определенном направлении другой переменной).

Согласно данным таблицы 3, наблюдалось, что часть выборочных коэффициентов парной корреляции, как Пирсона, так и Спирмена, статистически значима на уровне не меньше 0,0005. В частности подтверждается наличие связей между общим племенным индексом (GZW), молочной продуктивностью (MW, Mkg), качеством молока (F%, E%) и фитнесом (FIT). Так, согласно коэффициенту Пирсона, GZW сильно коррелируют с такими показателями как MW и Mkg – 0,631 и 0,531 (p<0,01) соответственно; индекс MW с Mkg – 0,631 (p<0,01); F% с E% – 0,647 (p<0,01); слабее, но также значима, была установлена связь между GZW и FIT – 0,423 (p<0,01). В противоположность этому процент жира (F%) и белка (E%) в молоке, с одной стороны, FW, с другой, имели либо слабую связь (GZW и FW – 0,369), либо не коррелировали с каким бы то ни было смежным показателем. Также отметим, что расхождение в значениях при оценке влияния факторов по коэффициенту Спирмена не имело критических отличий.

Таблица 3 – Корреляционная матрица индексов бычков

Показатели		GZW	MW	FW	FIT	Mkg	F%	E%
GZW	R Пирсона знач.	1	0,631^**	0,369^**	0,423^**	0,531^**	-0,053	-0,042
	R Пирсона знач.	-	0,0005	0,0005	0,0005	0,0005	0,169	0,267
	R Спирмена знач.	1,000	0,500^**	0,375^**	0,413^**	0,435^**	-0,053	-0,068
	R Спирмена знач.	-	0,0005	0,0005	0,0005	0,0005	0,170	0,076
MW	R Пирсона знач.	0,631^**	1	-0,030	-0,281^**	0,725^**	0,113^**	0,036
	R Пирсона знач.	0,0005	-	0,439	0,0005	0,0005	0,003	0,349
	R Спирмена знач.	0,500^**	1,000	-0,008	-0,348^**	0,646^**	0,148^**	0,033
	R Спирмена знач.	0,0005	-	0,844	00,0005	0,0005	0,0005	0,391
FW	R Пирсона знач.)	0,369^**	-0,030	1	-,069	0,029	-0,091^*	-0,031
	R Пирсона знач.)	0,0005	0,439	-	0,073	0,450	0,017	0,426
	R Спирмена знач.	0,375^**	-0,008	1,000	-0,106^**	0,054	-0,099^**	-0,038
	R Спирмена знач.	0,0005	0,844	-	0,006	0,155	0,009	0,316
FIT	R Пирсона знач.	0,423^**	-0,281^**	-0,069	1	-0,169^**	-0,107^**	-0,028
	R Пирсона знач.	0,0005	0,0005	0,073	-	0,0005	0,005	0,467
	R Спирмена знач.	0,413^**	-0,348^**	-0,106^**	1,000	-0,184^**	-0,104^**	-0,022
	R Спирмена знач.	0,0005	0,0005	0,006	-	0,0005	0,007	0,566
Mkg	R Пирсона знач.	0,531^**	0,725^**	0,029	-0,169^**	1	-0,559^**	-0,571^**
	R Пирсона знач.	0,0005	0,0005	0,450	0,0005	-	0,0005	0,0005
	R Спирмена знач.	0,435^**	0,646^**	0,054	-0,184^**	1,000	-0,559^**	-0,604^**
	R Спирмена знач.	0,0005	0,0005	0,155	0,0005	-	0,0005	0,0005
F%	R Пирсона знач.	-0,053	0,113^**	-0,091^*	-0,107^**	-0,559^**	1	0,647^**
	R Пирсона знач.	0,169	0,003	0,017	0,005	0,0005	-	0,0005
	R Спирмена знач.	-0,053	0,148^**	-0,099^**	-0,104^**	-0,559^**	1,000	0,622^**
	R Спирмена знач.	0,170	0,0005	0,009	0,007	0,0005	-	0,0005
E%	R Пирсона знач.	-0,042	0,036	-0,031	-0,028	-0,571^**	0,647^**	1
	R Пирсона знач.	0,267	0,349	0,426	0,467	0,0005	0,0005	-
	R Спирмена знач. (	-0,068	0,033	-0,038	-0,022	-0,604^**	0,622^**	1,000
	R Спирмена знач. (	0,076	0,391	0,316	0,566	0,0005	0,0005	-

Примечание: * – корреляция значима на уровне 0,05; ** – корреляция значима на уровне 0,01

Для выявления статистических различий из совокупностей анализируемых индексов был использован однофакторный дисперсионный анализ (Analysis of Variance, далее ANOVA). ANOVA является важным этапом статистического исследования, который позволяет выявить структуру исследуемых показателей, а также определить их связь с исходными значениями. Номинальным фактором, с которым проводили сравнение зависимых переменных, выступал возраст бычков – от 1-2 лет.

Поскольку размеры выборочных коэффициентов были идентичны числу измерений, возможность использования ANOVA является допустимым для всех показателей вне зависимости от нормальности распределения [10] .

Данные таблицы 4 наглядно демонстрируют влияние возраста на переменное значение индексов. Так, показатель критерия Фишера ( F ) для GZW, MW, FIT и Mkg составил 42,4; 24,9; 9,9 и 16,0 соответственно при уровне статистической значимости не хуже 0,0005. Для индексов FW, F%, E% критерий Фишера оказался незначимым, p-уровень для них составил 0,45; 0,39 и 0,03 соответственно, что позволяет принять нулевую гипотезу и сделать вывод об отсутствии различий у приведенных индексов.

Таблица 4 – Дисперсионный анализ селекционных индексов бычков

Показатели		∑ квадратов	ст.св.	Ср.квадрат	F	знач.
GZW	Между группами	1588,701	1	1588,701	42,442	0,0005
	Внутри групп	25566,531	683	37,433
	Всего	27155,232	684
MW	Между группами	962,239	1	962,239	24,910	0,0005
	Внутри групп	26383,854	683	38,629
	Всего	27346,093	684
FW	Между группами	25,521	1	25,521	0,453	0,501
	Внутри групп	38443,718	682	56,369
	Всего	38469,240	683
FIT	Между группами	508,358	1	508,358	9,947	0,002
	Внутри групп	34905,458	683	51,106
	Всего	35413,816	684
Mkg	Между группами	1323045,580	1	1323045,580	16,061	0,0005
	Внутри групп	56262174,794	683	82375,073
	Всего	57585220,374	684
F%	Между группами	0,001	1	0,001	0,039	0,843
	Внутри групп	11,427	683	0,017
	Всего	11,427	684
E%	Между группами	0,0005	1	0,0005	0,031	0,860
	Внутри групп	3,007	683	0,004
	Всего	3,007	684

Для определения критерия достоверности в первую очередь были рассчитаны значения средних, показатели рассеивания случайных величины (σ²) и среднеквадратичные ошибки ( MSE ).

Таблица 5 – Сравнение средних по изучению индексов бычков

Показатели	Возраст	N	Среднее	σ²	MSE
GZW	1 год	211	136,59	4,881	0,336
GZW	2 год	474	133,29	6,594	0,303
MW	1 год	211	125,21	4,940	0,340
MW	2 год	474	122,64	6,704	0,308
FW	1 год	211	110,39	6,982	0,481
FW	2 год	473	109,97	7,730	0,355
FIT	1 год	211	117,72	7,008	0,482
FIT	2 год	474	115,85	7,210	0,331
Mkg	1 год	211	991,73	243,138	16,738
Mkg	2 год	474	896,54	304,469	13,985
F%	1 год	211	-0,0340	0,14189	0,00977
F%	2 год	474	-0,0319	0,12337	0,00567
E%	1 год	211	-0,0221	0,06578	0,00453
E%	2 год	474	-0,0211	0,06660	0,00306

Примечание: σ² – среднеквадратичное отклонение; MSE – среднеквадратичная ошибка среднего

Обратим внимание, что среднее значения индексов F% и E% имело отрицательную динамку как за 1-й, так и за 2-й год: от -0,034 до -0,0319 и от -0,0221 до -0,0211 соответственно. Причем, при увеличении молочной продуктивности (Mkg) уровень жира (F%) в молоке снижался (таблица 5).

Эмпирические значения индексов (таблица 6) GZW, MW, FIT, Mkg по критерию достоверности (Tкр) равны 6,515, 4,991, 3,154, 4,008 при двусторонней значимости от 0,0005 до 0,002 (<0,005). Полученные результаты свидетельствуют, что между группами существуют различия, следовательно, нулевая гипотеза отвергается. Взаимосвязь между возрастом и FW была слабо выражена – на уровне 0,673 при значимости 0,501 (>0,005). Кроме того, индексы F%, E% имела обратную связь: -0,198 (знач. 0,843) и -0,176 (знач. 0,860) соответственно (>0,005). Можем предположить, что при достоверном увеличении количества надоев дочерей, одновременно происходило снижение качественного состава молока вне зависимости от возраста бычков.

Таблица 6 – Т -тест для независимых измерений индексов бычков

Показатели		T кр	ст.св.	знач.	Средняя разность	RMSE	95% интервал
Показатели		T кр	ст.св.	знач.	Средняя разность	RMSE	Нижняя	Верхняя
GZW	ПД	6,515	683	0,0005	3,299	0,506	2,304	4,293
GZW	НПД	7,292	533,455	0,0005	3,299	0,452	2,410	4,187
MW	ПД	4,991	683	0,0005	2,567	0,514	1,557	3,577
MW	НПД	5,596	535,639	0,0005	2,567	0,459	1,666	3,468
FW	ПД	0,673	682	0,501	0,418	0,622	-0,802	1,639
FW	НПД	0,700	443,446	0,485	0,418	0,598	-0,757	1,593
FIT	ПД	3,154	683	0,002	1,866	0,592	0,704	3,028
FIT	НПД	3,189	413,738	0,002	1,866	0,585	0,716	3,016
Mkg	ПД	4,008	683	0,0005	95,192	23,753	48,555	141,829
Mkg	НПД	4,364	497,812	0,0005	95,192	21,812	52,338	138,046
F%	ПД	-0,198	683	0,843	-0,00212	0,01070	-0,02314	0,01889
F%	НПД	-0,188	357,170	0,851	-0,00212	0,01129	-0,02433	0,02008
E%	ПД	-0,176	683	0,860	-0,00097	0,00549	-0,01175	0,00981
E%	НПД	-0,177	407,678	0,860	-0,00097	0,00546	-0,01171	0,00978

Примечание: ПД – предполагают равные дисперсии; НПД – не предполагают равные дисперсии; RMSE – среднеквадратичная ошибка разности.

Поскольку при изучении однородности выборки по критерию Ливиня у большинства индексов были выявлены значимые различия, нами дополнительно был рассчитан критерий Манна-Уитни для проверки достоверности.

Таблица 7 – Сводка U-критерия Манна-Уитни для индексов бычков

Показатели	GZW	MW	FW 1	FIT 1	Mkg	F% 1	E%
Всего				685
U Манна-Уитни	33053,5	36951,5	48892,0	43017,0	40143,5	51050,5	50704,5
Статистика критерия	33053,0	36951,5	48892,0	43017,0	40143,5	51050,5	50704,5
Стандартная ошибка	2386,7	2387,1	2384,5	2388,7	2391,1	2390,3	2388,5
Асимп. знач.	0,0005	0,0005	0,672	0,003	0,0005	0,662	0,770

Таблица 7 демонстрирует, что значимые различия между показателями были также выявлены по GZW, MW, FIT и Mkg – 33053, 36951, 43017, и 40143 при двусторонней асимптотической значимости от 0,0005 до 0,003 (<0,005) соответственно.

Выводы.

1. При оценке однородности и нормальности распределения показателей выборки, число измерений которой более 50, рекомендуем использовать визуальную оценку с помощью диаграмм.
2. Установлено, что наиболее сильные корреляции с общей племенной ценностью (GZW) были характеры для индексов молочной продуктивности (MW, Mkg) и фитнеса (FIT) – 0,631, 0,531 (p<0,01) и 0,423 (p<0,01) соответственно; взаимосвязь MW и Mkg также была значимой – 0,631 (p<0,01); процент жира (F%) и белка (E%) – 0,647 (p<0,01).
3. Критерий Фишера для общей племенной ценности (GZW), молочной продуктивности (MW, Mkg) и фитнеса (FIT) составил 42,4; 24,9; 16,0 и 9,9 соответственно при уровне статистической значимости не хуже 0,0005 – что свидетельствует о достоверном влиянии возраста на указанные индексы.
4. Достоверная значимость различий между индексами бычков за 1-2 годы наблюдалась по общей племенной ценности (GZW), молочной продуктивности

(MW, Mkg) и фитнесу (FIT) – 6,515, 4,991, 4,008, 3,154 на уровне от 0,0005 до 0,002 (<0,005).

Заключение. Согласно полученным результатам, к наиболее значимым индексам, влияющим на формирование общей племенной ценности, мы можем отнести молочную продуктивность и фитнесс. Логично будет предположить, что мясная продуктивность при оценке мясомолочного скота имела относительно слабое влияния на общую племенную ценность, поэтому данный индекс следует рассматривать отдельно. Изучение процентного содержания жира и белка в молоке выражало достаточно слабую взаимосвязь с молочными индексами. По нашему мнению это проявлялось из-за количественного увеличения продуктивных показателей при одновременном уменьшении качественных признаков.

Список литературы Математические методы моделирования в эксперименте по оценке племенной ценности симментальских бычков

Ахунов Э.Д., Вахитов В.А., Чемерис А.В. Секвенирование ДНК. М.: Наука, 1999. 429 с.
Карымсаков Т.Н., Абугалиев С.К., Баймуканов Д.А. Оценка племенной ценности быков-производителей по геномному анализу // Аграрная наука. 2019. № 10. С. 40-42.
Кричевец А.Н., Корнеев А.А., Рассказова Е.И. Основы статистики для психологов. - М.: Акрополь, 2019. 286 с.
Мастицкий С.Э., Шитиков В.К. Сатистический аналз и визуализация данных с помощью R . - М.: ДМК Пресс, 2015. 496 с.
Мельникова Е.Е. Построение селекционного индекса племенной ценности коров по признакам молочной продуктивности // Молочное и мясное скотоводство. 2016. № 8. С. 6-9.
Основы применения SPSS в социологии: Учеб. пособие / сост. А.К. Леонов. - Благовещенск: Амурский гос. ун-т, 2016 - 167 с.
Повышение продуктивного долголетия коров в условиях интенсивной технологии производства молока: научно-практические рекомендации / О. А. Быкова [и др.]. - Екатеринбург: Издательство Уральского ГАУ, 2020. - 92 с. 16
Позиционирование селекционера в странах Европы и Северной Америки [Электронный ресурс] / Режим доступа: https://ooobetagran.ru/wp-content/uploads/2022/09/Updated_СЕЛЕКЦИОНЕРУ-НА-ЗАМЕТКУ-для-КАТАЛОГА-08.2022-для-сайта.pdf (Дата обращения 20.07.2023).
Холодова Л.В., Смышляева А.А. Влияние геномной оценки быков-производителей на продуктивные качества их дочерей // Актуальные вопросы совершенствования технологии производства и переработки продукции сельского хозяйства. 2021. № 23. С. 507-509.
Chong G. Smoothing Spline ANOVA Models. - New York: Springer Series in Statistics, 2013. 452 p.
Gutiérrez-Reinoso M. A,. Aponte P. M., García-Herreros M. Genomic and Phenotypic Udder Evaluation for Dairy Cattle Selection: A Review // Animals 2023, Vol. 13 (10). pp. 2-24.
Seltsov V.I., Sermyagin A.A. Assessment of persistence components of milk from simmental cows-heifers of different origin // Russian Journal of Agricultural and Socio-Economic Sciences. 2014. Vol. 12 (36). pp. 3-8.
Single-step genomic evaluation of Russian dairy cattle using internal and external information / A. A. Kudinov [and etc.] // Journal of Animal Breeding and Genetics. 2022. Vol. 139 (3). pp. 205-270.
Wiggans G. R, Carrillo J.A Genomic selection in United States dairy cattle // Frontiers in Genetics 2022 [Электронный ресурс] / Режим доступа: https://pubmed.ncbi.nlm.nih.gov/36159997/ (Дата обращения 20.07.2023).

Еще

Статья научная