Математические модели динамических изображений на базе гиперкомплексных алгебр

Понятие изображения представляет собой сложный объект в силу ряда специфических информационных характеристик: информационной емкости, компактности, наглядности, внутренней структуры, отражающей логические и физические взаимосвязи окружающего мира, контекстной информации, статистических свойств и т.д. Такая сложность приводит к тому, что на сегодняшний день не существует единой точки зрения на теорию обработки и понимания изображений. Не имеется окончательной формулировки даже такого важнейшего первоначального понятия теории, как алгебра изображений [1–2].

На современном этапе для анализа изображений применяется огромное количество самых разнообразных по своей природе методов и подходов, среди которых не последнее место занимают эвристические и слабо проверенные методы, что неоднократно отмечалось рядом авторов, например работы [3–4]. В этой связи представляют интерес подходы, базирующиеся на строгих теоретических положениях, например, использующие аппарат теории сигналов, но применяющие упрощенные модели изображений объектов, не связанные со значительной потерей информации. Один из таких подходов заключается в отказе от обработки каждой точки изобра- жения и переходе к обработке лишь его контуров.

Контур целиком определяет форму изображения и содержит всю необходимую информацию для распознавания изображений по их формам. Методы контурного анализа в большей степени, чем растровые методы, дают возможность использовать модели, инвариантные к случайным переносам, поворотам и изменениям масштабов изображений. Исключительно важная роль анализа контуров подчеркивается в целом ряде оригинальных и обобщающих работ по распознаванию и обработке зрительных образов.

В этом плане интерес представляют монографии [5–6] авторского коллектива под руководством проф. Фурмана Я.А., полностью посвященные вопросам контурного анализа и его применений к обработке сигналов и изображений. В работе [5] преимущественно рассмотрены вопросы обработки и понимания плоских изображений на основе анализа комплекснозначных контуров и пучков векторов, а в работе [6] рассмотрены вопросы анализа 3D-изображений на основе кватернионных сигналов. Данная работа посвящена вопросам формирования аналитической модели контурного сигнала пространственного изображения динамического объекта, меняющего свои координаты в пространстве с течением времени.

Рис. 1. Пример сформированного бинарного изображения

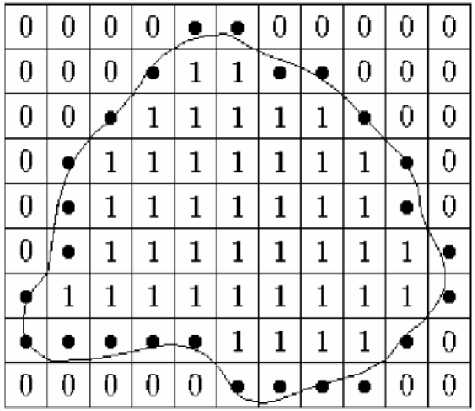
Рис.2. Задание точками граничных пикселей бинарного изображения при учете соседства только

по вертикали и горизонтали

Модели контуров изображений

Модели плоских изображений

Модель контура плоского изображения удобно представить на примере бинарного изображения, формируемого на этапе обнаружения, где пиксел, принадлежащий области изображения объекта, кодируется единицей, а пиксел, принадлежащий фону, кодируется нулем. На рис.1 представлен сформированный фрагмент бинарного изображения, а на рис.2 точками выделена соответствующая граница.

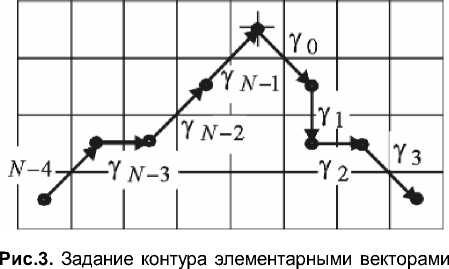
Для аналитического задания контура необходимо поставить в соответствие каждому граничному пикселю определенное число. Элементарный вектор (ЭВ) γ_n соединяет соседние граничные пиксели в направлении обхода; n - номер этого ЭВ, n = 0,1,..., к - 1, N – количество ЭВ в контуре данного изображения (рис.3).

Таким образом, произвольный контур Γ , состоящий из N ЭВ, задается в виде век- ординатами (xn; yn), а конец вектора в точке с координатами (xn+1; yn+1), то в комплекснозначном коде [5] ЭВ будет иметь вид:

Y n = ⁽ x n + 1 ^- x n ^{) +} i • ⁽ У п + 1 ^- У п ) . ⁽²⁾

Аналогичным образом можно получить аналитические модели плоских точечных изображений. На рис.4,а показана сцена, состоящая из N точечных объектов. Каждому точечному объекту соответствует один пиксел квадратной сетчатки оперативного запоминающего устройства. На рис.4,б точечные образы в сцене описываются цепочкой ЭВ, образующих контур г = {Zn }on—1, а на рис.1, в - пучком векторов B = {в }0 n-1.

Модели пространственных изображений

В работе [6] предложена модель в виде кватернионного сигнала для описания 3D- тора-столбца размерности N

^г = [ y о ; Y 1 ; Y 2 ;...; Y n - 1 ] T.         ⁽¹⁾

В дальнейшем для удобства записи выражение (1) будем представлять как ^Г = ^{ Y ^{( n )}} 0, N — 1 . Элементарные векторы яв-

ляются первыми разностями функций, задающих линию контура. Если начало n -го ЭВ контура изображения находится в точке с ко-

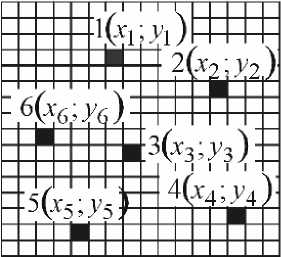
а)

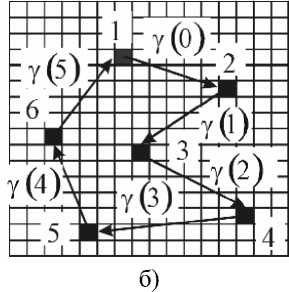
Рис.4. Формирование аналитического описания группового точечного объекта

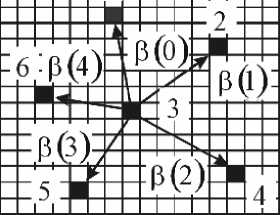
в)

изображений пространственных ГТО. Как и в случае плоских изображений, для аналитического описания пространственных изображений можно использовать как аналитическую модель кватернионного контура Γ , так и аналитическую модель пучка векторных кватернионов Q :

Г = ! Y ( n )}q,N-1 =

= { Y1 (n) i + Y2 (n) j + Y3 (n) k } ,

Q = { q ( n ) i o, N - 1 =

= { q i ( n ) • i + q 2 ( n ) • j + q 3 ( n ) • k } , ⁽³⁾ где n = 0,..., N - 1; Y i ( n ) , Y 2 ( n ) , Y 3 ( n ) , ( q i ( n ) , q 2 ( n ) , q 3 ( n ) ) - соответственно i -ая, j -ая, k -ая компоненты n -го элементарного вектора в составе кватернионного контура (пучка). На рис.5 показан пример представления кватернионного контура Γ и пучка векторных кватернионов Q .

Для математических моделей 3D-изоб-ражений точечных объектов достаточно лишь пучка векторных кватернионов Q (рис.5).

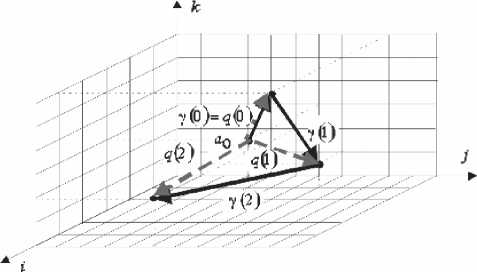
Рис. 5. Задание кватернионных контуров и пучков

Однако в результате ряда преобразований над такими сигналами элементарные векторы в составе кватернионных пучков могут представлять собой полный кватернион с неравной нулю реальной частью. Поэтому в общем случае для аналитической модели 3D-изоб-ражений точечных объектов будем использовать полные кватернионы. Следовательно, контур пространственного изображения можно рассматривать, как элемент линейного кватернионного пространства _H N .

Модели динамических пространственных изображений

Отметим, что рассмотренная выше математическая модель в виде пучка кватернионных ЭВ для описания 3 D -изображений пространственных ГТО использует информацию только о пространственных координатах точек X , Y , Z в декартовой системе к о ординат, где координате X соответствует i -ая компонента n -го ЭВ - q i ( n ) , координате Y соответствует j -ая компонента n -го ЭВ - q 2 ( n ) , а координате z соответствует k -ая компонента n -го ЭВ - q 3 ( n ) . Если положение каждой точки в пространстве-времени рассматривать, как некоторый вектор с координатами:

5 = c • t + X • x + Y • y + Z • z, (4) где c - скорость света, t - время, X , Y , Z -координаты точки в трехмерном пространстве в декартовой системе координат; то получим математическую модель 3D-изображе-ния динамического пространственного изображения ГТО. При этом изображение форми- руется при смене двух последовательных кадров в течение некоторого наблюдаемого интервала времени t = ti -tо. В момент времени t0 формируется аналитическое описание пространственного ГТО, представленного пучком векторов O = {o(n)}о n-1. В момент времени t1 формируется аналитическое описание пространственного ГТО, представленного сигнальным пучком векторов O(c) = o(c)(n)}о n—i. Причем за время t между двумя кадрами изображений пространственный ГТО перемещается вдоль оси p с некоторой постоянной скоростью ϑ, и поворачивается вокруг оси p на угол ϕ (рис.6).

В работе [7] показано, что

• 5 ² = ( ct ) ² - X ² - Y ² - Z 2.       (5)

• - квадратичная форма специальной теории относительности, ассоциированная с алгеброй пространства-времени. Для рассмотрения алгебры пространства-времени выберем алгебру комплексных матриц специального вида, изоморфную алгебре бикватернионов [8].

Бикватернионы представляют собой систему гиперкомплексных чисел, состоящую из восьми компонент с базисными элементами 1, i , j , k , d , E , I , J , K . Произвольный бикватернион можно представить в виде:

o = a + b • i + c • j + d • k + A • E + B • I + C • J + D • K . (6) Сложение и умножение двух бикватернионов производится покомпонентно. Умно-

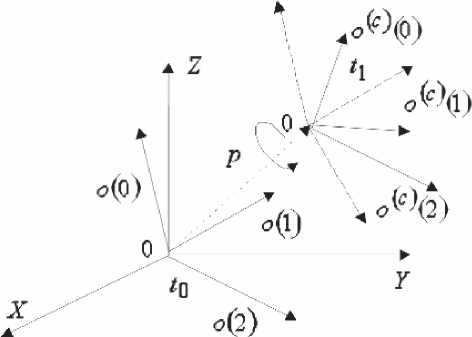
Рис.6. Аналитическая модель динамического 3D-изображения группового точечного объекта жение бикватернионов полностью определяется таблицей умножения базисных элементов. Таблица умножения базисных элементов бикватернионов имеет вид:

X	1	i	j	k	E	I	J	K
1	1	i	j	k	E	I	J	K
i	i	- 1	k	- j	I	- E	K	- J
j	j	- k	- 1	i	J	- K	- E	I
k	k	j	- i	- 1	K	J	- 1	- E (7)
E	E	I	J	K	- 1	- i	- j	- k i
I	I	- E	K	- J	- i	1	- k	j
J	J	- K	- E	I	- j	k	1	- i
K	K	J	- 1	- E	- k	- j	i	1

Бикватернионы обладают следующими свойствами: коммутативны по сложению, и не коммутативны по умножению; ассоциативны по сложению и по умножению; дистрибутивны.

Из выражения (6) следует, что бикватернион состоит из двух кватернионов:

o = q + E • q ' = ( a + bi + cj + dk ) + E ( A + Bi + Cj + Dk ) , (8) где E - мнимая единица удвоения кватернионов. Такое представление бикватерниона всегда возможно, и оно единственно. Произведение двух бикватернионов o ( 1 ) = q ( 1 ) + Eq ' ( 1 ) , o ( 2 ) = q ( 2 ) + Eq ' ( 2 ) , с учетом записи (8), можно рассматривать следующим образом:

o ( 1 ) • o ( 2 ) = ( q ( 1 ) + Eq ' ( 1 )) • ( q ( 2 ) + Eq '( 2 )) = (9) = ( q ( 1 ) • q ( 2 ) - q ' ( 1 ) ^ q ' ( 2 )) + E ( q ' ( 1 ) ^ q ( 2 ) + q ( 1 ) ^ q ' ( 2 )) , где произведения q ( 1 ) ^ q ( 2 ) , q ' ( 1 ) ^ q ' ( 2 ) , q ' ( 1 ) • q ( 2 ) , q ( 1 ) • q ' ( 2 ) выполняются в соответствии с правилами умножения кватернионов.

Сопряжение бикватерниона образуется сменой знаков у компонент, в образовании мнимых единиц которых участвовали мнимые единицы:

o = a - b • i - c • j - d • k - A • E - B • I - C • J - D • K .(10)

Скалярная часть бикватерниона:

o скал = a + A • E .          (11)

Векторная часть бикватерниона (бивектор):

o ^век = b • i + c • j + d • k + B • I + C • J + D • K . (12)

Любой бикватернион можно представить в виде суммы скалярной и векторной частей:

скал век o = o + o .

Определим правый обратный бикватер- нион o 1 = Q + eq' такой, что oo-1 = (q + Eq ')(Q + EQ ') = 1 - (14)

Из выражения (9) следует, что для нахождения правого обратного бикватерниона требуется выполнение двух равенств:

<

' qQ — q' Q' = 1, _ q ' Q + qQ ' = 0.

Тогда параметры обратного бикватерниона имеют вид:

Q = ( q + q ' q ¹ q ' ) , Q ' = - q ¹ q ' Qnpu q * 0;

Q = 0, Q ' = - ( q ' )^{- 1}              и q = 0, q ' * 0.

(15) где q ^{- 1} - обратный кватернион; q ' q ^{- 1} q ', q ^{- 1} q ' Q - произведения кватернионов.

Обратный кватернион (q + q‘q-1 q‘) 1 существует в том и только в том случае, когда q + q' q-1 q' * 0- (16)

В случае не выполнения условия (16) обратного правого бикватерниона не существует. Определим общий вид бикватерниона o , не имеющего правого обратного. Для этого требуется решить уравнение вида:

q + q ' q ^{- 1} q ' = 0 - ⁽¹⁷⁾

Таким образом, из уравнения (17) следует, что бикватернионы, не имеющие правого обратного, можно получить из произвольного бикватерниона o = q + Eq ' с q * 0 , используя

oноль =(4 + Eq% + B ■ I + C■ J + D■ K),(18)

oноль ■ o*оль = 0- скал 2 век 2     ,

\oноль/   oноль/ причем, бикватернион - делитель нуля oноль представляет собой нильпотенту если

(o ноль)2 = 0, а бикватернион – делитель нуля oноль представляет собой идемпотенту если скал 2     .

\oноль / * vv 7

Матричная интерпретация бикватернионов

Бикватернионы вида (6) можно задать квадратной комплексной матрицей четвертого порядка:

a - d ■ i - c - b ■ i D + A ■ i B - C ■ i c - b ■ i a + d ■ i B + C ■ i - D + A ■ i

O =

D + A ■ i B - C ■ i a - d ■ i - c - b ■ i -

_ B + C ■ i - D + A ■ i c - b ■ i a + d ■ i

Матрицы E , I , J , K , E ', I ', J ', K ' , соответствующие базисным элементам

• 1, i ,    j , k , E , I , J , K бикватерниона, выразим из базисных матриц четырехмерного векторного пространства-времени T , X , Y , Z :

	" 1	0	0	0 "		" 0	0	0	- 1 "
	0	1	0	0		0	0	- 1	0
T =	0	0	- 1	0	, X =	0	1	0	0	,
	_ 0	0	0	- 1 .		. 1	0	0	0 .
	" 0	0	0	i		" 0	0	- 1	0 "
	0	0	- i	0		0	0	0	1
Y =	0	- i	0	0	, Z =	1	0	0	0	. (24)
	. i	0	0	0 .		. 0	- 1	0	0 .

В результате получим:

^где B ² + C ² + D ² = 1-

Бикватернионы, не имеющие правого обратного, обладают следующими свойствами:

"0 0 i 0" " ct 0 -Z - X + Y • i" 0 0 0 i 0 ct - X - Y • i Z E' = T • X • Y • Z = i 0 0 0 ,     (25) Z X - Y • i - ct 0 ,(26) X + Y • i - Z 0 - ct [0 i 0 0] L -J где матрицы T , X , Y , Z - базисные матри-

I = Y • Z =

J = Z • X =

- i

K = X • Y =

J ' = Z • T =

K ' = X • T =

- i

- i

- i

- 1

- 1

- i 0 0 0

0 i 00

0 0 - i 0

000 i

I ' = X • T =

0	0	0	1
0	0	1	0
0	1	0	0
1	0	0	0

0 0 0 - i

00 i 0

0 - i 0 0

i 000

- 1 0

- 1

В матричных обозначениях вектор пространства-времени определится как:

S = (ct) • T + X • X + Y • Y + Z • Z =

цы четырехмерного векторного пространства, определенные в соответствии с выражением (24).

Преобразование вида

S ' = R • S • R ^{- 1} , ⁽²⁷⁾

является лоренцовым вращением пространства-времени. Здесь R - такой бикватернион в матричных обозначениях, что R • R ^{- 1} = E , R ^{- 1} — обратный бикватернион.

Далее запишем выражение для бикватернионов r и r ^{- 1}. Сгруппируем слагаемые в составе матричного представления бикватерниона (23), выделив векторную часть:

B = b • I + c • J + d • K + B • I ' + C • J ' + D • K ' =

= -[( b • I + c • J + d • K )• E ']• E'+

+ ( B • I ' + C • J ' + D • K ' ) = о • E ' + о ' , (28) где σ и σ ' - векторы пространства:

	"     0	0	- d	- b + c • i "
° =	0	0	- b - c • i	d	, (29)
	- d	- b + c • i	0	0
	_- b - c • i	d	0	0    ]

	"     0	0	D	B - C • i "
	0	0	B + C • i	- D
о ' =					. (30)
	D	B - C • i	0	0
	_ B + C • i	- D	0	]

В результате для бикватерниона R в матричных обозначениях каноническое разложение будет иметь вид:

R = ( ch (0/ 2 ) - E + B • sh (6/ 2 ) ) x

x ( cos ( ^ 2 ) • E + E ' • B • sin ( ^ 2 ) ) ,

R ¹ = ( ch ( 0 / 2 ) • E - sh ( 0 / 2 ) • B ) x

x ( cos ( ^ 2 ) • E - sin ( ф /2 ) • E ' • B ) . (31)

Лоренцовое вращение пространства-времени (27) можно интерпретировать как:

• 1)    Вращение в трехмерном пространстве. К ним приходим в случае

о = 0, B = - A - I ' - B - J ' - C - K ',

A ² + B ² + C ² = 1.      ⁽³²⁾

Тогда вращающий бикватернион R и обратный к нему бикватернион r — 1 представляют собой кватернионы и имеют следующий вид:

R = cos (ф( 2 ) - E + sin (ф/ 2 ) - ( A - I + B - J + C - K ) R ^{- 1} = cos ( ф 2 ) - E - sin ( ф 2 ) - ( A - I + B - J + C - K ) ,(33) ϕ - угол поворота вокруг оси p , с координатами x = A , y = B , z = C .

Получаем обычные вращения в трехмерном пространстве.

• 2)    Специальные преобразования Лоренца. К ним приходим в случае

Ф = 0, B = C - K ', A = 0, B = 0, C = 1. (34)

Тогда вращающий бикватернион R и обратный к нему бикватернион r ^{- 1} в матричных обозначениях будут иметь вид:

R = ch I ⁰ |- E + sh I ⁰ |- K '

1 2 J 1 2 J ,

R ^{- 1} = ch | ⁰ |- E - sh | ⁰ |- K '

i 2 J I 2 J . ⁽^^ )

Если исходное положение точки в пространстве-времени задавать некоторым вектором 5 = c - t + X - x + Y - y + Z - z , то в результате специальных преобразований Лоренца новое положение точки будет задаваться вектором 5 ' = ( c - t ' + X ' - x + Y ' - y + Z ' - z ) , где:

X ' = X ,

Y ' = Y ,

Z ' = Z - ch ( 0 ) - c - t - sh ( 0 ) ,    (36)

c - t ' = c - t ' - ch ( 0 ) - Z - sh ( 0 ) .

Перепишем два последних равенства выражения (36) в виде:

' Z ' = ch ( 0 ) - ( Z - c - t - th ( 0 ) ) ,

\ t ' = ch ( 0 ) - ( t - ( Z/c ) th ( 0 ) ) .     ⁽³⁷⁾

Выражение (37) представляет собой специальное преобразование Лоренца-Эйнштейна. При фиксированном параметре θ из выражений (36) и (37) следует, что если Z = c - 1 - th ( 0 ) , X = Y = 0 , то X ' = Y ' = z ' = 0 .

Это показывает, что преобразование состоит в равномерном и прямолинейном сдвиге выделенных координатных осей вдоль направления противоположного направлению оси OZ . При таком подходе, если обозначить ϑ th 0 )= c,            (38)

вытекает условие, что скорость движения ϑ не может быть больше скорости света c .

• 3) . Прямолинейное равноускоренное движение точки с вращением вокруг оси, задаваемой направлением движения (винтовое движение).

Рассмотрим вращающий бикватернион в случае, когда задающий его бивектор имеет следующий вид:

B = B - 1 ' + C - J ' + D - K ' ,

B ² + C ² + D ² = 1 .         ⁽³⁹⁾

где B , C , D - задают координаты оси p вдоль которой происходит движение и вращение точки. Тогда вращающий и обратный к нему бикватернионы имеют следующий вид:

R = [ch (02)- E + sh (02)-(B -1'+ C - J'+ D - K ')]x x |^cos (ф/2) - E + sin (ф/2) - (B -1 + C - J + D - K)] =

= ch ( 0 2 ) - cos ( ф 2 ) - E +

+ ch ( 0 2 ) - sin ( ф 2 ) - ( B - 1 + C - J + D - K ) +

+ sh ( 0 2 ) - cos ( ф 2 ) - ( B - 1 ' + C - J ' + D - K ' ) -

• -    sh ( 0 2 ) - sin ( ф 2 ) - E ' ,

R ^{- 1} = ch ( 0 2 ) - cos ( ф 2 ) - E -

- ch ( 0 2 ) - sin ( ф 2 ) - ( B - 1 + C - J + D - K ) -

- sh ( 0 2 ) - cos ( ф 2 ) - ( B - 1 ' + C - J ' + D - K ' ) -

• -    sh ( 0 2 ) - sin ( ф 2 ) - E ' .        (40)

Рассмотренные выше виды преобразований пространства-времени: вращение, специальные преобразования Лоренца и винтовое движение можно выполнять и в виде про- изведения бикватернионов вида:

o ⁽ c ) = r - o - r ,                   ⁽⁴¹⁾

где r - вращающий бикватернион r = cos ( ф/2 ) - ch ( 0/2 ) +

+ sin (ф/2) - ch(0/2) -(B - i + C - j + D - k )-

• -    sh ( 0/ 2 ) - sin ( ф/2 ) - E +

+ cos (ф/ 2 ) - sh (0/ 2 ) - ( B - 1 + C - J + D - K ) , (42) ^~ _r - “сопряженный” бикватернион к бикватерниону r по следующему правилу:

r = cos ( ф/ 2 ) - ch ( 0/ 2 )

• - sin(ф/2) - ch(0/2) -(B - i + C - j + D - k) +

+ sh (0/ 2)- sin (ф/2)- E +

+ cos (ф/ 2 ) - sh (0/ 2 ) - ( B - 1 + C - J + D - K ) , (43) o - бикватернион, соответствующий исходному вектору пространства-времени

S = c -1 + X - x + Y - y + Z - z o = [c -1 0 0 0 0 X Y Z ], (44) o(c) - бикватернион, соответствующий полученному в результате лоренцового вращения вектору пространства времени

S ' = c - 1 ' + X ' - x + Y ' - y + Z ' - z

o ^{( c} ) = [ c - 1 ' 0 0 0 0 X ' Y ' Z ' ] , (45) B , C и D - координаты оси вращения – движения, такие , что в ² + C ² + D ² = 1 •

Отличие представления лоренцового вращения пространства-времени в виде (41) от матричного (27) заключается в том, что в выражении (41) вместо обратного бикватерниона r - 1 , как это было в матричном представлении ( r - 1 ), используется “сопряженный” бикватернион (43). Это связано с тем, что представление вектора пространства-времени в матричном виде, отличается от матричного представления вектора пространства.

Пространства бикватернионных сигналов

Рассмотрим два бикватернионных сигнала O = {о(n )}0, n-1 и U = {u(n )}0, n-1, где каждый бикватернионный ЭВ в общем виде соответствует выражению (6). Бикватернион-ный сигнал можно рассматривать как элемент N -мерного линейного пространства ON . Произведение и сложение бикватернионных сигналов выполняется поэлементно. В результате сложения или умножения полных бикватернионных сигналов образуется новый бикватернионный сигнал. Бикватернионный сигнал обладает структурой ассоциативного кольца. В силу того, что операция умножения над кольцом бикватернионов O является некоммутативной, будем различать правое O N линейное пространство бикватернион-ных сигналов, в котором умножение биква-тернионного сигнала O = {o(n )}0, n-1 на скаляр o (при о е on , o е O), удовлетворяет следующим аксиомам:

• ^а)    O - o е O N ,

• б)    ( O + U ) - o = O - 0 + U - o ,

• в)    O - ( o 1 + o 2 ) = O - o 1 + O - o 2 ,

• г)    O - (o - o) = (O - o)- o,

• д)    о - 1 = о •

Скалярное произведение в пространстве _O ^N при ортонормированном базисе имеет вид:

N - 1

^{( о} , ^U ) = Z ^{o (} n ^{) -V} n •         (46)

n = 0

Евклидовую норму произвольного биква-тернионного сигнала O можно выразить, используя свойство скалярного произведения:

II 011 = 7( 0 , 0 )

N - 1 7

XX ol (n )2

n = 0 l = 0

Для любых двух бикватернионных сигналов O и U справедливо неравенство Коши-Буняковского:

I ( O , U ) ²<| |O|| ²-I |U|| ².           ⁽⁴ 8)

Нормированное скалярное произведение зададим выражением:

cos ф =

( O , U )

II 011 -||U|I.

В рассматриваемом евклидовом биква- тернионном пространстве ON со скалярным произведением контуров пространственновременных изображений (46) введем расстояние между двумя бикватернионными сигналами:

R = |O - U| .           (50)

Используя выражение (50) можно записать:

R ² = O - U| ² = ( O - U , O - U ) =

=ЮН2 +1 U 12-(O. U )-(U. O)

Введенное представление удовлетворяет следующим условиям:

R O , O = ^{0 ,} R O , U = R U , O .

Евклидовое бикватернионное пространство N -ой размерности является полным.

Спектральный анализ бикватернионных сигналов

В работе [9] для спектрального и корреляционного анализа кватернионных сигналов предлагается использовать базисные функции неприводимых представлений ортогональной группы O(3), которые представляют собой сферические гармоники. Для спектрального анализа бикватернионных сигналов можно также использовать базисные функции неприводимых представлений ортогональной группы O(d). При использовании процедуры удвоения для формирования гиперкомплексной системы получим, что размерность пространства d - кратна степени 2 (для бикватернионов d = 23 = 8 ). При этом полярный вектор в гиперкомплексном пространстве, кроме d = 2, всегда содержит нечетное количество координат, так как нулевая компонента ЭВ - представляет собой скаляр, не имеющий отношения к пространственным координатам полярного вектора. Рассмотрим неприводимые представления ортогональной группы O(d) только для не четных d < 8.

Правило построения неприводимых представлений ортогональной группы O ( d ) имеет следующий вид: все допустимые схемы для заданного значения d определяются, полагая r = 0,1,2,... и отбирая неотрицательные числа ц , удовлетворяющие уравнению:

Ц 1 + ц 2 + ... + Ц у = r ,        (52)

где Ц 1 > ц 2 >  ... > ц_v , причем некоторые из чисел Ц могут быть нулями; d = 2 _v , если d четно, и d = 2 _v + 1, если d нечетно.

При d = 3 : _v = 1. Поэтому неприводимые представления группы о ⁺( з ) описываются одним значком Ц 1 . Базисными функциями служат симметрические тензоры щ-го ранга с нулевым следом.

При d = 5: _v = 2. Следовательно, неприводимые представления группы о ⁺ ( 5 ) характеризуются двумя целыми числами (щ ц 2 ) , причем Ц 1 > ц 2 .

При d = 7 : _v = 3 . Следовательно, неприводимые представления группы о + ( 7 ) характеризуются двумя целыми числами ⁽Ц 1 Ц 2 Ц 3 ) ^, причем Ц 1 >Ц 2 >Ц 3 .

Работа выполнена при финансовой поддержке гранта РФФИ №04-01-00243.