Математические модели динамики эпидемий и их исследование

Современная эпидемическая ситуация привлекла всеобщее внимание к проблемам возникновения, распространения и развития таких процессов. Существует множество исследований, посвященных распространению как привычного сезонного гриппа, так и опасных эпидемических заболеваний [12].

Всемирная организация здравоохранения располагает банком данных, содержащих количественную информации о динамике таких процессов как в отдельных странах, так и по миру в целом [14].

4 в ыпуск 3/2020

Авторы считали своей задачей провести анализ основных количественных закономерностей таких процессов на основе методов построения математических моделей по эмпирическим данным [4; 5; 6; 7; 8; 10].

Единственный эффективный способ определить принадлежность результатов измерений к анализируемой модели, оценить ее параметры состоит во введении такой системы преобразований исходных данных, которая переводит их в линейную зависимость. Как известно, такие преобразования называются анаморфозами. В результате по официальным данным о динамике эпидемических заболеваний на основе тестирования систем анаморфоз определялись конкретные виды математических моделей, соответствующих реальным результатам измерений.

При этом имелось в виду, что эпидемии представляют собой сложный нелинейный процесс, состоящий из иерархии стадий, идущих в разных характерных временах, что требует решения задачи о разделении движений, соответствующих механизмам, реализуемым на разных структурных уровнях. Принципиальным для этих процессов является также существенное влияние на их развитие инкубационного периода заболевания.

Следующая принципиальная особенность этих процессов состоит в реализации последовательности естественных стадий процесса, принципиально зависящих как от типологии вируса, так и от иммунитета популяции, организации здравоохранения, противоэпидемических мероприятий, природно-климатических условий. Естественные параметры таких стадий представлены числом тестов, общим и ежедневным числом зараженных и смертностью.

Наибольший интерес был уделен динамике коронавируса. На основе анализа динамики распространения этой эпидемии из многих десятков стран мира были отобраны для представления в данной статье Италия как наиболее пострадавшая страна в Европе, США как лидер по числу заболевших и данные по миру в целом.

Общие характеристики эпидемических процессов

В принципе общая структура таких процессов, по данным о еженедельном числе смертельных случаев от пневмонии в США [14], представлена на рисунке 1.

Данные рисунка 1 наглядно показывают периодический характер этого процесса с естественным периодом, равным одному году, что обращает внимание на значимость сезонных колебаний температуры. Данные рисунка 1 показывают, что для годичного цикла это процесс ограниченного роста.

При этом общее количество случаев для каждого из этих годичных циклов представлено на рисунке 2. На рисунке 2 унимодальная кривая значимо представлена последовательностью двенадцатилетних равномерных интервалов. В то же время каждой точке соответствует годичная кривая ограниченного роста. Такая структура эпидемических процессов является общей – число заболевших за единицу времени растет, достигает максимума и затем убывает, а общее число заболевших характеризуется кривой ограниченного роста.

Примером таких характеристик эпидемических процессов являются данные, приведенные на рисунке 3.

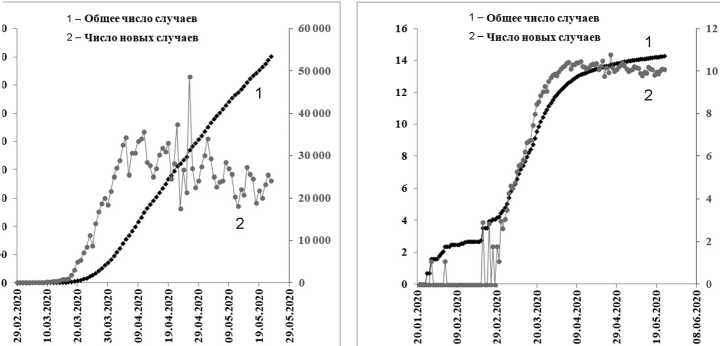
Рассмотрим реальную динамику заболеваемости коронавирусом в Италии по данным [8] (рис. 4). Бóльшая часть данных недоступна для анализа в связи с большим диапазоном изменения значений по ординате. Для обеспечения возможности анализа данных во всем диапазоне требуется перейти к логарифмическому масштабу для числа заболевших.

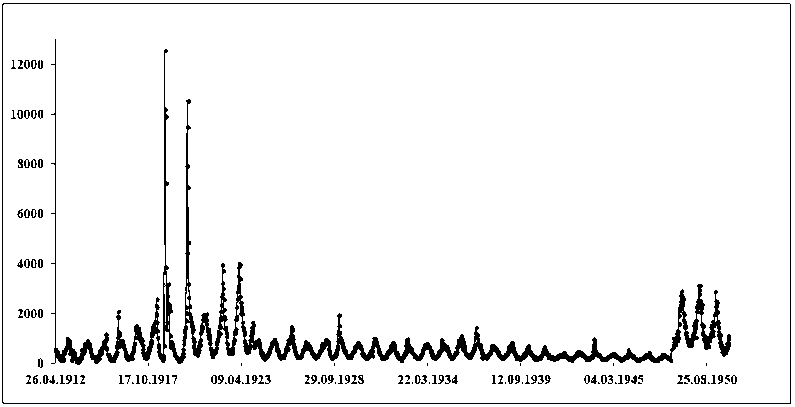
Рис. 1. Еженедельное число смертельных случаев в США от пневмонии с 1912 по 1950 г.

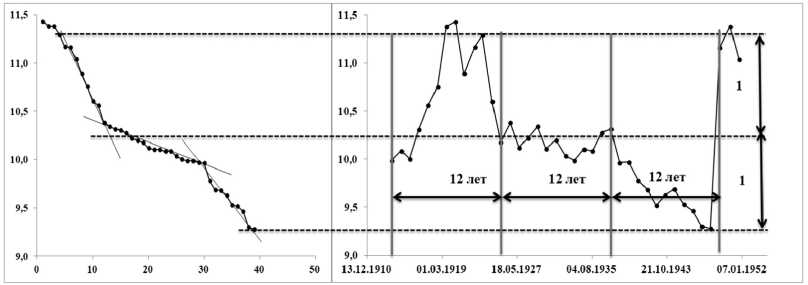
Рис. 2. Натуральный логарифм количества смертельных случаев на каждом из годичных циклов (справа) и соответствующее ему ранговое распределение (слева)

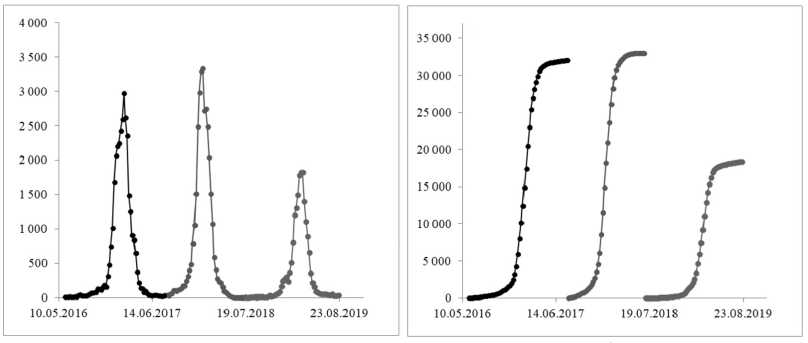
Рис. 3. Динамика новых случаев эпидемии АН1 в США: а – число заболевших за единицу времени; б – общее число заболевших

Выпуск 3/2020

а                                              б

Рис. 4. Динамика заболеваемости коронавирусом в Италии: а – линейный масштаб; б – логарифмический масштаб

Аналогичные данные для США представлены на рисунке 5- а , те же данные на рисунке 5- б – в полулогарифмическом масштабе, что позволяет детализировать начальный участок процесса.

1000 000

800 000

600 000

400 000

1 SOO ООО

1 600 000

1400 000

б

а

Рис. 5. Динамика заболеваемости коронавирусом в США: а – линейный масштаб; б – логарифмический масштаб

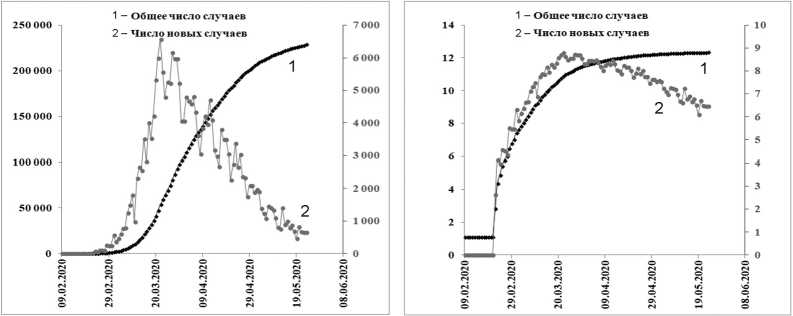
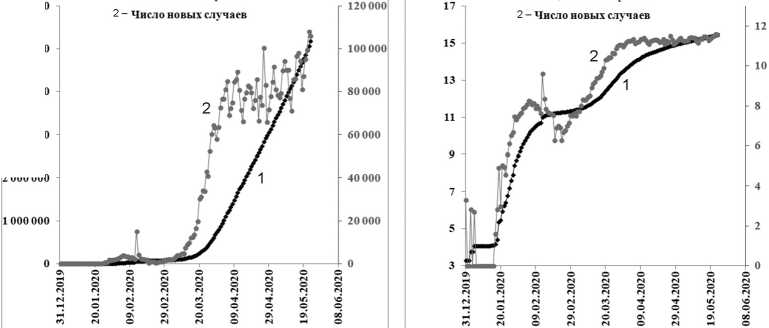
Более сложной динамикой отличаются мировые данные по заболеваемости (рис. 6). Построение в таких координатах позволяет выявлять последовательность стадий развития процесса на уровне мировой эпидемии. Здесь очевидна реализация периода индукции, стадии с небольшим количеством вовлеченных в процесс людей и переходом к следующей стадии, когда была реализована мировая эпидемия.

Такие процессы широко распространены в природе и технологиях, и их характеристики наиболее часто анализируются на основе модели Гомперца [11] и логистической модели [9].

Гадзаов А.Ф., Кузьмин В.И., Самохина А.С. Математические модели динамики...

1 - Общее число случаев

6 000 000

5 000 000

4 000 000

3 000 000

1 - Общее число случаев

2 000 000

б

а

Рис. 6. Динамика заболеваемости коронавирусом в мире: а – линейный масштаб; б – логарифмический масштаб

Использование анаморфоз для применения модели Гомперца и логистической модели при анализе динамики эпидемий

Основой этих моделей является зависимость темпа ее роста от времени либо размера системы. Темпом называется отношение скорости роста системы к ее размеру:

^

- = f ⁽ t > У )                                  ⁽¹⁾

y

Модель Гомперца. При f (t,у) = Aexp(—kt) получим модель Гомперца, которую он ввел для оценки рисков при страховании, т.е. речь идет о прогнозировании той же смертности. Для модели Гомперца dy = Ae " kty.                                   (2)

dt

Из исходного уравнения модели Гомперца (2) получается анаморфоза ln —У- = ln( A ) — kt. I у dt J

Построение данных, соответствующих модели Гомперца, дает спрямление в коорди-

1 dy натах ln —— <  У dt

~ t. Это задает алгоритм определения параметров уравнения (2), как это показано на рисунке 5. В этом случае по линейному участку зависимости находим параметр k, который определяется углом наклона прямой к оси абсцисс (рис. 7).

d ² у

Уравнение Гомперца имеет точку перегиба, в которой   2- = 0. Тогда из исходного уравнения (2) имеем                                   dt

• d У        — kt       — kt ^dy ^dy    — kt

• —= — Ake у + Ae — = Ae — k = 0 .

dt2           7 dt dt откуда во временной точке максимума скорости t0

или

Выпуск 3/2020

Ae

- kt 0

[

1 dy' y dt ,

^(t o ) = k ,

ln 1 dy

[ ydt)

= ln k .

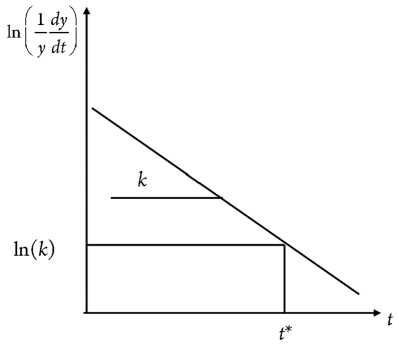
Рис. 7. Определение времени достижения точки перегиба по значению параметра k

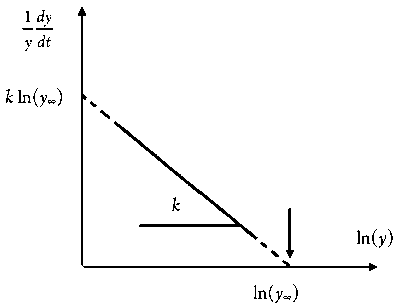
Рис. 8. Определение предела роста у _∞ и параметра k

Представим уравнение (2) в виде dy = Ae ~ ktdt.(5)

y

Интегрируя (5), получим

Iny = ——e kt + InC.

При t ^ ^ имеем y ^ y max . Поэтому из (6) получаем In C = In y max . Тогда из (6) следует

In y — ln ymax =-Ae - kt.(7)

k

Гадзаов А.Ф., Кузьмин В.И., Самохина А.С. Математические модели динамики...

Следующую анаморфозу получаем из уравнений (2), (7):

¹ dy = k ^(ln у max - ^ln у ).

y dt

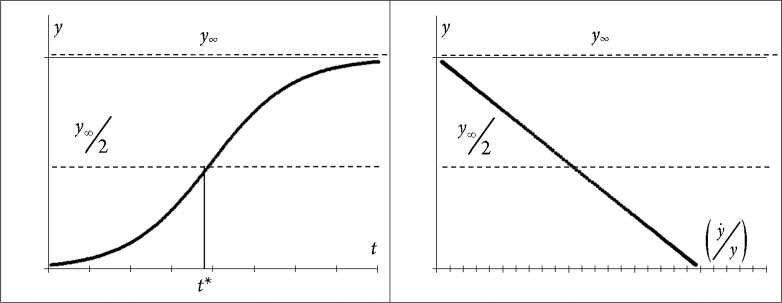
Таким образом, анаморфозой, соответствующей линейной зависимости между харак теристиками системы, являются координаты —— и ln(у). По углу наклона линейного y dt участка зависимости определяем значение параметра k (рис. 8). Продолжение линейного участка до пересечения с осью абсцисс позволяет определить значение ln уmax.

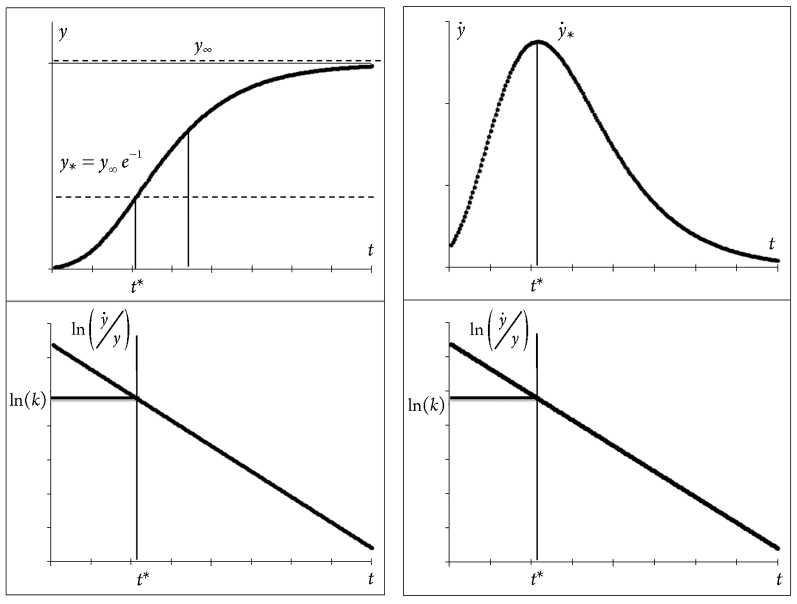
Структурная схема анаморфоз, используемая для оценки параметров моделей ограни- ченного роста Гомперца, представлена на рисунке 9.

^Из ⁽²⁾, ⁽⁴⁾, ⁽⁷⁾ получим у ⁽ t 0 ) = ¹ у max

.

e

Логарифм угла наклона прямой для данных в координатах t ,ln ( у / у ) позволяет определить наступление максимума. На рисунке 9- а отмечено положение пика на интегральной кривой, на рисунке 9- б – на кривой скорости.

а

б

Рис. 9. Структурная схема анаморфоз используемая для оценки параметров моделей ограниченного роста модели Гомперца: а – интегральной кривой; б – кривой скорости

Логистическая модель. При f ( t, у ) = ky (1 — у / у _max ) - это логистическая модель (рис. 10–11), которая стала основой теории цепных реакций Н.Н. Семёнова [4], удосто-

Выпуск 3/2020

енной Нобелевской премии, где y _max – предел роста. Вдали от предела доминирует процесс типа расширенного воспроизводства, а при приближении к пределу процесс протекает под влиянием прессинга исчерпания ресурса.

Знание параметра логистического уравнения k позволяет по известному пределу роста определять положение точки максимума функции и накопленный уровень в точке перегиба.

Из исходного уравнения логистической модели получается анаморфоза dy-=k fl -    \ ydt ( У max J dy

Это уравнение определяет линейную зависимость в координатах    ~ y .

ydt

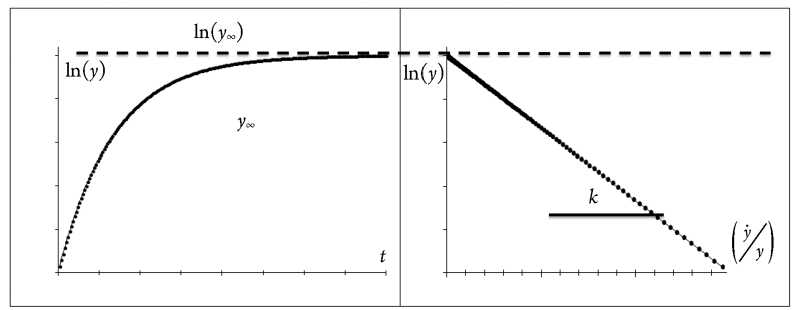
В результате пересечения линейной зависимости с осью абсцисс определяется предел роста (рис. 12- б ).

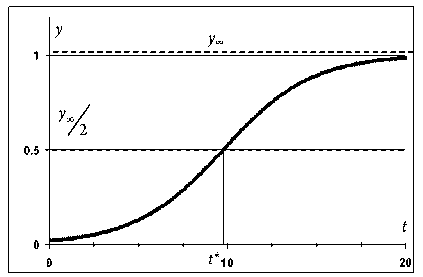
Рис. 10. Интегральная кривая логистической модели

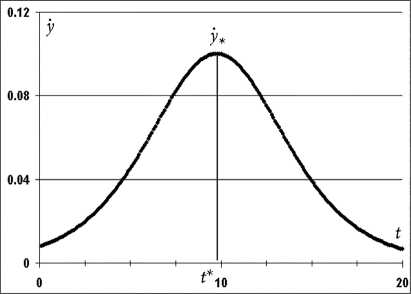
Рис. 11. Кривая скорости логистической модели

Другой набор анаморфоз, представленный на рисунке 12, позволяет определить значение горизонтальной асимптоты, соответствующей пределу роста общего числа случаев. Структурная схема на рисунке 12- а позволяет определить предел роста для модели Гом-перца, схема на рисунке 12- б – для логистической модели.

Гадзаов А.Ф., Кузьмин В.И., Самохина А.С. Математические модели динамики...

а

б

Рис. 12. Структурная схема анаморфоз, используемая для оценки предела роста: а – модели Гомперца; б – логистической модели

Применение метода анаморфоз к реальным данным для определения параметров модели

Принадлежность реальных данных к определенному типу моделей ограниченного роста устанавливается на основании использования анаморфоз и определения линейной зависимости, определяющих принадлежность процесса к определенному типу модели.

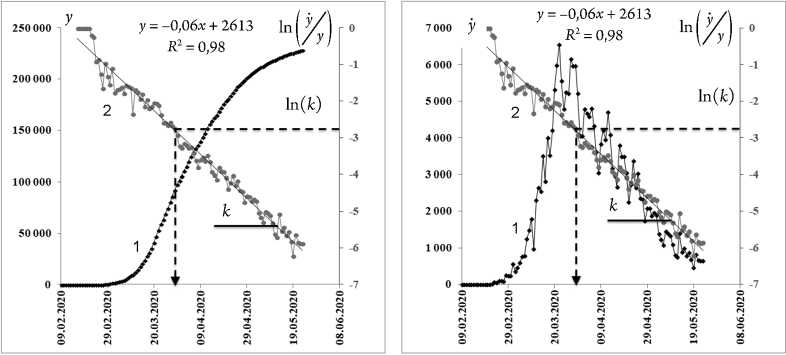
В качестве примера содержательность анаморфоз для оценки динамики коронавируса представлена по данным о динамике этого вируса в Италии (рис. 13).

Горизонтальной линией отмечено значение логарифма коэффициента наклона прямой, что соответствует максимума по модели Гомперца.

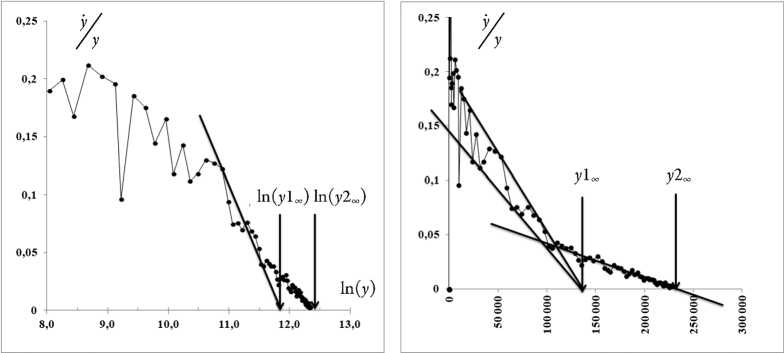
Для данных рисунка 6 применение анаморфоз рисунка 12 представлено на рисунке 14.

По представленным на рисунке 14 данным видно, что присутствуют две волны. Для первой волны у_∞ = 130–140 тыс. человек, а идущая в след вторая волна дает оценку порядка 230 тыс.

Один из параметров этой модели ( у_∞ ) равен предельному числу подверженных данному заболеванию людей на данной стадии эпидемического процесса и определяется численностью популяции.

Выпуск 3/2020

а                                              б

Рис. 13. Линией 1 обозначены данные динамики вируса в Италии, линией 2 – анаморфоза для его динамики: а – интегральной кривой; б – кривой скорости

а                                              б

Рис. 14. Определение пределов роста для данных рисунка 6 по модели Гомперца: а – (y1_∞ = 130 000 и y2_∞ = 225 000); б – логистической модели (y1_∞ = 140 000 и y2_∞ = 230 000)

Второй параметр ( k ) равен обратной величине характерного времени процесса, т.е. интервалу от точек перегиба до точек максимума (рис. 12). Характерное время зависит как от природно-климатических условий [13], так и организации процесса противодействия распространению эпидемий (сокращению числа контактов с инфицированными, эффективностью лечения зараженных и т.п.).

Исключение тренда

Общие характеристики развития включают данные как о трендах, так и колебаниях относительно трендов.

Гадзаов А.Ф., Кузьмин В.И., Самохина А.С. Математические модели динамики...    13

Задача исключения тренда была решена в [1; 2; 3; 4; 10] и привела к разработке согласованного алгоритма решения этой проблемы путем построения обобщенной сдвиговой функции, решающей проблему согласования метода исключения тренда и колебаний, наиболее близких к периоду [4].

При этом периодические компоненты в данных о динамике y(t k ) (где tk - моменты регистрации измеряемой характеристики) можно определить, воспользовавшись преобразованием исходного ряда в новый ряд по формуле

y ( t k - ^А t m ) • y ( t k ^+А t m ) х ⁽ t k )=in^-------------^L,

y ⁽ t k )

где y ( t k — A t m ) , y ( t k ) , y ( t k + А t m ) - значения в соответствующие моменты времени; A t m - фиксированный пробный временной интервал. Результатом преобразования является ряд х ( t k ) с близким к нулю значением математического ожидания, для которого вычисляется сдвиговая функция [9] по формуле

1 n—k a (Tk )=n-kHx( t,+t)—x( tj) • j=1

Приведенная формула (10) используется для дискретного временного ряда χ(t) на ин-jT тервале длительностью T (исходного ряда данных). Интервал дискретизации равен n — 1 (где n – общее число отсчетов функции) и определяет точность измерений динамики по T времени. Здесь Ok = k--- - пробный период, 1 < k < 3/4n. Минимумы этой функции n — 1

определяют наиболее близкие к периодам временные интервалы, называемые почти пе- риодами [5]. Следует отметить, что задача оптимизации этой функции по Δtm приводит к определению обобщенной сдвиговой функции a(τk, Δtm). Для оценки грубости получаемых величин почти периодов в [2] был введен класс сдвиговых функций в соответствии с метриками функционального анализа [1].

Влияние способа исключения тренда на результаты, близкие к периодическим компонентам, по фактам их анализа известно как эффект Слуцкого – Юлла [3], поэтому для минимизации такого влияния была введена [2] обобщенная сдвиговая функция, позволяющая согласовать характеристики процесса исключения тренда и значения, наиболее близкие к его периодическим компонентам. Таким образом, появляется возможность на основе анализа результатов измерений, представляющих некоторую трендовую динамику с колебаниями, получить параметры процессов, характеризующих механизмы формирования их общей структуры на нижнем и верхнем уровнях.

Результат исключения тренда из данных по заболеваемости в Италии и сдвиговая функция для отклонений от тренда представлены на рисунках 15–16.

Здесь выделяются два почти периода: 7 дней и 42 дня (1,5 месяца). Периоды в 7 дней могут быть результатом цикличности в проведении новых тестов (рис. 17).

Аналогичные зависимости для динамики этого процесса в США представлены на рисунке 18.

На рисунке 19 представлены анаморфозы рисунка 5 для данных рисунка 12.

Горизонтальной линией отмечено значение логарифма коэффициента наклона прямой, что соответствует максимуму по модели Гомперца.

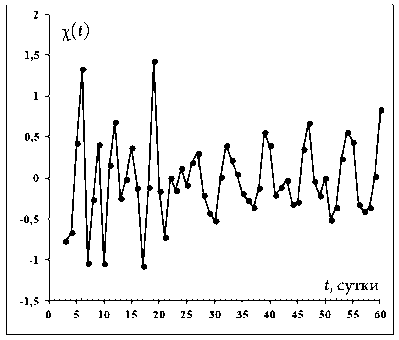
Рис. 15. Результат исключения тренда из данных рисунка 4 числа новых случаев

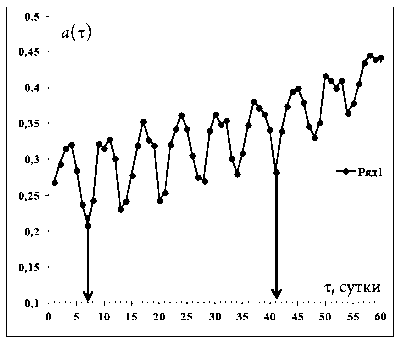
Рис. 16. Сдвиговая функция для данных рисунка 15

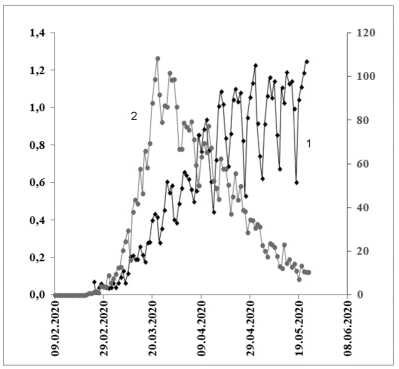
Рис. 17. Сопоставление количества новых тестов на 1000 человек в Италии (линия 1) и новых случаев заболеваний (линия 2) на 1 млн человек

Гадзаов А.Ф., Кузьмин В.И., Самохина А.С. Математические модели динамики...

1 - Общее число случаев

1000 000

1800 000

1600 000

1400 000

1200 000

400 000

200 000

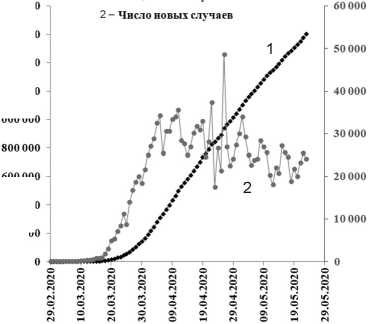
600 000

б

Рис. 18. Динамика заболеваемости коронавирусом в США: а – линейный масштаб; б – логарифмический масштаб по оси ординат

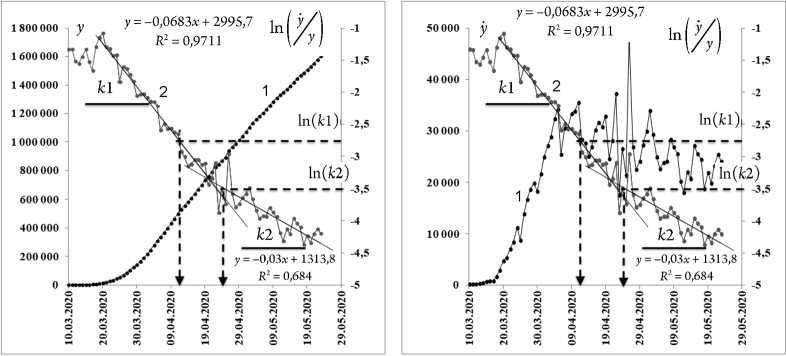
а                                              б

Рис. 19. Линией 1 обозначены данные динамики вируса в США, линией 2 – анаморфоза для его динамики: а – интегральной кривой; б – кривой скорости

На рисунке 19 выделяются 2 волны и время наступления максимума количества заболевших за единицу времени для каждой из волн.

Для определения пределов роста заболевших воспользуемся анаморфозами, представленными на рисунке 12. На рисунке 20, как и на предыдущих анаморфозах, выделяются 2 волны.

Отметим, что величины пределов по модели Гомперца и логистической модели отличаются. Результат исключения тренда из данных по заболеваемости в США и сдвиговая функция для отклонений от тренда представлены на рисунке 21.

Здесь выделяются два почти периода – 7 дней и 42 дня (1,5 месяца), которые выделены на рисунке 22.

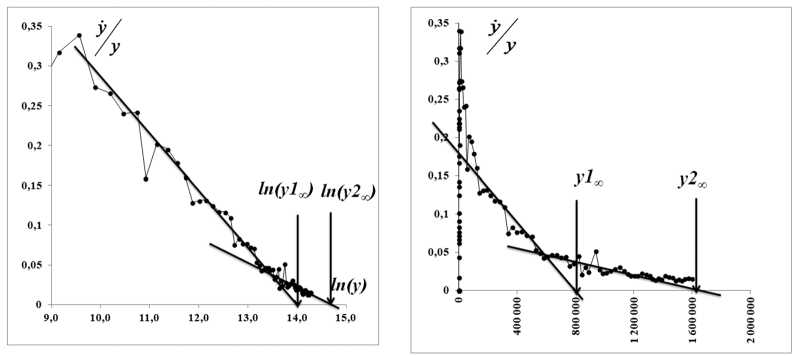
б

а

Рис. 20. Определение пределов роста для данных рисунке 6 по модели Гомперца ( а ) ( y 1 _∞ =1 202 000 и y 2 _∞ =2 420 000) и логистической модели ( б ) ( y 1 _∞= 800 000 и y 2 _∞ =1 600 000)

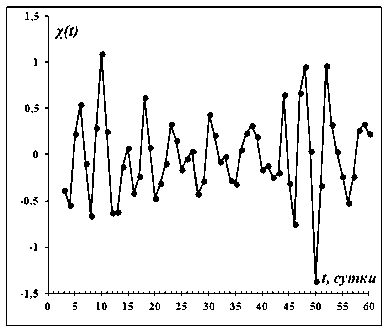
Рис. 21. Результат исключения тренда из данных рисунка 4 числа новых случаев

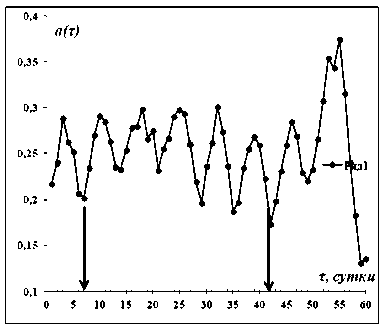
Рис. 22. Сдвиговая функция для данных рисунка 4

Гадзаов А.Ф., Кузьмин В.И., Самохина А.С. Математические модели динамики...

Анализ мировых данных эпидемии коронавируса

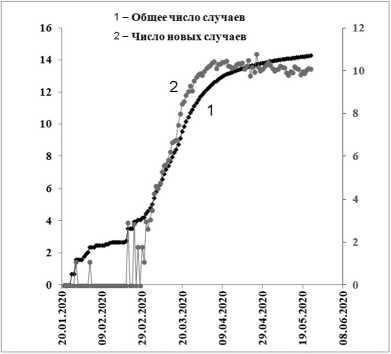
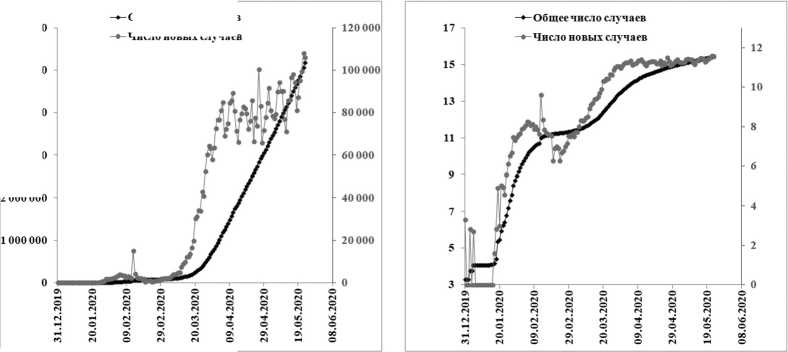
Более сложной динамикой отличаются мировые данные по заболеваемости (рис. 23).

Общее число случаев

6 000 000

Число новых случаев

5 000 000

4 000 000

3 000 000

2 000 000

б

а

Рис. 23. Динамика заболеваемости коронавирусом в мире: а – линейный масштаб; б – логарифмический масштаб

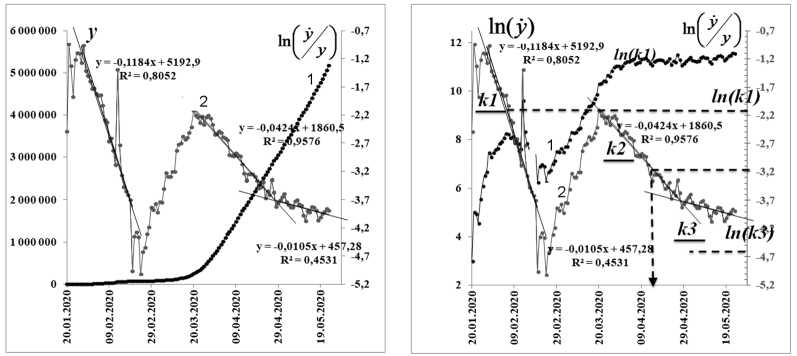
Построение в таких координатах позволяет выявлять последовательность стадий развития процесса на уровне мировой эпидемии (рис. 24). Здесь очевидна реализация периода индукции стадии небольшим количеством вовлеченных в процесс людей с переходом к следующей стадии, когда была реализована мировая эпидемия.

а

б

Рис. 24. Линией 1 обозначены данные динамики вируса в США, линией 2 – анаморфоза для его динамики: а – интегральной кривой; б – кривой скорости

Горизонтальной линией отмечено значение логарифма коэффициента наклона прямой, что соответствует максимуму по модели Гомперца

Выпуск 3/2020

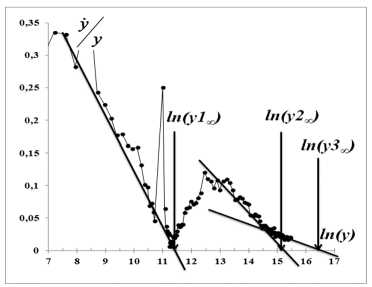
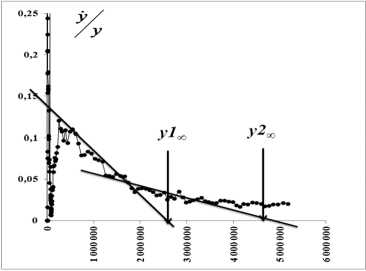
Для определения пределов роста заболевших воспользуемся анаморфозами, представленными на рисунке 12. На рисунке 25 для модели Гомперца выделяются 3 предела (рис. 25- а ), а для логистики –2 предела (рис. 25- б ).

а

Рис. 25. Определение пределов роста для данных рисунка 6 по модели Гомперца ( а ) ( y 1 _∞ = 100 000 тыс., y 2 _∞ = 4 000 000, y 3 _∞ = 14 500 000) и логистической модели ( б ) ( y 1 _∞ = 270 000 и y 2 _∞ = 4 800 000)

б

Произошел запуск второй стадии эпидемии, который ведет процесс к общему количеству заболевших – 14,5 млн человек.

Отметим, что представленная система анаморфоз позволяет определять момент времени наступления новой стадии развития заболевания. Результат исключения тренда из данных по заболеваемости в мире и сдвиговая функция для отклонений от тренда представлены на рисунках 26–27.

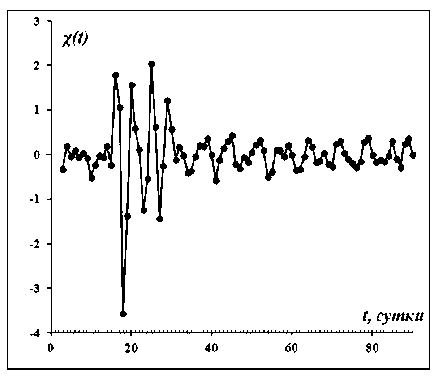
Рис. 26. Результат исключения тренда из данных рисунка 23 числа новых случаев

Здесь выделяются те же два почти периода – 7 дней и 42 дня (1,5 месяца), которые выделены на рисунке 22.

Гадзаов А.Ф., Кузьмин В.И., Самохина А.С. Математические модели динамики...

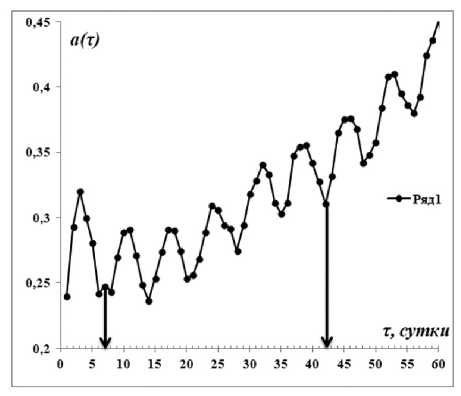
Рис. 27. Сдвиговая функция для данных рисунка 6

В принципе рассматриваемые модели ограниченного роста содержат 2 параметра, нормировка по которым характеристик процессов, рассмотренных выше, приводит к единой зависимости (рис. 28).

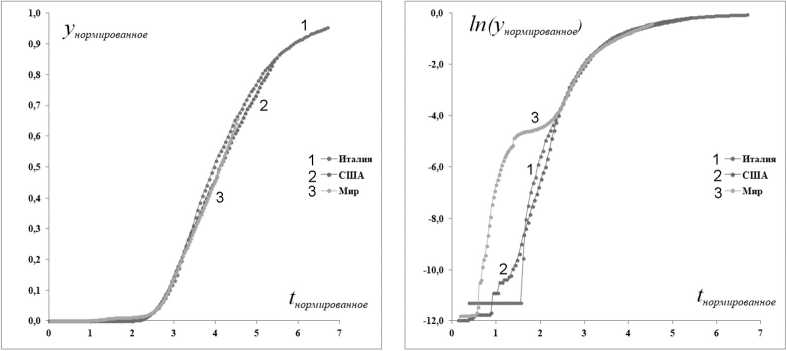
Рис. 28. Данные по количеству заболевших в мире, США и Италии, нормированные по уровню и времени

На рисунке 29 представлено число случаев заболевания на 1 млн человек ( Y ) и число тестов на 1000 человек ( X ).

На рисунке 30 представлена анаморфоза для данных рисунка 29; здесь достигается спрямление в координатах X ~ 1n( Y max — Y ), что соответствует модели

Y = Y _max – Cexp ^{( –kt )} .

Процесс перешел в другую фазу, фиксируется момент смены состояний.

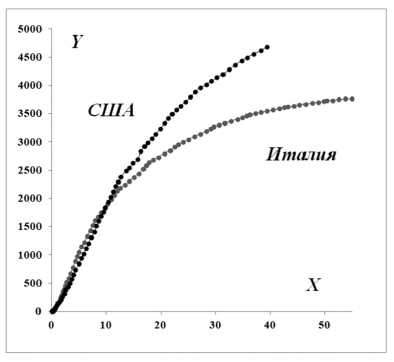
Рис. 29. Италия, США: Y – число случаев заболеваний на 1 млн человек; X – число тестов на 1000 человек

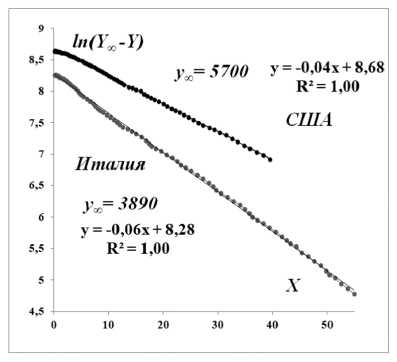
Рис. 30. Спрямляющее преобразование для данных рисунка 29

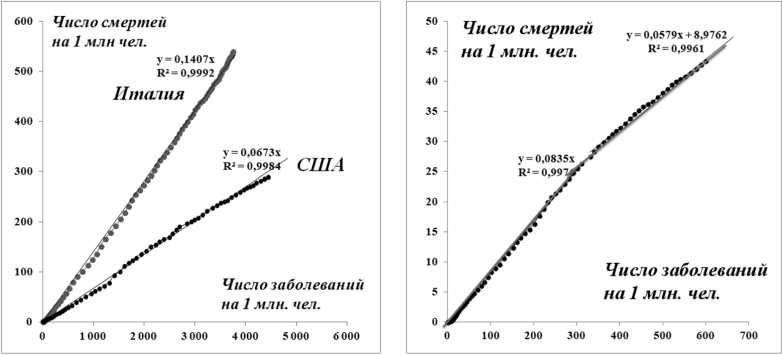
Рис. 31. Италия – сдвижка 3 дня; США – 6 дней; мир – 5 дней

Гадзаов А.Ф., Кузьмин В.И., Самохина А.С. Математические модели динамики...    21

Таким образом, на один смертельный случай приходится 7 заболевших в Италии и 15 заболевших в США; для мира в целом – один смертельный случай на 13 заболевших.

Полный набор связей характеристик процесса представлен для Италии на рисунке 32.

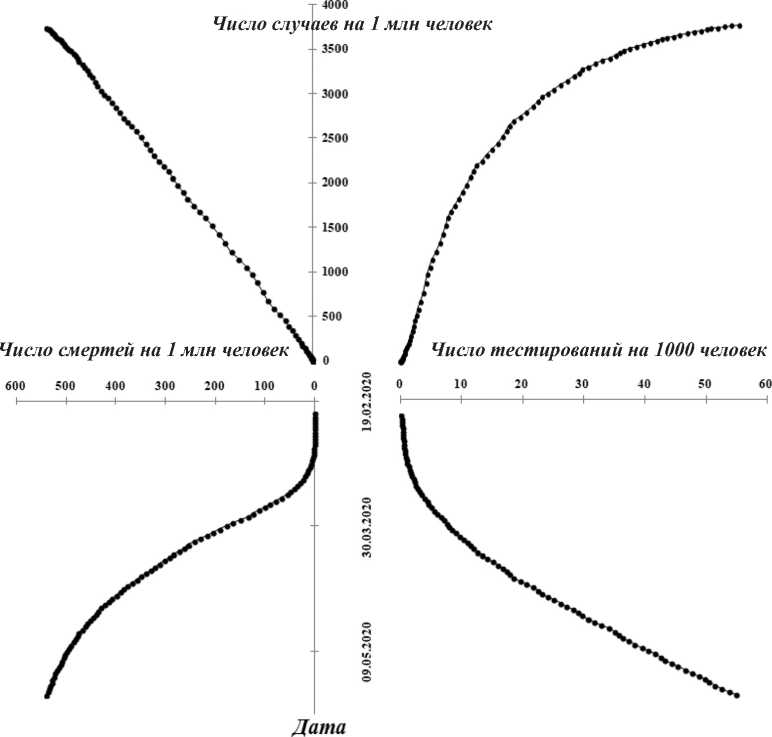
Рис. 32. Полный набор связей характеристик процесса для Италии

Заключение

Результаты исследования показали, что динамика эпидемий представлена последовательностью стадий, каждая из которых соответствует процессу ограниченного роста, для которого рост числа заболевших ограничен фиксированным пределом, а ежедневное число новых случаев заболеваний представлен унимодальной кривой.

Такие процессы часто описываются двухпараметрическими зависимостями, один из параметров которых характеризуется пределом роста общего числа заболеваний, а второй определяет характерное время процесса, показывающее период выхода процесса к максимальному числу ежедневной заболеваемости.

Принадлежность процесса к определенной модели ограниченного роста и оценка ее параметров определяются системой нелинейных преобразований исходных данных о динамике системы, переводящих их в линейные зависимости. Рассмотрение реальной динамики заболеваемости коронавирусом в Италии, США и мире в целом показало, что это процессы, соответствующие экспоненциальному убыванию темпа роста заболеваемости (модель Гомперца). Нормировка динамики заболеваемости для рассмотренных систем по параметрам показала идеальное совпадение кривых роста, что является свидетельством того, что результаты измерений объективно характеризуют динамику рассматриваемой эпидемии.

22 в ыпуск 3/2020

Это показывает, что для популяции существует объективный предел подверженности населения заболеванию данного типа. Эти результаты воспроизводились на данных о динамике заболеваемости в Швеции, Испании, Португалии, Франции, Норвегии, Исландии, Китае, Южной Корее, Японии и других странах.

В связи с тем что реальная динамика сложных систем представлена трендами и колебаниями, был использован алгоритм исключения трендов, обеспечивающий колебания относительно нуля с практически нулевой средней, а для полученного ряда определялись значения, наиболее близкие к периодам. Для всех рассмотренных данных эти значения совпали и составили недельный и полуторамесячный циклы. Полуторамесячный цикл составляет половину трехмесячного сезонного цикла, который не мог быть выявлен по динамике коронавируса в связи с малым временем наблюдения. Однако на многолетних данных о развитии пневмонии в США явно выделяются годичный и двенадцатилетний циклы, которые показывают наличие иерархии циклов, длительность которых варьируется в широком диапазоне. При этом в зависимости от внутренних и внешних условий внутри годичного цикла процесс может проходить ряд стадий ограниченного роста.

Рассмотрение влияния количества тестов на число зафиксированных случаев заболеваемости показало (двумя анаморфозами), что это процесс, для которого существует предел общего числа зафиксированных заболевших. Полученные оценки предела общего числа заболевших по двум анаморфозам модели Гомперца и по зависимости числа зафиксированных заболевших от количества тестов практически совпали. Это подтверждает объективность получаемых оценок.

Была установлена зависимость числа смертельных случаев от общего числа заболевших в момент, смещенный относительно данного на период, обеспечивающий линеаризацию зависимости. Это позволило представить структуру процесса прогнозирования заболеваемости как состоящую из входа по количеству тестов в данный момент времени, определяющему общую зафиксированную заболеваемость, по которой, в свою очередь, возможно определить смертность.