Математические модели динамики регионального бизнеса

Введение. Дифференциация уровня жизни городского и сельского населения продолжает оставаться значительной. Жители небольших населенных пунктов либо недополучают часть услуг, либо их выбор существенно ограничен. В работе показано, что появление в сельском регионе предприятий, продукция (услуги) которых востребована за пределами региона, может привести к появлению и устойчивому функционированию предприятий малого бизнеса, оказывающих услуги жителям региона и, соответственно, к успешному экономическому развитию данного региона.

• 1.    Построение и исследование математических моделей. Будем считать, что трудоспособное население сельского региона состоит из двух частей. Первая часть работает в сфере услуг для населения региона (малый бизнес), множество предприятий такого типа обозначим X. Вторая часть трудоспособного населения работает на предприятиях, производящих продукцию и оказывающих услуги для населения за пределами региона.

• (с) В.П. Савельев, Н.И. Сутягина, 2021

  

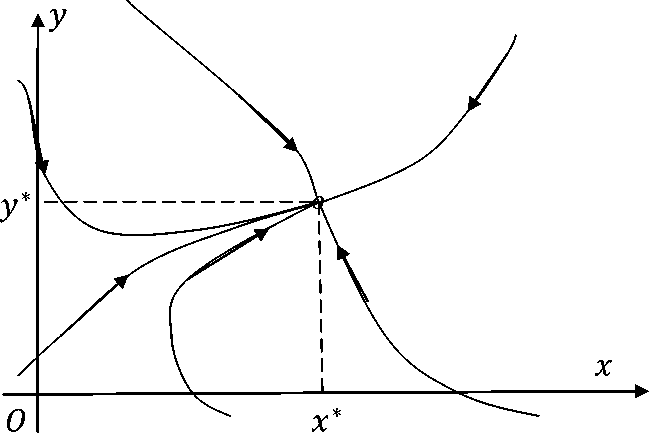
  Рис. 1. Фазовый портрет линейной системы (1)

  
  

Совокупность предприятий такого типа обозначим Y. Для построения математической модели, описывающей динамику финансовых потоков, введем понятие состояния динамической системы. Отметим, что Ю. И. Неймарк при построении простых математических моделей [1-3] придавал первостепенное значение выбору фазовых переменных и соответствующего фазового пространства. Под состоянием системы будем понимать двумерную функцию времени (x(t),y(t)), г де x(t) — объем предоставляемых услуг (в денежном выражении) предприятиями типа X, a y (t) — объем произведенных товаров и предоставленных услуг предприятиями типа Y.

• 1.1.    Линейная модель. Составим систему линейных дифференциальных уравнений, позволяющую анализировать сферу услуг жителям сельского региона.

{ x = —ax + by, y = R + dx — cy,

в которой все параметры положительны. Слагаемые в правых частях уравнений означают (в единицу времени): ax — оплата труда работников внутреннего сервиса за вычетом их затрат на свой продукт, by — доход системы предприятий типа X от работников предприятий типа Y, R — доход предприятий типа R от продажи товаров и услуг на внешнем рынке, dx — доход предприятий типа, Y от работников предприятий типа X. cy — оплата, труда работников предприятий типа Y за вычетом их затрат на свой продукт.

При естественном предположении, что c >  b, a > d, суммьi денег (a — d)x и (c — b)y тратятся жителями региона на покупку товаров и услуг вне данного региона. Фазовым пространством динамической системы (1) является неотрицательный квадрант K = {(x,y) G R2: x > 0, y > 0}. Нетрудно видеть, что состояние равновесия ( aC — bd , aC — bd ) спстемы (1) является устойчивым узлом. Соответствующий фазовый портрет системы (1) представлен на рис. 1.

Заметим, что поведение траекторий на положительной полуоси Ox определяется вектором (5с,y) = (— ax, R + dx) Это значит, что траектории системы (1) пересектот ось Ox снизу вверх, так как y = R + dx > 0. Поведение траекторий на положительной полуоси Oy определяете я вектором (X ,y = (by,R + cy) Это значит, что траектории пересекают ось Oy слева направо, так как X = by >  0. Таким образом, для любого начального условия (x₀,y₀) Е K фазовая траекторпя (x(t),y(t)) не выходит из фаз<звого пространства. K.

• 1.2.    Нелинейная модели 1. В линейной модели (1) предполагалось, что доход by системы предприятий типа X зависит лишь от объема y произведенных товаров и услуг предприятиями типа Y. Однако, такое предположение справедливо лишь при постоянном объеме xy услуг малого бизнеса. Очевидно, что доход зависит и от объема x, то есть равен bxy. В соответствии с этим составим систему нелинейных дифференциальных уравнений

{ 5с = -ax + bxy,

y = R + dx — cy — bxy, в которой слагаемое cy означает теперь оплату труда работников предприятий типа Y за вычетом их затрат не только на свой продукт, но и затрат на внутренний сервис bxy. При естественном предположении, что a > d, суммьi денег (a — d)x и cy тратятся на покупку товаров и услуг вне данного региона. Динамическая система (2) имеет два состояния равновесия: 1) (0,R), 2) (Rb—ac , a)- При условии Rb — ac > 0 оба состояния равновесия находятся в фазовом пространстве K.

Как известно [4], для исследования состояния равновесия нелинейной системы требуется ее линеаризовать в окрестности состояния равновесия. В окрестности первого состояния равновесия (0,R) линеаризоваиная система (2) имеет вид:

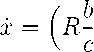
— a) x + 01 y —

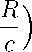
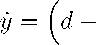
R x - c y -

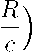
Собственные числа матрицы легко находятся:

Ai — R— — a >  0,    A2 — — c <  0.

c

Так как собственные числа матрицы действительные и разных знаков, состояние равновесия (0, R) является седлом.

В окрестности второго состояния равновесия линеаризованная система (2) имеет вид:

5с = 0 x —

Rb

- ac

b ( a — d )

+

Rb - ac a - d

y

-

a \ b,

y = (d — a) (x —

Rb - ac b ( a — d )

Rb - cd

a

- d

y

-

a b.

Уравнение для собственных значений матрицы имеет вид:

Рис. 2. Фазовый портрет системы (2) и системы (6) с устойчивым фокусом

А² +--— А + Rb — ac = 0.                           (5)

a-d

Поскольку Rb — ac >  0, a > d, то и Rb — cd >  0. Это значит, что собственные числа либо оба действительные и отрицательные, либо комплексно-сопряженные с отрицательной действительной частью. Таким образом, состояние равновесия ( R - Oc , ;) является или устойчивым узлом, или устойчивым фокусом. Соответствующий устойчивому фокусу фазовый портрет системы (2) представлен на рис. 2.

Поведение траекторий на положительной полуоси Ox определяете я вектором (5с, y) = (— ax,R + dx) Это значит, что тратсторпп пересекают ось Ox снизу вверх, так как y = R + dx > 0. Поведение траекторий на положительной полуоси Oy определяется вектором (x , y) = (0, R—cy) а также собственным вектором (0,1)T, то есть обе ш — сепаратрисы седла (0, R) лежат на положительной полуоси Оу. Тот факт, что для любого начального условия (x₀,y₀) € K фазовая траекторпя (x(t),y(t)) нс выходит из <1>азового пространства, K. служит косвенным признаком того, что математическая модель (2) адекватно описывает динамику финансовых потоков (x(t),y(t)).

Далее, предположим, что Rb — ac <  0. Это значит, что либо поступления R недостаточные, либо коэффициенты a и c, характеризующие оплату труда, велики, либо люди слабо пользуются услугами внутреннего сервиса (коэффициент b невелик). В этом случае состояние равновесия (0, R) становится устойчивым узлом, а состояние равновесия (Rb - ac , a) — седлом, но оно расположено вне фазового пространства. Соответствующий фазовый портрет представлен на рис. 3.

Заметим, что из любой начальной точки фазового пространства x(0) = x0 > 0, y(0) = y0 > 0 все траектории входят в устойчивый узел (0,R). Это значит, что не имеется достаточных ресурсов для поддержания регионального сервиса, он исчезает.

• 1.3.    Нелинейная модель 2. В моделях (1) и (2) предполагалось, что внешний доход R предприятий типа Y является постоянной величиной. Однако, такое положение дел соответствует ситуации, когда, в регионе имеются лишь бюджетные организации. При наличии

  

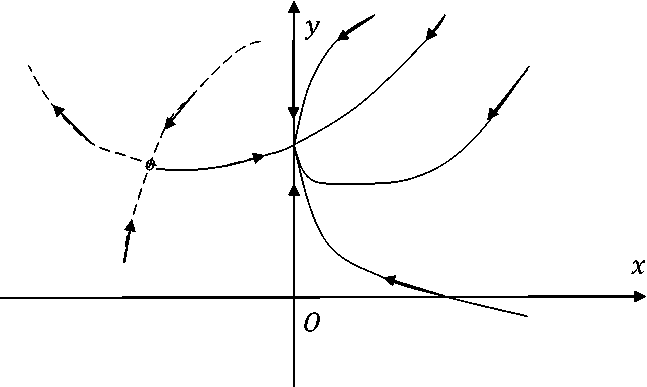
  Рис. 3. Фазовый портрет системы (2) при условии Rb — ac < 0, и системы (6) при условии Rb² + ab(p — c) — ea² < 0

  
  

в регионе коммерческих предприятий естественно предположить, что с ростом объема выпускаемой продукции (услуг) доход от их продажи на внешнем рынке будет увеличиваться, то есть имеет вид R + py, p > 0. Если же учесть, что с ростом объема товаров и услуг цены несколько снижаются, то предлагается доход задать в виде R + py — ey², p >  0, e >  0.

Тогда динамику изменения финансов можно представить в виде несколько измененной системы (2)

{ x = —ax + bxy,

y = R + (p — c)y — ey2 + dx — bxy, в которой, кроме неравенства a — d > 0, будем предпслагать, что p — c < 0.

Система (6) имеет в фазовом пространстве K два состояния равновесия: (p-^c)+V(p^-c)²+^4eR                        -

• 1)    (0,y_i), г де y_i = -----^"2^--положительный корень уравнения

ey² + (c — p)y — R = 0,                               (7)

• 2)    (xi,a).r,^ = '

Заметим, что состояние равновесия (xi,^) принадлежит фазовому пространству при выполнении неравенства

Rb² + ab(p — c) — ea² > 0.

В окрестности первого состояния равновесия (0, yi) линеаризованная система имеет вид:

J x = (byi — a)x + 0(y — yi),

( y = (d — byi)x — p(—c)2 + 4eR(y — yi).

Собственные значения матрицы линейной системы (9) легко находятся:

Л1 — byi - а, ^2 — - р(p - c)² + 4eR .

Заметим, что выражения by1 — а и Rb² + ab(p — c) — eg? имеют одинаковый знак:

by 1 - a —

b(p - c) + bр(р — c)² + 4eR       bp(p - c)² + 4eR — (b(c — p) + 2ea)

2e               a =                2e b2((p - c)2 + 4eRb(c — p) + 2ea)2              Rb2 + ab(p — c) — ea2

2e[bp (p — c)² + 4eR + b(c — p) + 2ea]     bp (p — c)² + 4eR + b(c — p) + 2ea

При условии (8) собственные значения (10) будут действительными и разных знаков, то есть, состояние равновесия (0, y1) — седло.

В окрестности второго состояния равновесия (x1, а) линеаризованная система имеет вид:

x — 0(x — x1) + bx₁ yy y — (d — a)(x — x1) —

-

a b

Rb² + bd(p — c) + ea(a — 2d) , a.

(a — d)b          ^y — V'

Уравнение для собственных значений матрицы линейной системы (11) имеет вид:

Л2 ₊ Rb ² ₊ М(р — с ) + ^еа(а — 2 d ) л _{+ (}а — d₎bxi — о,               ₍12)

(а — d)b

При выполнении условий а — d >  0, p — c <  0, выполняется неравенство

Rb + bd(p — c) + ea(a — 2d) >  Rb + ab(p — c) — ea > 0,             (13)

поэтому корни уравнения (12) либо оба действительные и отрицательные, либо комплексно-сопряженные с отрицательной действительной частью. Это значит, что состояние равновесия (x1, а) является устойчивым узлом или фокусом. Соответствующий устойчивому фокусу фазовый портрет системы (6) представлен на рис. 2.

При уменьшении параметра R выполнится неравенство Rb2 + ab(p — c) — ea2 < 0. В этом случае второе состояние равновесия системы (6) не принадлежит фазовому простран-(p-c) + A/(p-c)2+4eR ству, а первое состояние равновесия I 0,-----^г) становится устойчивым узлом

(рис. 3). Это значит, что не имеется достаточных ресурсов для поддержания региональ ного сервиса, он исчезает.

Выводы.

• 1)    Результаты исследования линейной модели (1) и нелинейных моделей (2) и (6) хо

рошо согласуются.

• 2)    Из исследования линейной модели следует: а) наличие в регионе предприятий типа Y работающих на „экспорт", является достаточным условием для возникновения и устойчивого функционирования малого бизнеса; Ь) для увеличения объема услуг малого бизнеса, x — adb - bc надо сократтсать разшщу между a ii c. а также между d ii b. то есть уменьшать суммы денег (a — c)x, (d — b)y, которые тратятся на покупку товаров и услуг

вне региона.

• 3)    Из исследования нелинейных моделей следует: а) начиная с достаточно большого объема товаров и услуг R, производимых в единицу времени предприятиями типа Y,

появляется возможность для возникновения и устойчивого функционирования малого бизнеса; Ь) для увеличения объема услуг малого бизнеса x = R-Jc надо сокращать разницу между а и d, и уменьшать коэффициент с, то есть уменьшать суммы денег (a — d)x и су, которые тратятся на покупку товаров и услуг вне региона.