Математические модели функций преобразования для системы кластеров измерительных преобразователей давления

В работе [1] показана возможность объединения измерительных преобразователей (ИП) давления, обладающих близкими метрологическими характеристиками, в кластеры. Можно предположить, что в рамках одного кластера существуют математические модели функции преобразования (ФП), позволяющие получить меньшую величину приведенной погрешности ИП, чем при использовании единой модели ФП для всей партии преобразователей в целом. В статье рассматриваются вопросы нахождения моделей ФП внутри кластеров измерительных преобразователей, что позволяет увеличить метрологический запас [2] преобразователей давления по приведенной погрешности.1

Постановка задачи. Современная технология производства микропроцессорных ИП давления предполагает использование единой ММ для ИП одного конструктивного исполнения [3]. Рассмотрим 2-факторную модель функции преобразования ИП давления следующего вида:

P = P 0 ( в о + P 1 1 + P 2 1 ² + P 3 t ³ + в 4 1 ⁴ + p 5 1 ⁵ ) +

^{+ p} 1 ( ^p 6 ^{+ P} 7 t ^{+ P} 8 t 2 ^{+ P} 9 t 3 ⁺ P 10 t 4 +P 11 t 5 ) ⁺

+ P 2 ( P 12 + P 13 1 + P 14 1 2 + P 15 1 3 + P 16 1 4 + P 17 1 5 ) +

^{+ p} 3 ( ^P 18 ^{+ P} 19 t ^{+ P} 20 t 2 ^{+ P} 21 t 3 ^{+ P} 22 t 4 ^{+ P} 23 t 5 ) ⁺

^{+ p} 4 ( ^P 24 ^{+ P} 25 t ^{+ P} 26 t ^{2 + P} 27 t 3 ^{+ P} 28 t 4 ^{+ P} 29 t 5 ) ⁺

^{+ p} 5 ( ^P 30 ^{+ P} 31 t ^{+ P} 32 t ^{2 + P} 33 t ^{3 + P} 34 t ^{4 + P} 35 t 5 ) , ⁽¹⁾ где P - рассчитанное давление; P - вещественные коэффициенты; p – нормированный код давления на выходе ИП; t – нормированный код температуры, окружающей измерительный преобразователь, среды.²

Использование полной математической модели (1) на практике маловероятно вследствие того, что полная модель не обеспечит заданный класс точности ИП при проведении процедуры верификации [4].

Целью данной работы является нахождение вида моделей функции преобразования для измерительных преобразователей давления, входящих в кластеры А, В и С, описанные в [1].

Для достижения поставленной цели необходимо реализовать следующие задачи:

• 1.    Предложить метод предварительного формирования вида ММ ФП.

• 2.    Разработать метод уточнения вида предварительно сформированной модели ФП и создать алгоритм реализации этого метода.

• 3.    Разработать алгоритм формирования вида ММ ФП методом «исключения».

• 4.    Применить методику оценки сложности ММ ФП.

Метод предварительного формирования вида модели ФП

Метод срезов позволяет осуществить предварительное формирование модели путем определения максимальной степени вхождения факторов температуры p и давления t в математическую модель. Суть метода заключается в «разрезании» пространственной ФП на заданном уровне одного из факторов (см. рисунок) и аппроксимации полученного «среза» полиномами последовательно возрастающих степеней. Степень аппроксимирующего полинома, обеспечивающая заданный уровень погрешности аппроксимации, признается оптимальной для данного «среза». Проводя «разрезания» пространственной ФП, получаем набор степеней факторов, на основании которых осуществляется предварительное формирование математической модели функции преобразования ИП давления.

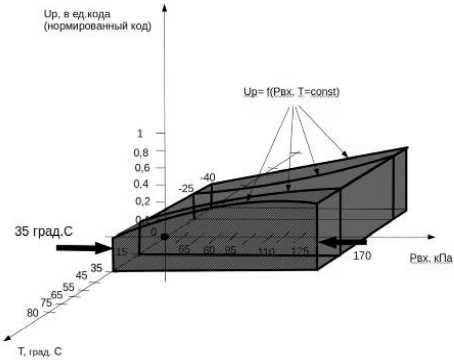
Пример среза пространственной модели ФП по температуре

Применение метода «срезов» к ИП кластеров А, В и С [1] позволило получить приведенные ниже предварительные модели:

• 1.    Для кластера А:

P = P 0 ( в о + 3 1 t + k 1 ² + 3 э t ³ ) +

• +P1 (36 + 37t + 38t2 + 39t3 ) +

• ⁺ P ² ( ³ 12 ⁺ 3 13 t ⁺ 3 14 t ^{2 +} 3 15 t 3 ) ⁺

• ⁺ P 3 ( ³ 18 ⁺³ 19 t ^{+ 3} 20 t ^{2 +3} 21 t ³ ) .                 ⁽²⁾

• 2.    Для кластера В:

P = p ⁰ ( 3 о +3 1 t +3 2 1 ² +3 3 1 ³ ) +

• ⁺ P 1 ( ³ 6 ⁺³ 7 t ^{+ 3} 8 t ^{2 +3} 9 ■ t ³ ) ⁺

• ⁺ P 2 ( ³ 12 ^{+ 3} 13 t ^{+ 3} 14 t 2 ^{+ 3} 15 t 3 ) ⁺

• ^{+ p} 3 ( ³ 18 ^{+ 3} 19 t ^{+ 3} 20 t ^{2 + 3} 21 t 3 ) ⁺

• ⁺ P ⁴ ( ³ 24 ⁺³ 25 t ^{+ 3} 26 t ^{2 + 3} 27 t 3 ) •                ⁽³⁾

Для кластера С методом срезов в рамках модели (1) не найдено удовлетворительных математических моделей.

Метод уточнения вида моделей ФП

Метод всех возможных регрессий [5] позволяет уточнить математическую модель, найденную методом срезов, путем исключения из нее избыточных коэффициентов, которые ухудшают качество модели при проведении процедуры верификации.

Суть метода всех возможных регрессий заключается в переборе всех вариантов математических моделей, которые могут быть получены из слагаемых предварительно сформированной математической модели. Каждая математическая модель оценивается с точки зрения удовлетворения предельно допустимым значениям температурной, приведенной и погрешности от нелинейности. Те модели, которые удовлетворяют этим предельно допустимым значениям, признаются годными для дальнейшего исследования.

При проведении исследований методом всех возможных регрессий партии ИП [1] были приняты следующие уровни максимально допустимых погрешностей:

• 1)    максимальная приведенная погрешность γ = 0,075 %;

• 2)    максимальная погрешность от нелинейности γ нел = 0,060 %;

• 3)    максимальная температурная погрешность γ темп = 0,080 %.

Применение метода всех возможных регрессий связано с большим объемом вычислений и большим количеством моделей, удовлетворяющих приведенным выше максимально допустимым значениям погрешностей. Для обоснованного выбора одной модели из множества полученных в статье предлагается оценивать сложность найденных математических моделей и выбирать модели, имеющие низкие показатели сложности.

Математические модели функций преобразования для системы кластеров измерительных преобразователей давления

Оценка сложности математических моделей

Для оценки сложности математических моделей предлагается применить метод весового ранжирования коэффициентов модели [6]. Для этого коэффициенты модели (1) группируются следующим образом:

P = ( Р з5 t 5 p 5 ) +

+ ( ₽ 29 t 5 p ^{4 +} Р з4 t 4 p 5 ) ⁺

+ ( P 23 t 5 P 3 +P 28 t⁴P 4 +Р 33 t 3 ) ⁺

+ ( P 17 1 5 P 2 + P 22 1 4 P 3 + P 27 1 3 P 4 + Р 32 1 2 P 5 ) +

+ ( P 11 1 5 P 1 + P 16 1⁴P 2 + P 21 1 3 P 3 + P 26 1 2 P 4 + Р 31 tP 5 ) +

+ ( P 10 1 4 P 1 + P 15 1 3 P 2 + P 20 1 2 P 3 + P 25 1 1 P 4 ) +

+ ( P ₉ t ³ P ¹ +P j4 t 2 P 2 +P ₁₉ t ¹ P 3 ) +

+ ( P ₈ t 2 P ¹ +P 13 t ¹ P 2 ) ⁺

⁺ ( p 7 t ^P ) +

+ ( p 5 1 5 +P 4 t ⁴ +P 3 1 3 + P 2 1 2 +P 1 1 ¹ ) +

+ ( p 30 P 5 + P 24 P ⁴ + P 1 ₈ P ³ +P 12 P ² +p ₆ P ¹ ) + ( P e ) . (4)

Показатель сложности математической модели представляется 36-разрядным двоичным числом. В определенном разряде находится 0, если данный коэффициент не присутствует в модели, и 1 – если присутствует. Самому старшему разряду соответствует коэффициент P ₃₅, а самому младшему - Р ₀ (см. выражение (4)). Переводя полученное число в десятичное, получаем значение показателя сложности модели ФП измерительного преобразователя давления.

Достоинство данного метода состоит в том, что с его помощью можно оценить сложность всего множества частных моделей в рамках общей модели (1).

Таблица 1

Математические модели для кластера А

№ модели	Маска модели	Сложность модели	Приведенная погрешность, %
			min	сред.	max
1	111100110100111100110000000000000000	645583	0,00005	0,00604	0,02744
2	111100111100111100110000000000000000	653775	0,00002	0,00450	0,01733
3	111100111100110100111000000000000000	883151	0,00011	0,00453	0,01622
4	111100110100111100111000000000000000	907727	0,00003	0,00583	0,02761
5	111100111100101100111000000000000000	911823	0,00002	0,00501	0,01864
6	111100111100111100111000000000000000	915919	0,00002	0,00451	0,01745
7	111100111100111000111100000000000000	8780239	0,00004	0,00452	0,01752
8	111100111100110100110100000000000000	9009615	0,00005	0,00458	0,01731
9	111100110100111100110100000000000000	9034191	0,00004	0,00604	0,02744
10	111100111100101100110100000000000000	9038287	0,00015	0,00558	0,01985
11	111100111100111100110100000000000000	9042383	0,00002	0,00451	0,01751
12	111100111000111100111100000000000000	9238991	0,00022	0,00468	0,01777
13	111100111100110100111100000000000000	9271759	0,00001	0,00452	0,01753
14	111100111100101100101100000000000000	9284047	0,00004	0,00468	0,01704
15	111100111100111100101100000000000000	9288143	0,00004	0,00467	0,01702
16	111100110100111100111100000000000000	9296335	0,00002	0,00487	0,01760
17	111100111100101100111100000000000000	9300431	0,00003	0,00468	0,01710
Максимально допустимые значения, %			0,075

Таблица 2

Математические модели для кластера В

№ модели	Маска модели	Сложность модели	Приведенная погрешность, %
			min	сред.	max
1	111100111100111100111100101000000000	9302363	0,00016	0,010	0,044
2	111100111100111100111100111000000000	13627739	0,00001	0,010	0,034
3	111100111100111100111000101100000000	135131483	0,00012	0,010	0,043
4	111100111100111100111100100100000000	143520091	0,00004	0,010	0,044
5	111100111100111100111100101100000000	143520091	0,00037	0,010	0,043
6	111100111100111100111100101100000000	143520095	0,00027	0,010	0,035
7	111100111100111100101100111100000000	147829087	0,00000	0,012	0,043
8	111100111100111100111100110100000000	147845467	0,00008	0,010	0,037

Метрологический запас по приведенной погрешности моделей ФП

Таблица 3

Метрологический запас		K м.з (min)	K м.з (сред.)	K м.з (max)
Кластер А	Модель (5)	3,9	7,5	15,0
	Стандартная	2,1	3,2	5,0
Кластер В	Модель (6)	4,4	8,9	15,0
	Стандартная	1,5	2,0	2,5

Результаты исследований

Применение метода всех возможных регрессий позволило уточнить предварительно сформированные методом срезов математические модели функции преобразования измерительных преобразователей давления для кластеров А и В. Найденные модели и их показатели сложности представлены в табл. 1 и 2.

Для ИП кластера А предлагается использовать модель вида

P = p 0 ( в о + 0 1 1 + 0 2 1 ² + 0 3 1 ³ ) +

^{+ p} 1 ( ⁰ 6 ^{+ 0} 7 t ^{+ 0} 8 ' t 2 ⁺ 0 9 t 3 ) ⁺

^{+ p} 2 ( ⁰ 12 ⁺⁰ 13 t ^{+ 0} 14 t 2 ) ⁺

+ p ³ ( 0 ₁₈ +0 ₁₉ 1 + 0 20 1 ² +0 21 t ³ ) .                (5)

Для ИП кластера В предлагается использовать модель вида

P = p ⁰ ( 0 0 +0 1 1 + 0 2 1 ² + 0 3 1 ³ ) +

^{+ p} 1 ( ⁰ 6 ⁺⁰ 7 t ^{+ 0} 8 t 2 ⁰ 9 t 3 ) ⁺

^{+ p} 2 ( ⁰ 12 ^{+ 0} 13 t ^{+ 0} 14 t 2 ^{+ 0} 15 t 3 ) ⁺

^{+ p} 3 ( ⁰ 18 ^{+ 0} 19 t ^{+ 0} 2O t 2 ^{+ 0} 21 t 3 ) ⁺

+ p ⁴ ( 0 24 +0 25 1 + 0 2 ₆ 1 2 ) .                        (6)

Минимальное, среднее и максимальное значения метрологического запаса по приведенной погрешности для моделей (5) и (6) в сравнении со стандартной моделью, применяемой в настоящее время, показаны в табл. 3.

Под метрологическим запасом нами понималось следующее выражение

K м.з = 0,075/ Y ,                               (7)

где 0,075 – максимально допустимая приведенная погрешность для исследованных преобразователей давления, %; γ – максимальная приведенная погрешность для конкретного измерительного преобразователя найденная по результатам испытаний ИП, %.

Заключение

Предлагаемая поэтапная процедура формирования математической модели функции преобразования для ИП кластеров А и В позволяет увеличить метрологический запас измерительных преобразователей по приведенной погрешности за счет учета индивидуальных особенностей кластеров.

Найденные математические модели (5) и (6) позволяют увеличить средний метрологический запас по приведенной погрешности для кластера А в 2,3 раза, а для кластера В – в 4,5 раза по сравнению со средним запасом, обеспечиваемым на современном этапе производства, что может способствовать увеличению межповерочного интервала измерительных преобразователей давления.