Математические модели и программные средства оценки напряженно-деформированного состояния литосферы земли

Современные геодеформационные процессы, связанные с деформациями, возникающими при движениях отдельных слоев и блоков литосферы на различных глубинах, в том числе и на дневной поверхности литосферы, согласно документально подтвержденным фактическим данным, представляют собой фактор риска возникновения чрезвычайных ситуаций геодинамического характера. Для изучения причин таких движений и деформаций необходимы исследования пространственно-временной динамики современных литосферных геодеформационных процессов.

Преимущество метода математического моделирования перед другими методами исследования геодеформаци-онных процессов является значительным [1–2], особенно если этот метод применяется в рамках комплексного подхода при оценке риска чрезвычайных ситуаций геодинамического характера [1]. Важную роль играют экономическая эффективность, оперативность и быстроокупаемость этого метода. Кроме того, метод математического моделирования позволяет достаточно легко менять объект исследования.

Все действия по обработке и интерпретации исходной информации, получению и анализу результатов исследований, а также по оценке развития геодинамической ситуации выполняются с помощью средств компьютерной техники, что и обеспечивает высокоэффективное и быстрое решение поставленных задач.

Существующие математические модели и методы восстановления полей геодинамических напряжений и смещений, технологии выявления потенциально опасных в сейсмическом отношении территорий разработаны для ряда различных регионов и разнообразных по своему назначению объектов.

Задачи же по глобальному моделированию современных литосферных геодеформационных процессов, их про- странственно-временной динамике еще полностью не решены, что требует разработки соответствующих математических моделей и методов.

В связи с этим данная статья посвящена построению глобальной математической модели при оценках напряженно-деформированного состояния литосферы Земли.

Полученные результаты могут быть использованы для создания оценочнопрогностических карт эквипотенциального распределения сдвиговых упруговязких деформаций в литосфере.

Вертикальные и горизонтальные движения отдельных слоев и блоков земной коры характеризуются следующим набором параметров:

• 1)    вертикальные и горизонтальные смещения в геологической среде;

• 2)    скорости вертикальных и горизонтальных движений в геологической среде;

• 3)    напряжения и деформации в геологической среде, возникающие вследствие осуществления вертикальных и горизонтальных движений;

• 4)    относительная плотность потенциальной энергии деформируемых пород геологической среды;

• 5)    плотность геологической среды;

• 6)    упругие модули геологической среды;

• 7)    вязкость геологической среды;

• 8)    ускорение свободного падения.

Поскольку в сферу наших интересов попадают именно литосферные гео-деформационные процессы, т. е. процессы, формирующиеся и протекающие в литосфере, то мантийные воздействия учитываются опосредованно, на основании учета влияния изостатических аномалий гравитационного поля. Именно поэтому за нижнюю границу модели литосферы принят глубинный уровень в 80 км, т. е. толщина представленной модели может составлять 80 км.

Обзор литературы

При изучении зарубежной литературы по данной тематике было выявле- но, что оценка рисков в сложных распределенных природно-технических системах не осуществляется посредством математического моделирования, а реализуется с помощью приборных исследований, основанных на системах глобального позиционирования GPS. Таким образом, в зарубежных литературных источниках отсутствуют аналоги описанным в данной статье методам.

Приведем обзор существующих на сегодняшний день математических моделей и комплексов программ по оценке напряженно-деформированного состояния поверхности Земли.

По видовому признаку математические модели исследования литосферных геодеформационных процессов подразделяются на детерминированные, вероятностные модели, и модели, использующие в своей основе методы теории нечетких множеств.

Детерминированные модели по своему пространственному разрешению бывают либо двумерные, либо трехмерные. Двумерные модели позволяют решать ограниченный круг практических задач, обычно связанных с оценкой гео-динамического риска вдоль какого-либо профильного направления, т. е. в вертикальных разрезах земной коры. В настоящее время подобные модели практически не используются, и основное внимание в оценках геодинамического риска уделяется трехмерным моделям. Они более эффективны, поскольку позволяют охватывать уже не отдельные слои, а целые блоки земной коры. Трехмерные модели, как правило, содержат граничные условия следующего вида [3; 4]:

' р gu z ⁽x , y , h) ^- ^ ( x , y , h) = 0,

_ " . (x , y ,0) + ( р 0 - р ) gU z ( x , y ,0) = p h max P(x , У ), T xz ⁽ x , y , h ) = ⁰,

_ Txz (x, y ,0) = 0, где Txz- касательные напряжения в плоскости XZ; oz - вертикальная составляющая нормальных напряжений; uz – вертикальная составляющая полного вектора смещений в геологической среде; P(x, y) – величина распределенной нагрузки в точке с координатами (x, y); р - средняя плотность вещества геологической среды; ρ0 - средняя плотность вещества ниже условной модельной границы приложения внешней распределенной нагрузки; g – ускорение силы тяжести; hmax – наибольшая величина отклонения модельной нижней границы от нулевого уровня; h - средняя толщина рассматриваемого модельного упругого пространства.

Аналитические выражения для компонент тензора напряжений и составляющих вектора смещений в геологической среде в обобщенном виде в таких моделях обычно записываются в следующем виде [3; 4]:

s

■ (х, y, z)=1 от+1 е -am0) + 42

l

+ 1 е -а^о n )

² n =1

sl

+ ЕЕ О а mn\

U b ( x , У , z ) =   u b ’ + E u b +

• ^{4         2} m =1

lsl

+1E ub0 n) +EE ubmn),

² n =1            m =1 n =1

где a G { x , y , z , xy , xz , yz } , b G { x , y , z } .

Трехмерные модели с граничными условиями (1) используются исключительно при оценках сейсмического риска для территорий регионального масштаба, т. е. для достаточно обширных районов земного шара.

Для количественной оценки сейсмической опасности на региональном масштабном уровне существует компьютерная программа GeoTens [4; 5].

Компьютерная программа GeoVector позволяет численно реализовать вертикально-горизонтальную математическую модель оценки геодинамической устойчивости среды распределенной природно-технической системы [4; 5].

Информатика, вычислительная техника и управление

В программе GeoVector имеется возможность учета сброса напряжений (рассеяния сейсмодеформационной энергии) посредством задания условия в окне «Сброс напряжений».

Основополагающим принципом при построении вероятностных моделей является предположение о том, что последовательность геодинамических состояний геологической среды исследуемой территории представляет собой поток однородных событий, удовлетворяющий также условиям независимости, однородности и ординарности, т. е. представляет собой так называемый простейший поток [4].

Недостаток вероятностных моделей заключается в том, что их использование, как и использование детерминированных моделей, на неоднородных в геологическом и тектоническом отношении территориях не всегда позволяет адекватно выполнить оценки геодинамического риска. Это относится и к территориям, где имеется существенная неопределенность в отношении информации о физико-механических характеристиках геологической среды и (или) распределенных геофизических полях-источниках геоди-намических аномалий. Все это послужило веским доводом в пользу того, что были предприняты весьма удачные попытки разработки моделей, основанных на теории нечетких множеств [3; 6].

Как известно, при использовании этой теории в практических целях особенно важно грамотно сформировать базу правил системы нечеткого вывода, выбрать входные и выходные лингвистические переменные [7–10]. Поэтому в работах, посвященных построению моделей, основанных на теории нечетких множеств, в качестве входных переменных используются характеристики геологической среды, полученные как на основании анализа макросейсмиче-ских и других геофизических данных, так и информация о напряжениях, смещениях и деформациях, рассчитанных в результате применения детерминиро- ванных и вероятностных математических моделей. После этого формируется набор выходных переменных, который затем подвергается процедуре фаззифи-кации [6].

В ряде других работ представлены модели нечеткой оценки состояния геологической среды, основанные на прямом нечетком выводе и алгоритме Мамдани, а также модели, использующие алгоритм Сугено [2].

Модели, сконструированные на основе алгоритма Мамдани, позволяют на основе анализа топографического рельефа местности и экспертных оценок физических характеристик геологической среды заблаговременно до начала проведения строительных работ выполнить превентивные оценки гео-динамической устойчивости геологической среды в виде значений геодина-мического риска, что дает возможность произвести предварительную оценку проекта планировочных решений по застройке той или иной территории.

Алгоритм Сугено авторы работ предлагают использовать при построении модели нечеткой оценки состояния геологической среды при наличии воздействия на эту среду статической нагрузки от будущих зданий и сооружений.

Для реализации одной из моделей нечеткой оценки опасных геодина-мических процессов можно воспользоваться компьютерной программой GeoFuzzyCalc, которая дает возможность повышения эффективности оценки гео-динамического риска на платформенных территориях в условиях неопределенности и неоднозначности информации о состоянии геологической среды этих территорий на основе использования нечеткой модели, построенной на базе прямого нечеткого вывода [2].

Описанные программные продукты разработаны в среде программирования Borland Delphi 7.0.

К настоящему моменту времени разработан достаточно разнообразный и широкий спектр математических мо-

[ETS]

делей, алгоритмов и соответствующих им программных средств, позволяющих оценивать многие опасные ге-одеформационные процессы. Однако описанные выше модели не позволяют «отследить» динамику изучаемых гео-деформационных процессов. Поэтому одна из главных задач данного исследования состоит в том, чтобы разработать новые математические модели, позволяющие построить такую количественную модель литосферы, учитывающую комплекс взаимосвязей между отдельными геологическими структурами, которая давала бы в будущем возможность контролировать в режиме реального времени динамику литосферных геодеформационных процессов.

Материалы и методы

Основным фактором, влияющим на формирование и развитие геодина-мических неустойчивостей (т. е. землетрясений), как показывают результаты исследований [11-16], является гравитационное поле планеты. При математическом моделировании напряжений в статье используются данные аномального гравитационного поля в изостатической редукции.

Если подходить к вопросу о построении математической модели напряженно-деформированного состояния литосферы в глобальном масштабе с теоретических позиций, то в первую очередь

Том 29, № 1. 2019

необходим контроль правильности расчета напряжений каким-либо параметром, значения которого в глобальном масштабе известны по данным наблюдений.

В качестве такого параметра авторы предлагают использовать данные о скоростях движений на поверхности земной коры (рис. 1).

Представленная на рис. 1 карта является авторской разработкой ученых Калифорнийского Технологического института, созданной по данным измерений, выполненных группировкой из 30 спутников, входящих в глобальную систему позиционирования ¹ . Эти данные успешно применяются для навигации и точного измерения геодезических координат различных объектов.

Полученные данные о скоростях горизонтальных и вертикальных движений на поверхности земной коры были подвергнуты обработке с целью получения распределения значений скоростей этих движений по равномерной сетке как в долготном, так и в широтном направлениях. Процедура обработки выполнялась на основании метода интерполяции Крайгинга.

На основании метода Крайгинга, реализованного в программном комплексе Surfer 10.0, построено поле распределения векторов скоростей горизонтальных и вертикальных движений на поверхности земной коры.

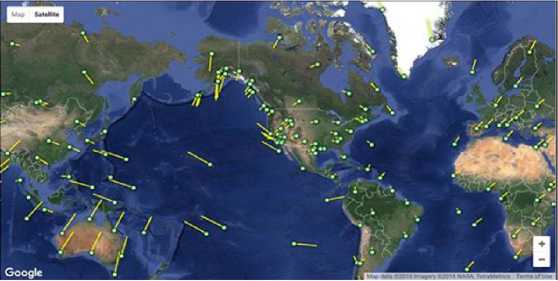
Р и с. 1. Карта скоростей горизонтальных движений на поверхности земной коры (мм/год)

F i g. 1. The map of velocities of horizontal movements on the crustal surface (in mm/year)

Рассмотрим теперь математическую модель напряженно-деформированного состояния литосферы Земли, построенную на основании данных об аномальном гравитационном поле в изостатической редукции и информации о распределении скоростей горизонтальных движений на поверхности земной коры. В математической модели величины гравитационных аномалий измеряются в мГал (миллигалах), скорости движений из мм/год пересчитаны в м/год.

Математически модель напряженно-деформированного состояния литосферы Земли представляет собой следующие системы уравнений:

щина модельного слоя геологической

среды (литосферы); t – временной интервал (1 год); ρ_H ( x , y ) – плотность геологической среды в точке с координатами ( x , y ), вычисляемая по соотно-

шению

H

Г н ( x , У ) = / Г ( x , У , Z)dz .

Для расчета компонент тензора напряжений и составляющих вектора смещений в литосфере достаточно

^ ( x , y ,0) = P h ( x , y ) A g_u ( x , y) xH ( x , y ),

1) U z ( x , y , h) = V z ( x , y , h)t ,                  p^

U x ( x , y , h ) = V x ( x , y , h )t , . - . ( x , y , h ) = 0,

■ Oz (x, y ,0)=Ph (x, y) Agu (x, y) xH (x, y), uz (x, y, h ) = Vz (x, y, h )t, uy (x, y, h)=vy (x, y, h )t, тTyz (x, y, h) = °,

воспользоваться одним из соотношений, поскольку выражения для компонент сдвиговых напряжений и компонент горизонтальной составляющей вектора смещений формально будут одинаковыми, различаясь только координатами x и у . Будем строить выражения для компонент тензора напряжений и составляющих вектора смещений, основываясь на системе уравнений (1) и следующих соотношениях (для k -ой гармоники), общепринятых в литературе, посвященной оценке геодинамиче-ского риска [5; 6; 15]:

^z ( x , У , z ) = k 2 IT -T^- U_ ^ + й

C - k ( B + Dz )

shkz +

где s _z ( x , y, 0) - вертикальная компонента нормальных напряжений на границе «литосфера – литосферная мантия»; U z ( x, y , h ) - вертикальная составляющая вектора смещений на поверхности земной коры; u x ( x , y , h ) - x -компонента горизонтальной составляющей вектора смещений на поверхности земной коры; u y ( x , y , h ) - y-компонента горизонтальной составляющей вектора смещений на поверхности земной коры; t yz ( x , y , h ) - компонента сдвиговых напряжений в плоскости XZ на поверхности земной коры; t yz ( x, y, h ) - компонента сдвиговых напряжений в плоскости YZ на поверхности земной коры; Dg u ( x , У ) - величина аномалии гравитационного поля в изостатической редукции в точке с координатами ( x , y ); H ( x , y ) – толщина литосферы в точке с координатами ( x , y ); c - безразмерный коэффициент, равный 10 6 ; h - тол-

+

й

Л + й

D - k (A + Cz )

k

U z ⁽ x , У , z ) =x-² й

+

<

chkz ^ cos k_xx cos k_yy ,

² й

Л + й

D - k ( A + Cz )

shkz +

2 й

Л + й

C - k ( B + Dz

chkz f cos k x x cos k y y,

k

U x ( x , y , z ) = Tj x {[ k ( B + Dz ) + C ] shkz + ² й

+ [ k ( A + Cz ) + D ] chkz } sin k_x cos k_yy ,

T xz ( x , У , z ) = kk x

k ( A + Cz ) + -^- D Л + й

Г                   1

+ k ( B + Dz ) + _^- L            л + й

shkz +

C chkz ^ sin k x x cos k_yy , (5)

где A , B , C , D - неизвестные коэффициенты, определяемые из условий математической модели (3).

Подставляя уравнения (5) в соответствующие соотношения системы (3) и выполнив необходимые преобразования, получим следующую систему уравнений:

удобства расчетов обозначение

P g ( x , У ) = P h ( x , У )A g u ( x , У ) x H ( x , У ) , получим следующую систему уравнений:

^{k 2} 1 T^{- D -} kA I = P h ^{( x} ’ У ^{) A g} u ⁽ x ’ У ) X ^{H (} x , y)’ V X + -     )

-У— D + P g ⁽ x ’ y ) - Ckh ) shkh +

X + ц       k ²          у

+

C - kB - Dkh I chkh _ 2 ^z ⁽ x , y , h ) t

k

, 2^-D - k ( A + Ch ) shkh +

2 -+-          J

+ X^- C - k ( B + Dh ) chkh U v ( x , y , h ) t ,

X + -            J ^z

z

k^ - { [ k ( B + Dh ) + C ] shkh +

2 -

+ [ k ( A + Ch ) + D ] chkh } = v_x ( x , y , h ) t ,

k ( A + Ch ) +— D shkh +

_           X + - _

+ k ( B + Dh ) +— C chkh = 0.

_            X + - _

¹ (6)

Выражая из первого уравнения системы (6) неизвестный коэффициент A , получим:

A =-- ^ц--D k ( X + ц )

—

P h ( x , У ) A g u ( x , y ) x H ( x , y )

k ³

,

k

,

^{2 ц} D — kA — Ckh shkh +

_ X + ц               _

+

2 ц

_ X + ц

C — kB — Dkh I chkh = ^{2 ц} ^ ⁽ x ^{, y}, h)t

k

,

( kB + Dkh + C ) shkh +

+ [ D ^Г+ 1 1- P g ⁽ x ^, y ) + Ckh I chkh _

LI X + ц У k ²        J

_ 2 p v x ( x , y , h ) t

k x

P g ( x , У ) k ²

,

+ Ckh I shkh +

Г              X

+1 kB + Dkh +-- C I chkh _ 0.

у            X + Ц у

Выразим из третьего уравнения системы (8) коэффициент B , а именно:

B = Pg (x,y) th(kh) — [kh + th(kh)]d — k3

—

+ khth ( kh ) | C .

A + ц          )

(kB + Dkh + C) shkh + (kA + Ckh + D )chkh = = 2цvx(x, y, h)t kx        ,

Подставив выражение для коэффициента B в первое и второе уравнения системы (9) и выполнив необходимые преобразования, получим систему, состоящую из двух уравнений:

C + Dth(kh) _ 2^(A + ^)Vz (x,y,h), k (A + 2 ^)     ,

^{А + 2 ц} ch ( kh) - th ( kh) - sh ( kh ) I D +

A + ^                     J

| kA + Ckh + — ^X— D | shkh + у            X + ц у

+1 kB + Dkh + ^X C I chkh = 0. V            ^x + ц у

Подставляя выражение для коэффициента A в остальные урав-

нения системы (7) и вводя

для

+( kh - ch(kh) + — ^— sh(kh) -

+

kh - th(kh ) - sh(kh ) ) ( kh - ch(kh ) +

-У— sh ( kh ) - kh - th ( kh ) - sh ( kh))C _

_ 2 ^V x ( x , y , h) + P g ( x, y )

k x

k2

X

x[ch ( kh) - th(kh) - sh ( kh )].

Информатика, вычислительная техника и управление

Получим теперь из первого уравнения системы (10) соотношение для коэффициента C :

O x ( x , y , z )

= \W ( B + Dz ) + C [ k x + ^A k [                  I      A + p _г

shkz +

+

C = 2 м ( А + м ) v z ( x , y , h ) - D . th ( kh) q ^ k ( А + 2 м )              ( ) ( )

kk x ( A + Cz ) + D [ k x + 2k— ] .                    [ ^A + д J.

x cos k x x cos k y y,

chkz

x

(13.2)

С учетом соотношения (11) второе уравнение системы (10) теперь будет содержать только один неизвестный коэффициент D . В таком случае приведем теперь окончательное выражение для нахождения коэффициента D :

D = f 2 ц У х ( x , y , h ) +

V      k_x

+ P g ⁽ x ’ y ) [ch ( k h ) - th ( kh ) ■ sh ( kh )] - k

• - 2 ц ^{( А} + ц ) V z ⁽ x , y , h )

k (A + 2 ц)     J x | kh ■ ch( kh) +—ц— sh(kh) -

V            A + ц

(- kh ■ th (kh) ■ sh(kh))/ А+2ц x x               7 A + ц

x [ ch ( kh ) - th ( kh ) ■ sh ( kh )] +

+ kh ■ sh(kh ) ^f shkh ) ■ th ( kh ) - 1 ) . (12)

V ch ( kh )            J

Таким образом, используя соотношения (9), (11), (12) и первое уравнение из системы (7), можно рассчитать компоненты S z, ( x , y , z ), t xz ( x, y, z ) тензора напряжений и составляющие u_z ( x , y , z ) и u_x ( x , y , z ) вектора смещений в литосфере, представленные в системе (3).

Приведем также выражения для u_y ( x, y, z ) - составляющей вектора смещений и остальных компонент тензора напряжений [4; 5; 15; 16]:

k

U y ( x , y , z ) = -{ {[ k ( B + Dz ) + C ] shkz + 2 ц

+ [ k ( A + Cz ) + D ] chkz } cos k x x sin k y y, (13.1)

f[                        f         Ук¹ 1

a y ( x , y , z ) = \ kk² y (B + Dz ) + C k y ² + ^^ shkz +

11                 I A + д Л

+ kk y (A + Cz ) + Dk y + 2 ^13 chkz I x

I A+дЛ I xcos kxx cos kyy,          (13.3)

T yz ( x , y , z ) = kk y

k (A + Cz) +     D

A + ^ .

shkz +

A k (B + Dz ) +-- C

A + ^

chkz I x

x cos k x x sin k y y ,            (13.4)

txy(x, y, z) = -kxky {[k(B + Dz) + C] shkz + + [ k (A + Cz) + D ] chkz }x x sin kxx sin kyy. (13.5)

Используя соотношения (13.1)– (13.5) и выражения системы (5), мы можем восстановить во всем объеме литосферы поля напряжений и смещений, соответствующие упругой модели, учитывающей пространственные вариации упругих модулей, поскольку величины λ и µ входят в выражения для компонент тензора напряжений и составляющих вектора смещений.

Однако нас интересует не теоретическое пространственное распределение напряжений, смещений и деформаций в литосфере Земли, а распределение, соответствующее реальной геологической среде, состояние которой в значительной степени зависит от пространственного распределения температуры в литосфере и, как следствие, от пространственной вариативности вязкости геологической среды.

Для оценки пространственной вариативности вязкости геологической среды в зависимости от пространственного распределения температуры в литосфере Земли была использована методика определения величины вязкости, основанная на достаточно хорошо известном соотношении, связывающим вязкость, температуру, упругие модули и энергию активации ² [1]:

, s ,       Ua     ( 2.5P И п(г) = A exp \т exp I    2J|, (14)

где R - газовая постоянная, равная 8,31 —^^—; T — температура; P -,    моль -° К давление; Ua – энергия активации; Ak – некоторый коэффициент пропорциональности.

Численные значения всех величин, входящих в данное соотношение, были либо определены нами ранее, либо заимствованы из работ других авторов ³ ; ⁴ [1–4; 17].

Согласно упруго-вязкой модели Максвелла, общая деформация складывается из упругой и вязкой состав-ляющих ^{5; 6} [17; 18]:

PP

Y = - + ■ т ,       (15)

Eη где g – деформация; P – напряжение;

^{(3 А} + 2 ц ) ц

E =--упругий модуль (мо

А + ц дуль Юнга); h - вязкость; t - время.

В таком случае можно рассчитать деформации (особенно сдвиговые), которые ответственны за формирование и реализацию опасных литосфер-

ных геодеформационных процессов по упругой и упруго-вязким моделям, и затем сопоставить полученные результаты расчетов, используя для оценки достоверности данных моделей распределения эпицентров уже произошедших сейсмических событий на различных глубинных уровнях.

Результаты исследования

На основании соотношений (5), (13.1)–(13.5) и с учетом выражения (14) произведен расчет напряженно-деформированного состояния литосферы Земли на различных глубинных уровнях по упругой и упруго-вязким моделям.

Численные расчеты напряжений, смещений и деформаций в литосфере Земли были выполнены с помощью компьютерной программы GeoTens (рис. 2).

После запуска программа запрашивает имя файла изостатических аномалий, которое нужно обязательно ввести, поскольку именно в этом файле в формате системы GEOGRID размещена информация о внешней вертикальной нагрузке, действующей на среду РПТС. Также необходимо ввести глубины (в км), на которых расположены условная граница возмущений и расчетная плоскость. После ввода с клавиатуры длин (в км) долготного и широтного профилей необходимо нажать на кнопку «Прочитать». При этом происходит считывание данных из файла изостатических аномалий, и программа готова к выполнению расчетов. Расчеты производятся после нажатия на кнопку «Рассчитать».

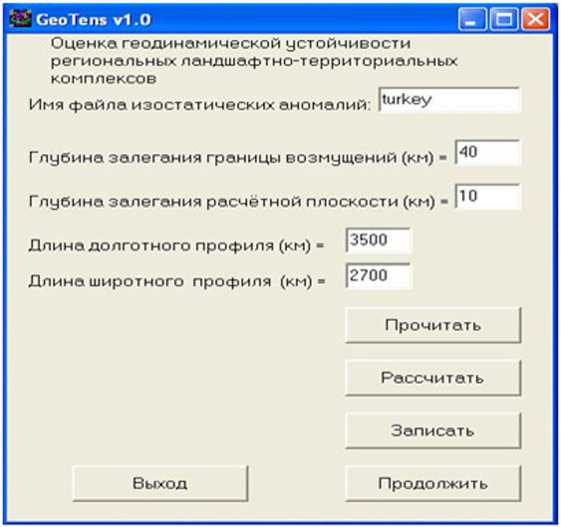
Р и с. 2. Рабочее окно программы GeoTens

F i g. 2. Working window of the GeoTens program

После этого необходимо записать полученные результаты во внешние файлы (по каждой компоненте тензора напряжений и составляющей вектора смещений в геосреде записывается отдельный файл), нажав на кнопку «Записать». Далее можно продолжить расчеты по какой-либо другой территории (нажав на кнопку «Продолжить»), либо выйти из программы (кнопка «Выход»).

Полученные результаты исследований с помощью программного комплекса Surfer в виде изолиний выводятся на карты и представлены на рис. 3; 4.

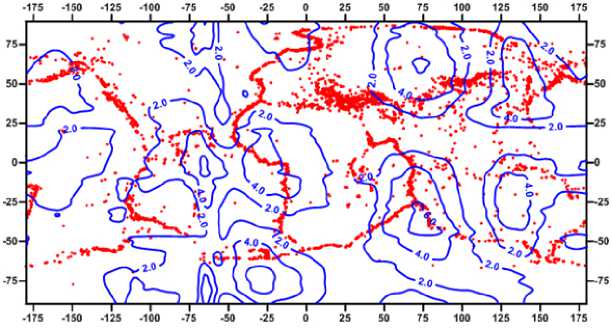
Р и с. 3. Эквипотенциальное распределение сдвиговых упругих деформаций в литосфере на глубине 10 км (сечение изолиний 2 · 10^‒8), осредненных за 1 год. Кружками красного цвета изображено распределение эпицентров сейсмических событий на глубине 10 км за период времени 1914–2014 гг. (карта построена авторами)

F i g. 3. The equipotential distribution of the shear elastic deformations in the lithosphere at a depth of 10 km (the section of the isolines is 2 • 10^-8) averaged over 1 year. Mugs of red color depict the distribution of epicenters of seismic events at a depth of 10 km for the period of 1914-2014 (the map was built by the authors)

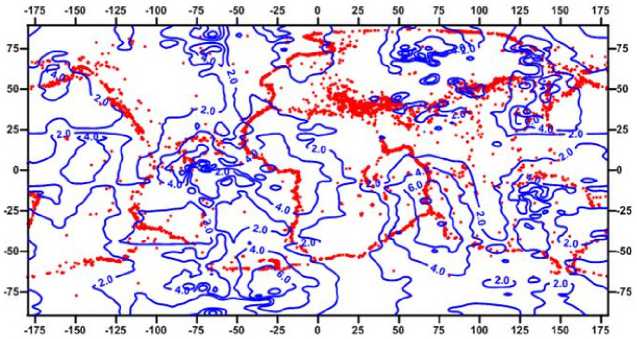
Р и с. 4. Эквипотенциальное распределение сдвиговых упруго-вязких деформаций в литосфере на глубине 10 км (сечение изолиний 2 • 10 8 ), осредненных за 1 год (карта построена авторами)

F i g. 4. The equipotential distribution of the shear elastic-viscous deformations in the lithosphere at a depth of 10 km (the section of the isolines is 2 • 10 8 ) averaged over 1 year

(the map was built by the authors)

62                                    Информатика, вычислительная техника и управление

Обсуждение и заключение

В статье предложена новая глобальная математическая модель оценки напряженно-деформированного состояния литосферы Земли. Представленную модель можно использовать для оценки как упругих, так и упруго-вязких деформаций; при этом, как показали численные расчеты, упруго-вязкая модель имеет более высокую коррели-рованность распределений эпицентров сейсмических событий и сдвиговых деформаций, чем упругая модель. Кроме того, информация по упруго-вязким сдвиговым деформациям позволяет перейти к оценке упруго-вязких сдвиговых напряжений, что, с учетом выполненных численных расчетов характеристик современных литосферных геодеформационных процессов, является существенным вкладом в решение проблемы обеспечения безопасности территорий от проявления опасных эндогенных геологических процессов.

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.