Математические модели и решение задачи сейсмодинамики подземных трубопроводов

В статье проанализированы отечественные и зарубежные работы, в частности, материалы XIV (Пекин, 2008) и XV (Лиссабон, 2012) Всемирных конференций по сейсмостойкому строительству и Международной конференции по проектированию в геотехнической инженерии (Токио, 2009), связанные с исследованием систем жизнеобеспечения типа подземных газо-, водо- и нефтепроводов, с целью дополнить разработанную теорию новыми данными, оценить ее результативность и установить уровень настоящей работы.

Современное состояние вычислительных средств позволяет более полно учесть многочисленные факторы и с большей степенью достоверности определить фактическое напряженно-деформированное состояние подземного трубопровода.

Данная статья посвящена исследованию сейсмодинамики подземных трубопроводов на основе сейсмодинамической теории подземных сооружений [1] с привлечением математической модели теории стержней, рассмотренных в работе [3] для случая перемещения точек стержня при совместном действии продольных и поперечных сил. Выведена система уравнений движения линейного подземного трубопровода на основе вариационного принципа Гамильтона - Остроградского при произвольном направлении сейсмической волны относительно оси трубопровода.

Математические модели

Для изучения совместных продольных, поперечных колебаний подземных сооружений типа трубопроводов при произвольном направлении сейсмического нагружения применим прикладную теорию колебаний стержней.

На основе допущений, приведенных в работе [3], трубопровод моделируется в виде стержня (рис. 1), α – угол падения сейсмической волны, а перемещения выбираются следующим образом:

u 1 = u - y a 1 , и 2 = v , (1)

где и 1 , и 2 - перемещения точки трубопровода, и - продольные перемещения, v - поперечное перемещение, а 1 - угол поворота сечения трубы.

Для вывода дифференциальных уравнений с граничными и начальными условиями используем вариационный принцип Гамильтона – Остроградского

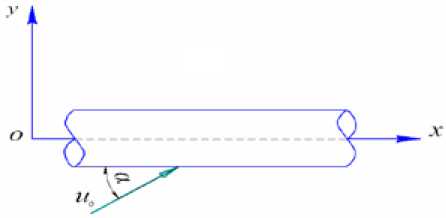
Рис. 1. Схема подземного трубопровода при произвольном направлении сейсмического воздействия на горизонтальной плоскости

J(8T-8П + 8A> = 0,                                              (2)

t где Т – кинетическая энергия, П – потенциальная энергия, А – работа внешних сил, t – время.

При этом вариации кинетической, потенциальной и работы внешних сил представлены в виде

J 8 T dt = JJ t         tV

d u_x „ 9щ     9 u₂ „ 9u₂

p—18—1 + p—2 8—2 dVdt, 9t   9t      d191

JЗЛdt-JJ(an8n + CT128S12dVdt,(4)

ttV

J 8Adt - J J [P18u 1 + P28u2 ]dVdt + J J [q18u1 + q28u2 dSdt + t         tV                          tS(5)

+ JJ ^A + ф ₂ 8 и ₂ dS 1 dt\ x .

t S 1

Соотношения Коши с учетом формул (1) получают вид

^n

dux d , \ —1 - — (u - ya1), dx dx

^£ 12

du2 d u, - —2 + —1 -

dx

d y    d x

— а.

На вариации потенциальной энергии (4) подставляем выражения соотношении Коши (6). Выделим интегралы по сечениям трубопровода в выражениях вариации кинетической (3), потенциальной энергии (4) и работы внешних сил (5). Выводим соответствующие обозначения. После этого в вариациях кинетической и потенциальной энергий выполним операции интегрирования по частям. Полученные результаты вариации кинетической, потенциальной энергии и работы внешних сил подставляем на вариационный принцип Га мильтона - Остроградского (2). В результате получим следующее вариационное уравнение:

J ( 8 T — 8 П + 8 А ) dt - JJ

t

tx

—

d u  d^Nт a pF —t + —x + Nx (P) + N (q\) 8u + — pIz —y- dt2 dx x 1 x 1               z dt2

д ² а 1

d t

—

5 M + Q„ —⁽ M z ( P ) + M z ( , 1 ) ) 1 ⁸» 1 +— p F d^ ₊

d^ +^^ + _Q„( P 2) + ₀2 ( q 2 ) 8 V . 1 dxd. + d t^{2      d} x                               I

+ J

t

—

M z ( ф 1 )) 8а_х + ( — Q _X2 + Q ₁₂ ( ф ₂ )) 8 , ] x dt + J p F d u 8 u + x L ^д t

да d v

+ pI_z —¹ 8a_x + pF—8 v dx - 0. z d t     ¹ d t

t

Вариации неизвестных функций u , a_t, v не равняются нулю. Поэтому в вариационном уравнении (7) коэффициенты вариации функции u i должны равняться нулю. Таким образом, из вариационного уравнения (7) получаем следующую систему уравнений с соответствующими граничными и начальными условиями:

- ^p F d u + ^N ⁺ N x (P 1 ) ⁺ N x (q i ) = 0,

В²a_x  В M z

)-pIz    -— + Q12-(Mz (Pi)+ Mz (qi))-0,(8)

В t2

- pF+ ^ + Q12(P2) + Qi2(q2) - 0, 512оx естественные граничные условия

(- Nx + Nx(^ M = 0, (Mz - Mz (^ ^ = 0, (- Q12 + Q12 fo ))г^х = 0, (9) xxx естественные начальные условия

„ В u „ p F — 3 u

В t

d a

= 0, pL —^L 3a z В t      ¹

t

= 0, p F—3v = 0. В t    _t

Принимаем, что трубопровод деформируется в пределах упругости. Поэтому для материала трубопровода рассматриваем закон Гука

„    „ В u d8(     ( 48 u 8a_x I

_n = E e 1 1 = E —¹ = E—(u - y a 1 ) = E I-- y —¹ I , Вx    Вx            ( 5 x    Вx J

^ 12

= ^{G e} 12

_ (8 u 2 . 8 u 1 I     8 v

= G I--1--I = G--G a ,

( В x    В z J    В x

где ρ – плотность материала трубопровода, x , y – координата трубопровода, σ 11 , σ 12 – соответственно нормальное и касательное напряжения, ε₁₁, ε₁₂ – продольная и касательная деформации, P 1 , P 2 – объемные силы, q 1 , q 2 – поверхностные силы, φ 11 , φ 12 – торцевые силы, воздействующие на трубопровод.

Используя закона Гука (11), формируем внутренние усилия и моменты трубопровода:

N

x

F

'^F = ^EF l x'

M

^Q 12

(                    u 2 daa

= J y ^ 11 ^dF = j E I y —^{( u -} y « 1 ) d^F = J E l y-— y — I ^dF =^- EI z — ’ ⁽¹²⁾

FFF г          г Г Sv

= f a ₁₂ dF = f G l^ v - a 1 I dF = GF ^ v - GF a 1 .

F        f (дx    JВ

Если подставить выражения внутренних усилий и момента (12) в систему уравнения (8) и граничные условия (9), то уравнения (8) и граничные условия (9) в перемещениях имеют вид

27V

- p F ^ 4 + EF ^ 4 + N ( P ) + N ( q_x ) = 0,

2              2 x 1 x 1

da    da ^^S v

' - pIz ~—^T + EIz "BTT + GF T--GFa1 -(Mz (P1) + Mz (q1))= 0’

• dS2dxx

• - p F   + GF fy - GF ^ a + Q 12 ( P 2 ) + Q 12 ( q 2 ) = 0,

В t2       Вx2

естественные граничные условия примут вид ди

EF+ N (^) 1^и = 0, дx    Л’   .

x

<

да z дx

M z fo

x 0

ai 1 + Q12(Ф2)bv = 0,

x естественные начальные условия примут вид д и

д v

дия        да д v^

p F ^^ = 0, P I z     ^5а i = 0, p F ka^{5 v} = ^{0 д} t _t             ^д t

д t

t

д t

t

Силы взаимодействия трубопровода с грунтом определяются из эксперимента [1, 2, 4]

N x ( q i ) = -п О н к х ( u - u 0 x ) ,

&< q , ) =^- 2(1 ⁺ »„„ W, (V, ^- и „ , ),

M z ( q i ) =      5      ⁽¹ R H k x (« 1 -^ ¹ ,

^(1 + ^ грунт R DH ) I     dx )

где ^ грунт — коэффициент Пуассона грунта, k x - коэффициент продольного взаимодействия с грун-

том, l – длина, D H – наружный диаметр трубы, D B – внутренний диаметр трубы, R H – наружный

радиус трубы, u ox и u_oy - проекции на оси координат закона движения грунта, в = I 1

D

—

B

D H

[1, 2,

• 4] . N x ( P 1 ), M z ( P 1 ), Q 12 < P 2 ), N x (Ф 1 ), M z ( Ф 1 ) и Q 12 < Ф 2 ) при решении данной задачи не учитываются. Если учесть соотношения (16) – (18), то система уравнений (13) получает вид

д ² и       д ² и / _х

- p F —г + EF — -~ n D_Hk_x ( u - u ₀ x ) = 0, d t ²         d x ²

<

-

_pI⁸!oi ₊ EI ⁸!oi ₊ GF ^dv -5 t ²          5 x ²         В x

GF a _x

1 (1 +^ -; ;^ [ dh; )

R H k x \ a _x

1 = 0, 8 x )

- p F ^4 + GF^ - GF ^{d a} 1 - 2(1 + a_p ) nD_Hk_x ( v - u₀ ) = 0. d t ²        d x ²         8 x            ^р               y

Предварительно вводим следующие векторы:

( u

V =

av)

. V 0 =

kF

I ^{u 0} y )

При этом систему дифференциальных уравнений (19), граничные и начальные условия (14) и (15) можно представить в векторной форме ы 82 V    82 V в8 V

M 2 + A 2 + B — + C (V - V0 )= 0, 8t      8x естественные граничные условия (14)

— 8V -

A — + BV 3V = 0, 8x.

естественные начальные условия (15) в векторной форме запишутся в виде

— 3V = 0.

8 t

Здесь векторы имеют вид (20), матрицы векторного уравнения (21) и граничных условий (22) формируются из коэффициентов системы дифференциальных уравнений (19) и граничных условий (14).

Векторное уравнение (21) с учетом граничных условий (22) и начальных условий (23) решается методом конечных разностей второго порядка точности.

M ^-2 + V^ A V - 2 + ,-_и )+ B V j V -J+ C ( j V J= 0.

Векторное уравнение решаем относительно искомой функции V _{i j} + ₁

• V, . =- M ’ ( hA — B V   2 E + 2 AM T - CM 2 k-

• - M - , =( AL + B ).„ , , - V i^^ CM - T 2 V 0 i,j                      ^,24)

• 2. Анализ результатов численных исследований

f h    2 h 7

Разработаны алгоритм и программа расчета подземных трубопроводов в случае падения сейсмической волны под углом к оси трубопровода, что соответствует произвольному сейсмическому нагружению. В качестве примера рассмотрим следующие задачи.

Задача. Рассмотрим стальной подземный трубопровод: левый конец защемлен, а правый конец свободно оперт. На основе алгоритма компьютерной реализации решается по- ставленная задача. Механические и геометрические параметры выбираются в следующем виде: E = 2-105 МПа; p = 7,8^103 кг/м3; F =

(DH - DB) м2. I = n(dH - dB ) . D = 0294 м

4             ; z 64            ; B ,        ;

D h = 0,30 м; l = 50 м; k x = 3^10 4 кН/м³; д_гру „ _т = 0,2; О труба = 0,3; u o ( x, t ) = Ae

I . x - f l t

C p

sin to t f

x c„ p 7

7 77"

A = 0.002 м; e = 0.3 c^-1; to = —; T = 0,3 с; C, = 2000 м/с. _T         , p

Механизм землетрясений является одним из сложнейших процессов, воздействующих на надземные и подземные сооружения, что затрудняет их расчет. Под воздействием землетрясений возникают колебания подземных трубопроводов, что влияет на их напряженнодеформационное состояние. Результаты решения задач приводятся в виде графика.

На рис. 2 представлены зависимости значений продольного перемещения и нормального напряжения вдоль оси трубопровода от времени при разных углах падения сейсмической нагрузки к оси трубопровода. Процесс рассматривается в условиях, когда трубопровод находится в растянутом или сжатом состоянии (см. рис. 2а – г). Видно, что с увеличением угла падения сейсмической нагрузки к оси трубопровода значения продольного перемещения и нормального напряжения уменьшаются. Этот процесс виден даже в колебаниях в заданных точках трубопровода (см. рис. 2д, е).

Изменение угла падения сейсмической нагрузки к оси трубопровода приводит к поперечному смещению трубопровода, появлению касательных напряжений и изгибающего момента (рис. 3). С увеличением угла падения сейсмической нагрузки от-носительно оси трубопровода до 90° увеличиваются значения поперечного смещения, ка сательного напряжения и изги-

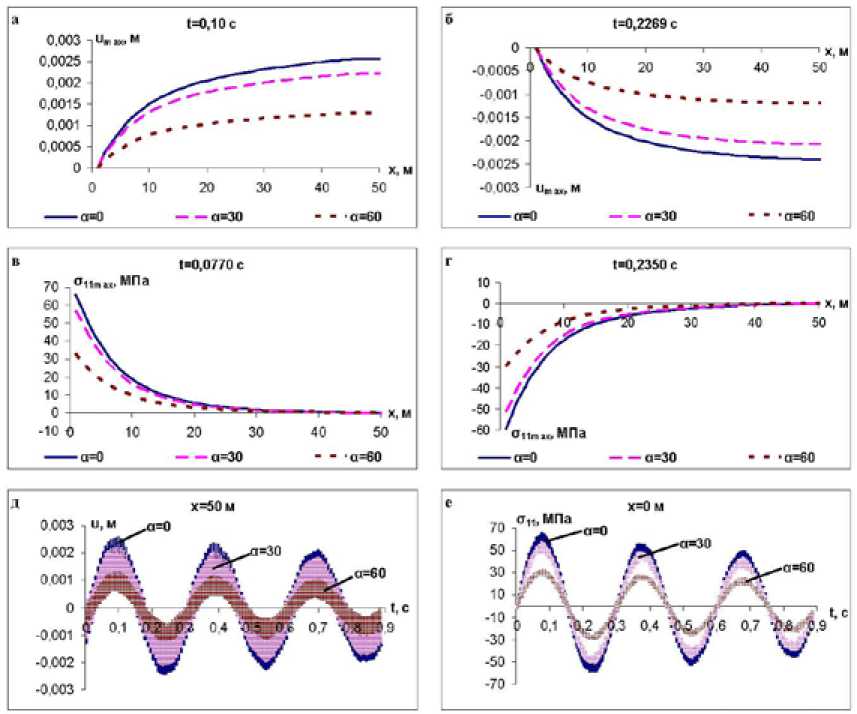
Рис. 2. Зависимости продольного перемещения и нормального напряжения подземного трубопровода от времени и угла падения сейсмической нагрузки к оси трубопровода

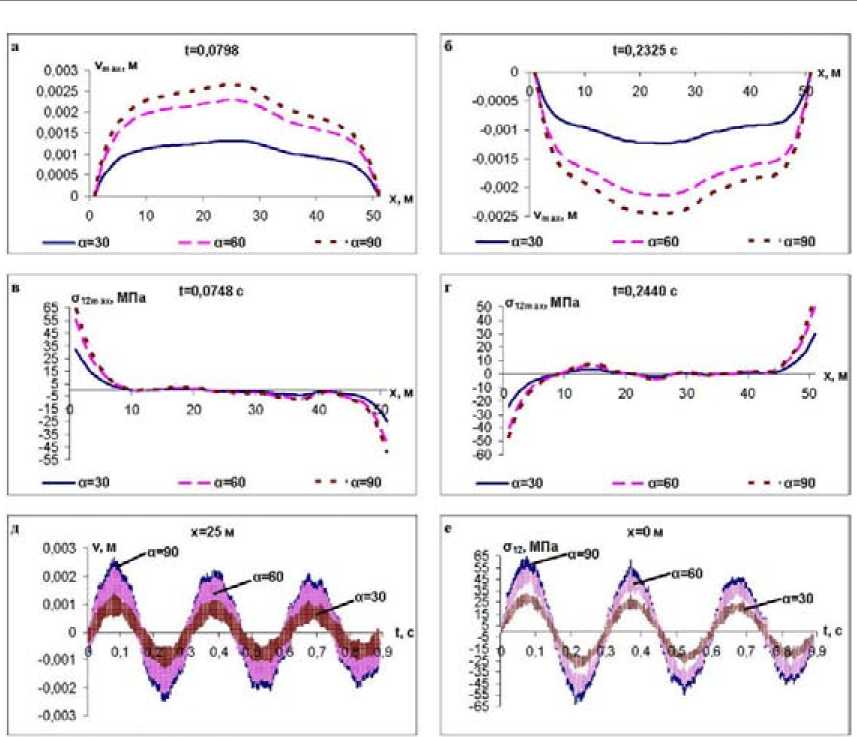
Рис. 3. Зависимости поперечного смещения и касательного напряжения подземного трубопровода от времени и угла падения сейсмической нагрузки к оси трубопровода бающего момента. Изменения значений этих параметров в зависимости от времени по длине трубопровода приведены на рис. 3. Там же приведены колебания поперечного смещения и касательного напряжения в заданных точках трубопровода. Увеличение угла падения сейсмической нагрузки относительно оси трубопровода приводит к увеличению амплитуды колебания поперечного смещения и касательного напряжения (см. рис. 3д, е).

Изменение значения угла поворота оси трубопровода по длине трубопровода и изгибающего момента приведены на рис. 4 и 5 при заданных временах, а также показаны увеличения значений угла поворота оси и изгибающего момента трубопровода при увеличении угла падения сейсмической нагрузки относительно оси трубопровода.

На рис. 5 также приведены колебания изгибающего момента трубопровода в заданной точке трубопровода. Здесь видно, что значения амплитуд колебаний изгибающего момента трубопровода с увеличением угла падения сейсмической нагрузки относительно оси трубопровода увеличиваются.

Если анализировать по рис. 2, 3, нормальное и касательное напряжения своих максимальных значений достигают на защемленном конце трубопровода.

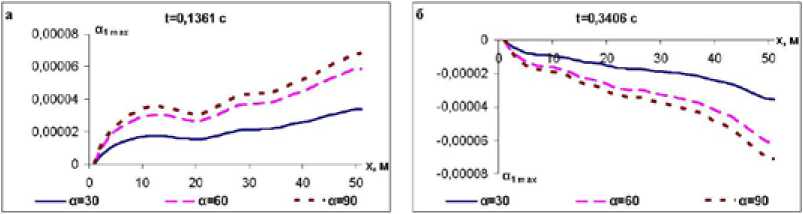
Рис. 4. Изменение угла поворота трубопровода в заданных временах и углах падения сейсмической нагрузки

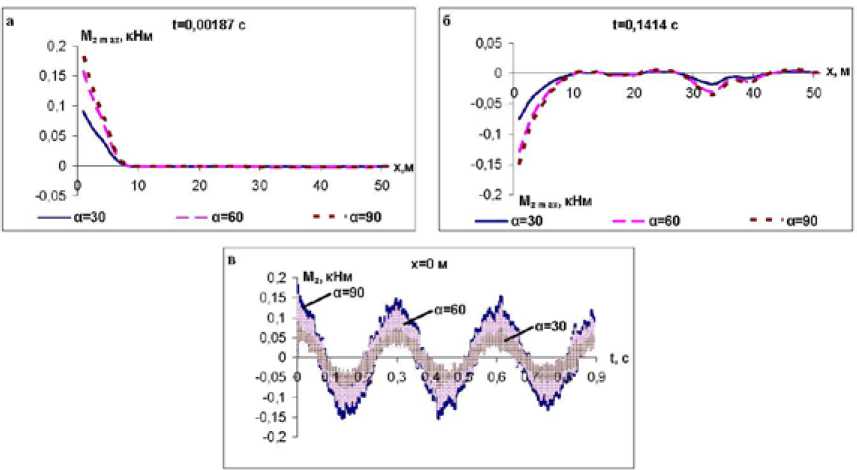
Рис. 5. Изгибающего момента подземного трубопровода

Заключение

На основе вариационного принципа Гамильтона – Остроградского выводится система дифференциальных уравнений колебания подземных трубопроводов с соответствующими граничными и начальными условиями.

Колебания грунта имеют сложный характер. Колебания грунта зависят от структуры грунта. При расчете подземных трубопроводов законы движения грунтов принимаются в виде гармоники, импульса и затухающей гармоники.

Целесообразно было бы при расчете подземных трубопроводов использовать в качестве сейсмической нагрузки сейсмограммы, акселерограммы или велисограммы.

При воздействии сложной сейсмической нагрузки на подземный трубопровод на трубопроводе возникают продольное, поперечное усилия и изгибающий момент. Поэтому для определения прочностных характеристик целесообразно вычислить в опасных зонах (сечениях) трубопровода нормальные и касательные интенсивности напряжений.

Разработанные алгоритмы и программы расчета позволяют рассматривать колебания трубопровода при различных видах нагружения, закрепления концов и параметров грунта. Тем самым все эти процедуры позволяют определить реально возникающие перемещения и нагружения в сечениях трубопровода при различных сейсмических нагружениях. Это даёт возможность для совершенствования нормативных документов сейсмостойкого строительства подземных сетей жизнеобеспечения и создания универсальных программ их расчета и проектирования.