Математические модели, используемые при принятии управленческих решений в условиях риска

Количественные методы используются в бизнесе в течение многих лет с середины 20-го века для расчета срока окупаемости инвестиций и отдачи от инвестиций, оборачиваемости запасов, анализа статистической информации и др. С развитием более мощных электронных вычислительных машин стало возможным моделирование сложных систем. Акцент на использование количественных методов разработки и принятия решений сложных проблем в управлении характерен для научного менеджмента, отличительными особенностями которого являются следующие:

• -    системный взгляд на проблему, принятие во внимание всех имеющихся точек зрения, всех существенных взаимосвязанных переменных, содержащихся в решаемой задаче;

• -    командный подход к решению проблем на основе совместной разработки возможных альтернатив и их обсуждения;

• -    акцент на использовании формальных математических моделей и статистических и количественных методов анализа.

Модель является абстракцией или упрощенным представлением существующей реальности, разработанной, чтобы включать только существенные черты, которые определяют поведение реальной системы.

В научном менеджменте используется пятиступенчатый процесс моделирования, который начинается в реальном мире и развивается в модельном мире, чтобы решить поставленную проблему, а затем возвращается в реальный мир для реализации принятого решения. Концептуальный подход к моделированию в менеджменте предполагает последовательное прохождение по следующим этапам:

• 1.    формулировка задачи (определение целей, переменных и ограничений);

• 2.    построение математической модели (на основе упрощенного реалистичного представления о рассматриваемой системе);

• 3.    проверка способности модели предсказывать явления из прошлого, и ее пересмотр в случае необходимости;

• 4.    анализ последствий различных вариантов принятых решения на базе составленной модели и выбор оптимального решения;

• 5.    реализация выбранного оптимального решения на практике. В случае несоответствия последствий, выявленных в процессе моделирования, реальным последствиям – пересмотр модели.

Научный метод или научный процесс имеет фундаментальное значение для менеджмента. Можно выделить три категории принятия управленческих решений: в условиях определенности, в условиях риска и в условиях неопределенности. В данной статье рассматриваются количественные методы, используемые при разработке и принятии сложных управленческих решений в условиях риска.

В общем виде процесс разработки и принятия управленческих решений можно представить в виде таблицы выигрышей или матрицы решений (табл. 1).

Таблица 1. Матрица решений

Альтернативы	Последствия/Вероятность
	N 1	N 2		N j		N n
	p 1	p 2		p j		p n
A 1	O 11	O 12		O 1j		O 1n
A 2	O 21	O 12		O 2j		O 2n
A i	O i1	O i2		O ij		O in
A m	O m1	O m2		O mj		O mn

Как видно из табл. 1, решение принимается среди некоторого числа ( m ) альтернатив, которые записываются как A 1 A 2 , ..., A m . Будущая ситуация, положение дел или последствия принятия различных решений обозначены как N , их количество составляет n последствий. Эти последствия не могут быть в равной степени вероятны, и каждое из них ( N j ) имеет некоторую (известную или неизвестную) вероятность P j , сумма которых составляет 1.

Исход (получаемая выгода или выигрыш) будет зависеть как от выбранной альтернативы, так и от последствий. Например, если выбрана альтернатива A_i и будет реализовано последствие N j с вероятностью P_i , то выигрыш составит Q ij . Полная матрица решений будет содержать m альтернатив n последствий. Рассмотрим применение представленной модели для принятие управленческих решений в условиях риска.

В процессе принятия решений в условиях риска предполагается, что существует ряд возможных будущих состояний (последствий) Nj в соответствии с матрицей риска (табл. 2). Каждое последствие имеет свою определенную вероятность pj и может быть только одно последствие, которое приводит к лучшему результату для всех альтернатив Ai. Примеры будущих состояний и их вероятностей могут быть записаны следующим образом:

• -    Альтернативная погода ( N 1 = дождь; N 2 = хорошая погода) будет влиять на рентабельность альтернативных графиков строительства. Здесь вероятность p 1 дождя и р₂ хорошей погоды можно оценить на основе исторических данных;

• -    Альтернативные варианты экономической ситуации в стране определяют относительную прибыльность инвестиционной стратегии предприятия. Здесь предполагаемые вероятности различных вариантов экономической ситуации могут основываться на суждениях экспертов-экономистов.

• У читывая последствия принятия решений и их вероятность, принятие решения в условиях риска является альтернативой A i , которая обеспечивает высокий ожидаемый результат E_i , которая раcсчитывается как сумма произведений каждого из результатов O ij на вероятность p j каждого из возможных последствий N j и может быть записана следующим образом:

E i =Lⁿ j=i (P j * O j                              (1)

Например, рассмотрим ситуацию с двумя альтернативными вариантами принятия решений и двумя возможными последствиями (табл. 2).

Таблица 2. Пример принятия решения о страховании имущества в условиях риска

Альтернативы	N 1	N 2
	p 1 =0,999	p 2 =0,001
A 1	–200 тыс. руб.	–200 тыс. руб.
A 2	0	–100 тыс. руб.

Выбор альтернативы A 1 приводит к последствиям, выраженным в прибыли в размере 200 тыс. руб. Выбор альтернативы A 2 - к прибыли в размере 100 тыс. руб., если происходит последствие N 2 , а если оно не происходит - к нулевой прибыли. На первый взгляд, альтернатива A 1 выглядит явным победителем, но представим ситуацию, когда вероятность ( Р 1 ) первого последствия составляет 0,999, а вероятность ( Р 2 ) второго последствия - только 0,001. Ожидаемый результат выбора альтернативы A 2 составляет только:

E(A2)=0,999(0 тыс. руб.)-0,001(100 тыс. руб.)= -100 тыс. руб.

Следует отметить, что, этот результат в -100 тыс. руб. невозможен: если альтернатива А 2 будет выбрана, то потери составят либо 0 руб., либо 1 млн. руб., а не 100 тыс. руб. Тем не менее, если есть много решений этого типа в течение долгого времени, и выбираются варианты, которые максимизируют ожидаемый результат каждый раз, можно добиться наилучшего общего результата. Так как мы предпочитаем ожидаемый результат Е 2 с выигрышем -100 тыс. руб. значению Е 1 с выигрышем -200, мы должны выбрать альтернативу А₂ , при прочих равных условиях.

Рассмотрим данные цифры на конкретном примере. Предположим, что у компании есть имущество (здание), стоимостью 1 млн. руб., и предлагается купить страховку от пожара для него стоимостью 200 тыс. руб. год. Это в два раза превышает «ожидаемую стоимость» потерь от пожара (как это и должно быть, чтобы покрыть стоимость страховой компаний, накладные расходы и расходы страхового агента).

Тем не менее, компания, как и большинство бизнес-структур, вероятно, купит страховку, потому что ее отношение к риску таково, что она не готова принять потерю своего здания. Страховая компания имеет другую точку зрения, так как она страхует много домов и может получить прибыль от максимального ожидаемого результата в долгосрочной перспективе.

Рассмотрим другой пример. Предположим, что у компании есть права на земельный участок, на котором может или не может быть нефть. У нее есть три альтернативы не делать ничего («не бурить»), «бурение за свой счет» стоимостью 500 млн. руб., и «бурение в аутсорсинг» – возможность нанять кого-то, кто будет бурить скважину и в случае успеха поделится прибылью. Предполагается, что существует три возможных последствия бурения: ничего не найдено (убыточно), найдено немного нефти (не выгодно), найдено много нефти (выгодно). Вероятность данных последствий оценена и приведена в табл. 3.

Таблица 3. Пример принятия решения о бурении нефтяной скважины в условиях риска

Альтернативы	Последствия / Вероятность			Ожидаемый результат
	N 1 : убыточно	N 2 : не выгодно	N 3 выгодно
	p 1	p 2	p 3
A 1 : не бурить	0 руб.	0 руб.	0 руб.	0 руб.
A 2 : бурение за свой счет	-500 млн. руб.	300 млн. руб.	9300 млн. руб.	720 млн. руб.
A 3 : бурение в аутсорсинг	0 руб.	125 млн. руб.	1250 млн. руб.	162,5 млн. руб.

Первое, что мы можем сделать, это исключить альтернативный A 1 , поскольку альтернативу А₃ по крайней мере, привлекательными для всех состояний природы и является более привлекательным, по крайней мере одного состояния природы. А₃ поэтому сказал, чтобы доминировать A₁ .

Затем мы можем рассчитать ожидаемые результаты для оставшихся вариантов А 2 и А 3 :

Е 2 = 0,6*(- 500) + 0,3*(300) + 0,1*(9300) = 720 млн. руб.

Е 3 = 0,6*(0) + 0,3*(125) + 0,1*(1250) = 162,5 млн. руб.

После этого выбор очевиден: альтернатива А 2 при условии нашей готовности принять на себя риск в размере 500 млн. руб.

Для принятия решений в условиях риска можно также использовать другую технику – дерево решений. Для начала необходимо составить так называемый узел решений (обычно в виде квадрата или прямоугольника), из которого можно получить количество альтернативных вариантов решений. Каждая альтернатива заканчивается случайным узлом, как правило, изображаемым в виде круга.

Из каждого узла можно излучать несколько возможных вариантов будущего, их вероятность и конечный результат. Ожидаемый результат для каждой альтернативы является суммой произведений результатов и связанных с ними вероятностей. Рис. 1 иллюстрирует использование дерева решений в примере со страхованием здания от пожара. Преимуществом техники дерева решений является ее наглядность.

Варианты решений	Вероят-Последствия Выигрыш                 Ожидаемый результат ность
Страховать	Нет пожара:     -200    *   0,999    =     -119,8

+        = - 200

ожар:        -200     *    0,001    =      -0,2

	Нет пожара:      0      *   0,999   =       0
Не страховать	+        = - 100

Пожар:      -100000   *   0,001    =      -100

Рисунок 1. Пример дерева решений для страхования здания

Другим распространенным смыслом принятия решений в условиях риска является изменчивость результатов, которая определяется с помощью нахождения дисперсии – квадратного корня стандартного отклонения. Рассмотрим два инвестиционных проекта: X и Y , характеризующихся распределением вероятностей ожидаемых денежных потоков в каждом из следующих нескольких лет, как показано в табл. 3.

Таблица 3. Данные риска и дисперсии

Проект X		Проект Y
Вероятность	Денежный поток, тыс. руб.	Вероятность	Денежный поток, тыс. руб.

0,10	3000	0,10	2000
0,20	3500	0,25	3000
0,40	4000	0,30	4000
0,20	4500	0,25	5000
0,10	5000	0,10	6000

Ожидаемые денежные потоки рассчитываются таким же образом, как и ожидаемый результат:

E (X) = 0,10*(3000) + 0,20*(3500) + 0,40*(4000) + 0,20*(4500) + 0,10*(5000)= 4000 тыс. руб.

E (Y) = 0,10*(2000) + 0,25*(3000) + 0,30*(4000) + 0,25*(5000) + 0,10*(6000)= 4000 тыс. руб.

Несмотря на то, что оба проекта имеют одинаковые средние (ожидаемые) денежные потоки, ожидаемые результаты дисперсий (квадратов отклонений от среднего значения) отличаются:

V x =0,10*(3000-4000)²+0,20*(3500-4000)²+…+0,10*(5000-4000)²= =300000 тыс. руб.

V y =0,10*(2000-40000)²+0,25*(3000-4000)²+…+0,10*(6000-4000)²=

=1300000 тыс. руб.

Стандартные отклонения – это квадратные корни этих значений (рис. 2).

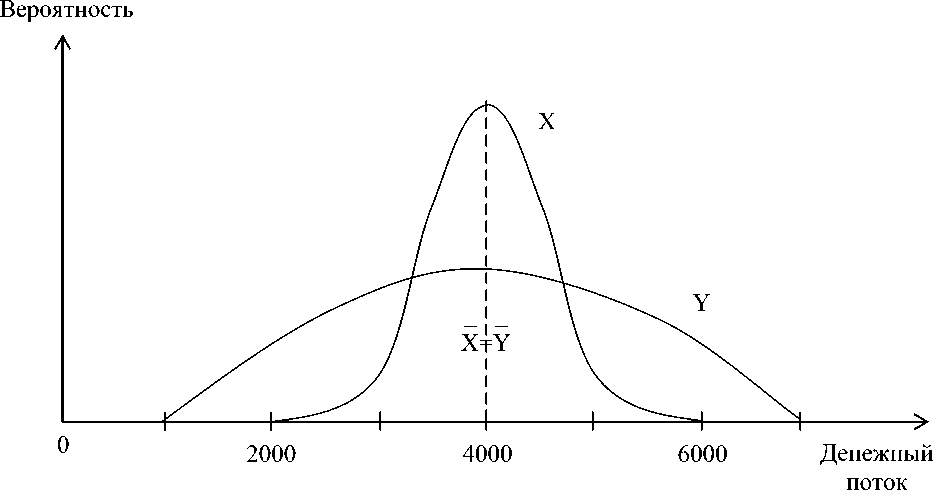
Рисунок 2. Проекты с одинаковыми ожидаемыми результатами, но разной вариацией

Так проект Y имеет большую изменчивость (дисперсию), то он характеризуется большим риском, чем проект Х, который является предпочтительным в данной ситуации, так как предлагает тот же ожидаемый результат с меньшим риском.