МАТЕМАТИЧЕСКИЕ МОДЕЛИ КИРАЛЬНОГО МЕТАМАТЕРИАЛА С УЧЕТОМ И БЕЗ УЧЕТА ИНДУКТИВНОЙ И ЕМКОСТНОЙ СВЯЗИ МЕЖДУ МИКРОЭЛЕМЕНТАМИ

Современный этап развития радиотехники, оптики и физики твердых тел неразрывно связан с созданием и исследованием новых композиционных структур, называемых метаматериалами [1–3]. Их многообразие порождает практически неисчерпаемые возможности использования в сверхвысокочастотном (СВЧ) и оптическом диапазонах. Метаматериалы создаются посредством пространственной композиции некоторых объектов (размер которых зависит от частоты) внутри или на поверхности некоторого контейнера с другими значениями электрофизических, химических и других параметров. В СВЧ диапазоне метаматериал обычно создается путем размещения в объеме контейнера одно- или двухпериодической матрицы из микроэлементов, соизмеримых с длиной волны СВЧ. Такие модели относятся к классу 3D метаматериалов. Также возможны конструкции метаматериалов, когда микроэлементы располагаются на поверхности некоторой подложки. В оптическом диапазоне на первый план выходят так называемые метаповерхности, когда выстраивается композиция из наночастиц. По сути, метаповерхность является двухмерным аналогом классического метаматериала на СВЧ и представляет собой тонкую пленку с расположенными на ней наноразмерными частицами. Такие метаматериалы относятся к классу 2D. Общим свойством метаматериалов является их селективность (избирательность) по частоте, фазе, поляризации и др. При взаимодействии электромагнитного поля с метаматериалом на определенных частотах изменяются фаза, поляризация и другие характеристики падающей волны. В оптике метаповерхности используются для селективного управления светом.

Одним из часто выделяемых классов метаматериалов являются киральные метасреды [2; 4]. Для их создания в СВЧ диапазоне используются зеркально асимметричные проводящие микроэлементы, а в оптическом диапазоне – атомы хиральных элементов или цепочки из наночастиц также зеркально асимметричной формы. Основными свойствами киральных метаматериалов (КММ) являются также частотная и поляризационная селективность, круговой дихроизм, нали-

чие дуплетов волн с круговыми поляризациями и кросс-поляризация поля.

Большинство эффектов, возникающих при взаимодействии электромагнитной волны с КММ, связано с наличием слабой или сильной пространственной дисперсии. Она возникает вследствие того, что искусственная метасреда образована матрицей микроэлементов с фиксированными одинаковыми расстояниями между ними. Часто метаматериал СВЧ диапазона называют искусственным кристаллом.

Основой математической модели кирального метаматриала являются материальные уравнения следующего в ида [ 5–8]: —                  —                               —        —                    —                               —

D = ^o E - i x^ o V o H ; B = m H + i x^ o V o E , (1) где ε – эффективная диэлектрическая проницаемость;

μ – эффективная магнитная проницаемость;

χ – относительный параметр киральности.

Заметим, что наряду с традиционными материальными параметрами (диэлектрической и магнитной проницаемостями) для описания ки-ральности метасреды вводится относительный параметр киральности. Он определяет изменение фазовых скоростей (волновых чисел) для волн с право- и левокруговыми поляризациями, возникающее при появлении в среде киральности. Также здесь можно заметить, что КММ могут быть левыми и правыми, в зависимости от того, какие (левые или правые) формы микроэлементов используются в матрице, его образующей (знак параметра киральности).

Вторым по важности при построении математической модели КММ является учет дисперсии материальных параметров [9–12]. Наиболее часто в научной литературе используется модель Лоренца [4; 10] в качестве дисперсионной модели диэлектрической проницаемости и формула Кондона [12] для дисперсии параметра киральности. Последний факт вытекает из аналогии КММ СВЧ с оптически активной средой из оптики, модель которой построили Луи Пастер и Жан-Батист Био. Здесь уместно заметить, что во многих работах также учитывается дисперсионная модель магнитной проницаемости c полной аналогией с законом Лоренца.

В последние годы математическая модель КММ дополняется моделью интегральной гетерогенности кирального метаматериала. Можно рассмотреть метаматериал как совокупность среды-контейнера и некоторых объемов (цилиндрической, сферической и др. форм), в которых располагаются проводящие зеркально асимме- тричные композиты. Пусть εc – диэлектрическая проницаемость среды-контейнера, будем считать, что она является бездисперсионной. Очевидно, что наличие проводящего микроэлемента в некотором объеме локально изменит там диэлектрическую проницаемость, то есть в этом объеме она станет равной εs. Исходя из того, что каждый узел матрицы представляет такой объем с измененной проницаемостью, то, очевидно, что интегрально метаматериал можно рассмотреть как некоторую среду с проницаемостью εs, некоторым способом распределенную в другой среде с проницаемостью εc. В этом случае можно применять метод компактных групп в теории диэлектрической проницаемости гетерогенных систем для описания гетерогенности КММ в целом [13]. В настоящее время реализованы два способа учета гетерогенности в КММ: на основе формулы Максвелла Гарнетта и формулы Бруггемана [14; 15]. Заметим, что их использование оправдано при небольших концентрациях узлов матриц с микроэлементами, что имеет место в реальных метасредах. Таким образом, с учетом свойства гетерогенности эффективная диэлектрическая концентрация начинает зависеть как от проницаемости контейнера, так и от проницаемости «узла» матрицы и концентрации таких узлов a: e = e(ec; es; a).

Еще одним немаловажным вопросом при построении математической модели КММ является задача расчета резонансной частоты микроэлемента через его геометрические параметры. Одним из наиболее часто используемых способов является применение квазистатического приближения, когда микроэлемент замещается некоторой RLC-цепочкой. В этом случае задача декомпозируется на вычисление емкости, индуктивности и активного сопротивления микроэлемента через его электрофизические и геометрические параметры. Такой подход реализован в работах [14; 15]. Заметим, что при вычислении индуктивности и емкости можно рассмотреть две модели их расчета. В первой модели все микроэлементы считаются обособленными, то есть между элементами-соседями отсутствует индуктивная и емкостная связь. Во второй модели эти связи учитываются. Наличие связей обусловлено действием закона электромагнитной индукции Фарадея, а также существованием вокруг микроэлемента тока смещения с частотой, определяемой падающей электромагнитной волной.

В данной работе будет рассмотрено построение обобщенной математической модели для ки-рального метаматериала с учетом его кирально-сти, дисперсии диэлектрической проницаемости и параметра киральности, а также интегральной гетерогенности метасреды. Затем рассмотрим частную модель КММ с матрицей, в узлах которой расположены микроэлементы конкретной формы и на этом примере рассмотрим, как учитывать индуктивную и емкостную связь между соседними элементами при расчете резонансной частоты. В завершении проанализируем отражение плоской электромагнитной волны с линейной поляризацией от планарного слоя КММ, описываемого построенной математической моделью с целью определения основных электромагнитных свойств описываемой киральной метасреды.

Построение обобщенной математической модели кирального метаматериала

Рассмотрим абстрактный киральный метаматериал. Под словом «абстрактный» подразумевается, что пока не будет учитываться оригинальная пространственная конфигурация проводящего микроэлемента. Будем просто считать, что КММ образован контейнером, в котором равномерно размещены узлы сферической формы, в которые вписаны проводящие элементы, обладающие зеркально асимметричной формой. При этом внутри каждой сферы ориентация кирального включения является произвольной, чтобы в целом КММ был биизотропным и описывался материальными уравнениями (1). В дальнейшем явный вид конфигурации зеркально асимметричного элемента будет конкретизирован при вычислении его резонансной частоты.

Гетерогенная модель

Интегральную гетерогенность КММ учтем по модели Максвелла Гарнетта, и для эффективной диэлектрической проницаемости КММ получим следующее соотношение:

1 + 2аех         s -ес x     sc

^{; s} x                   ,

• 1    - as x           s s + 2s c

  
  

где s c - относительная диэлектрическая проницаемость контейнера;

• s _s - относительная диэлектрическая проницаемость сферической области, в которую вписан проводящий зеркально асимметричный элемент;

α – концентрация микроэлементов в контейнере.

Используя соотношения (2) и (4) для эффективной диэлектрической проницаемости КММ имеем:

е ( ш ) = е с

1 + 2 as _x ( ш )

^{1 -as} x

^S x ( ^ш ) =

£Х -Sc (ш0 -ш2 - i Уш) ^еш0 + 2sc (ш2 - ш2 - iуш)

Соотношения (5) учитывают интегральную гетерогенность КММ и дисперсию диэлектрической проницаемости.

Материальные уравнения

Используя соотношения (1), (3) и (5), получаем материальные уравнения для КММ в формализме Поста, но с учетом интегральной гетеро- генности и дисперсии материальных параметров:

Дисперсионная модель диэлектрической проницаемости

D = е(ш)E - iх(ш)TH;

Как и в большинстве известных научных работ для диэлектрической проницаемости сферической области, занятой микровключением, будем использовать модель Лоренца:

B = цТТ + i х(ш) E;

s(®) = sc

1 + 2as x (ш)1 -asx ’

x

Ss (ш) =

,

ш0 -ш - i уш

sx (ш) =

■^Щ-^Щ-Щ-иЩ-; ^ш2 + 2sc (ш0 -ш2 - iТш)’

где ш ₀ - резонансная частота;

• ^Y - показатель демпфирования;

Q _s - мощность диэлектрического резонанса.

Дисперсионная модель параметра киральности

Для дисперсии параметра киральности будем использовать формулу Кондона:

х ( ш ) =

□хш0ш

,

ш0 -ш - i уш

где Q ^ - мощность кирального резонанса.

х ( ш ) =

^,шш

.

ш0 -ш - i уш

В соотношениях (6) контейнер и сферические области считаются магнитодиэлектрическими, но без дисперсии магнитной проницаемости.

Связь концентрации микроэлементов и расстояния между ними

Пусть сферические области с элементами расположены на расстоянии d друг от друга.

Безразмерная концентрация микроэлементов выражается как:

NV a = —1, V

где N – общее количество микроэлементов;

• V    – объем метаматериала (например, объем параллелепипеда);

• V ₁    – объем сферической области, в которой

22 R ²

^L 1 =^е----- ,

p

где μ _c – относительная магнитная проницаемость

контейнера.

Индуктивность с учетом индуктивной связи

расположен один микроэлемент.

Пусть d 1 = d + 2 R - пространственный период матрицы микроэлементов, где R – радиус сферической области. Несложно показать, что связь между безразмерной концентрацией и пространственным периодом матрицы определяется формулой:

текущего элемента с четырьмя окружающими его микроэлементами:

4 R ²

a =--------7.

( 2 R + d ) ²

L = L 1 ⁺ у,             (11)

где M = Ку1Щ = KL 1 - взаимная индуктивность; K е [ 0;1 ] - коэффициент связи двух проводящих микроэемнтов.

При M = 0 из соотношения (11) получается

Методика расчета резонансной частоты микроэлемента

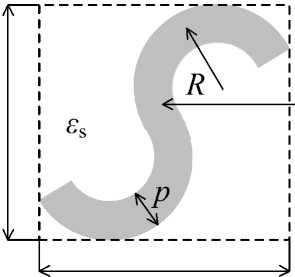
В качестве примера рассмотрим полосковый проводящий микроэлемент S -образной формы, показанный на рисунке 1. Для иллюстрации общности подхода, описанного выше, будем считать, что S -элементы вписаны в кубические объемы с ребром h . Будем считать также, что S -элемент образован полосковым проводником шириной p . Относительная диэлектрическая проницаемость кубической области - s s ( щ ) . Кубики образуют равномерную матрицу внутри диэлектрического контейнера с проницаемостью s c . Радиус закругления S -микроэлемента обозначим через R .

Воспользуемся квазистатическим подходом и будет рассчитывать резонансную частоту микроэлемента по следующей формуле:

^щ 0 = т=,             ⁽⁹⁾

LC

выражения для индуктивности в рамках модели без учета индуктивной связи между элементами.

Из соотношений (10) и (11) имеем:

L = Ц_аЦ

, K А 2^2R²

1 + I-----------

4 ) Р

Интегральная емкость микроэлемента складывается из емкости обособленного микроэлемента и межэлементной емкости, возникающей благодаря существованию тока смещения в пространстве между соседними элементами:

C = C э + С мэ .              (13)

Формула для емкости одиночного микроэлемента имеет вид:

с . = s « s _c2 n Rp .             (14)

h

Межэлементная емкость обратно пропорциональна расстояниями между элементами-соседями:

п Rp

C =s_os ìý 0 c 2 d

.

где L – индуктивность;

C – емкость.

Индуктивность обособленного микроэлемента определяется как:

Из выражений (13), (14) и (15) получаем выражение для емкости системы микроэлементов:

C = 2ns₀s_c Rp

M+h у

4 dh j

d

h

Рисунок 1. Композиция из двух S-микроэлементов

При d ^ да из соотношения (16) получаем фор-

мулу для емкости микроэлемента в рамках модели без учета емкостной связи между элементами.

Из выражений (9), (12) и (16) для резонансной

D) = g(ro; a) E - i /(ro; a) H;B = ^H + i /(ro; a) EL;

частоты получаем следующее соотношение:

c 1

\ C ^Ch   [ L self + L int ] [ ^C self ^{+ C} int ]

,     .      1 + 2agx (ro; a)

g ( ro ; a ) = g _c -------------;

1 -agx

gx (ro; a) =

22 R ²

L self ^—           ; L int ^—

p

2 R ² K ;

2 p ;

_ 2л Rp    _ л Rp

" ~1T ’ ^mt " ~dd ’

Используя соотношения (8) и (16), получаем выражения для резонансной частоты S -микроэлемента через их концентрацию с учетом индуктивной и емкостной связи:

®0 (°) =

c

TeC^Go) ’

G ( «Н L self + L int ] [ C self + C int ( « ) ] ;

2 2 R ²        2 R ² K

Lself =------; Lint = —;—;

p2

_ 2 л Rp л

Cself _       ; Cint (O) _ гT h                            1.

- 1

Используя соотношения (6) и (18), можно записать частную математическую модель КММ на основе равномерной матрицы из кубических ячеек, в которые вписаны произвольно ориентированные полосковые проводящие S -образные микроэлементы (19).

В выражениях (18) и (19): c – скорость плоской электромагнитной волны в вакуум.

Qro0 (a)-gc (ro0 -ro2 -iYro)Q.oy (a) + 2gc (ro0 - ro2 -iyro)

/(ro; «) = ^-; ro0 (a)-ro -1yro

roo (a) =

c

7 gcRc G (a)

; (19)

Отражение волны от планарного слоя кирального метаматериала на основе матрицы из кубических ячеек с S-образными проводящими микроэлементами

Пусть КММ на рисунке 2 образует планарный слой толщины h , неограниченно протяженный вдоль одного из направлений. КММ описывается математической моделью (19), то есть состоит из матрицы кубиков, в которых произвольно ориентированы S -образные микроэлементы. Области 1 и 2 являются вакуумными. На слой из области 1 падает плоская электромагнитная волна перпендикулярной или параллельной поляризации под углом 0 .

Диэлектрическая проницаемость и параметр киральности области 2 являются частотно зависимыми. Структура считается интегрально гетерогенной. Для общности учтена кросс-поляризации поля: при падении волны E -поляризации появляются компоненты H -поляризации и обратно. Внутри кирального слоя 2 возбуждается

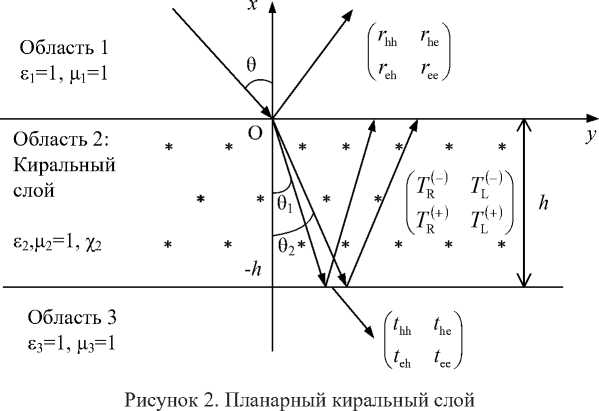
дуплет волн круговой поляризации с противоположными направлениями вращения. В областях 1 и 3 отраженное и прошедшее поле в общем слу- чае эллиптически поляризованное.

Удобно для записи коэффициентов отражения и прохождения использовать матрицы 2x2, учитывающие основное и кросс-поляризованное поле. Так, для коэффициентов отражения имеем:

R =

hh    r he

,

\'eh 'ee J где rhh – коэффициент отражения H-волны при падении H-волны;

r _he – коэффициент отражения H -волны при падении E -волны;

r _ee – коэффициент отражения E -волны при падении E -волны;

^r eh – коэффициент отражения E -волны при падении H -волны.

Для коэффициентов прохождения имеем следующую матрицу 2x2:

T =

t _hh t

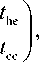
где t _hh

– коэффициент прохождения H-волны при падении H-волны;

t _he – коэффициент прохождения H -волны при падении E -волны;

^t ee – коэффициент прохождения E -волны при падении E -волны;

^t eh – коэффициент прохождения E -волны при падении H -волны.

В слое из КММ возбуждается дуплет из волн с право ( R ) и левокруговыми ( L ) поляризациями, который затем отражается от границы раздела с областью 3. Прошедший дуплет обозначим знаком (–), отраженный дуплет – (–). Матрица размера 2x2 для коэффициентов отражения и прохождения дуплетных волн в области 2 имеет вид:

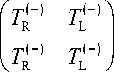
Задача решается методом частичных областей с использованием классических граничных условий для тангенциальных составляющих векторов напряженностей электрического и магнитного полей. Подробное решение задачи приведено в [7; 14].

В результате решение задачи сводится к системам линейных алгебраических уравнений для случая падения электромагнитных волн H- и E-поляризаций:

——          ——

RR = A

B H,E ^R H,E   A H,E^.

R = Гг( ^{- )} Г^{)+ )} T( ^{- )} T⁽⁺ ) r r t f IT- ^R E [ T R , T R , ^T L , ^T L , ' ee , ' eh , t ee , t eh J ;

A _E = [ 1,0,0,cos e ,0,0,0,0 ] T ;

D            ^{( - )} (T⁾⁺ ) (T) ^{- )} (T^{) +} )                         T .

^R H =_ ^T R , ^T R , T L , T L , ' hh , ' he , t hh , t he J ;

A _H = [ o,i,cos e ,o,o,o,o,o ] ^T.

Явный вид матриц B _H,E не приводится в статье, в силу громоздкости их элементов [7].

Анализ численных результатов

При численном моделировании были рассчитаны следующие зависимости физических параметров:

– зависимость резонансной частоты микроэлемента от концентрации зеркально асимметричных композитов;

– частотная зависимость эффективной диэлектрической проницаемости КММ на основе матрицы кубиков, в которые были вписаны S-образные элементы;

– частотная зависимость относительно параметра киральности КММ на основе матрицы кубиков, в которые были вписаны S -образные элементы;

– частотные зависимости прошедшей и отраженной мощностей при падении E -поляризованной волны на слой на основе исследуемого КММ.

Последний тип характеристик рассчитывался посредством численного решения системы линейных уравнений (23) методом Гаусса.

Значения основных параметров задачи приведены в таблице 1.

Таблица 1. Значения параметров

Параметр	Значение
h , м	0,1
R , м	0,055
p , м	0,005
d , м	[ d — h A 1 . _va _
S c	1,5
Ц	1,0
	0,002
Qz	0,001

На рисунке 3 представлен график зависимости резонансной частоты микроэлементов от их концентрации. Как видно из рисунка 3, с ростом концентрации микроэлементов резонансная частота уменьшается. Это связано с увеличением емкостной и индуктивной связи между сосед- ними элементами, в силу увеличения плотности тока смещения, а также наведенного индукционного тока на проводящих полосках.

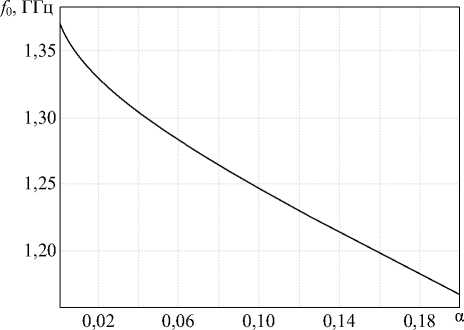
Рисунок 3. Зависимость резонансной частоты микроэлементов от их концентрации

На рисунке 4 приведены графики зависимости эффективной диэлектрической проницаемости от частоты при различных значениях безразмерной концентрации.

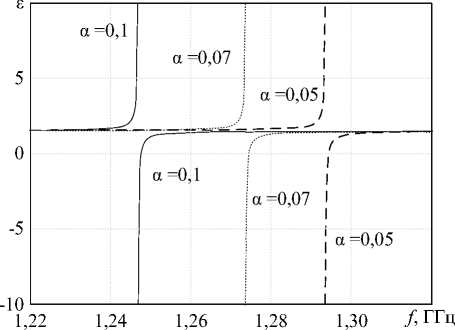
Рисунок 4. Зависимость эффективной диэлектрической проницаемости от частоты

На рисунке 5 приведены графики зависимости относительного параметра киральности от частоты при различных значениях безразмерной концентрации.

На рисунке 6 приведены графики зависимости прошедшей и отраженной мощности основной компоненты поля при а = 0,01. Как видно из рисунка 6, планарный киральный слой на основе периодических кубиков со вписанными в них S -образными элементами ведет себя как диэлектрический слой без потерь. Вся энергия падающей волны проходит через слой, то есть при такой концентрации микроэлементов он является полностью пропускающим (прозрачным).

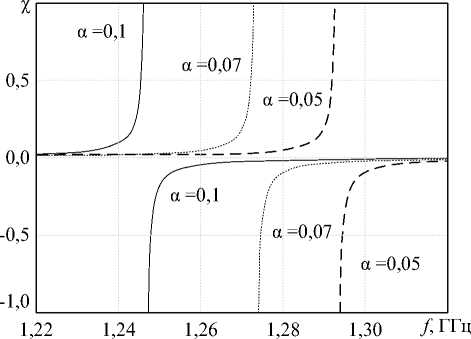
Рисунок 5. Зависимость относительного параметра киральности от частоты

20lg| t ee |

-5

• - 10

20lg| r ee |

• - 15

• - 20

• - 25

• - 30

1,15                1,20                1,25                1,30              f , ГГц

Рисунок 6. Зависимости прошедшей и отраженной мощности основной компоненты поля при а = 0,01

На рисунке 7 приведены графики зависимости прошедшей и отраженной мощности основной компоненты поля при а = 0,03. Как видно из рисунка 7, при увеличении концентрации микровключений возникает частотная селективность кирального метаматериала. Можно заметить, что вблизи резонансной частоты около 1,3 ГГц структура не пропускает электромагнитную волну, при этом практически ее и не отражая. Здесь возникает эффект, связанный с тем, что вблизи резонансной частоты слой КММ поворачивает вектор Умова-Пойнтинга падающей волны на угол 90 градусов, заставляя тем самым ее распространяться в области слоя, подобно оптическому волноводу. На частотах ниже и выше резонансной, слой КММ снова становится пропускающим для СВЧ излучения. Подобный эффект можно использовать при создании маскирующих частотно селективных покрытий с целью запрета связи с объектом на конкретной частоте.

На рисунке 8 приведены графики зависимости прошедшей и отраженной мощности основной компоненты поля при а = 0,05. Как видно из рисунка 8 при дальнейшем увеличении концентрации S -образных микроэлементов так же воз-

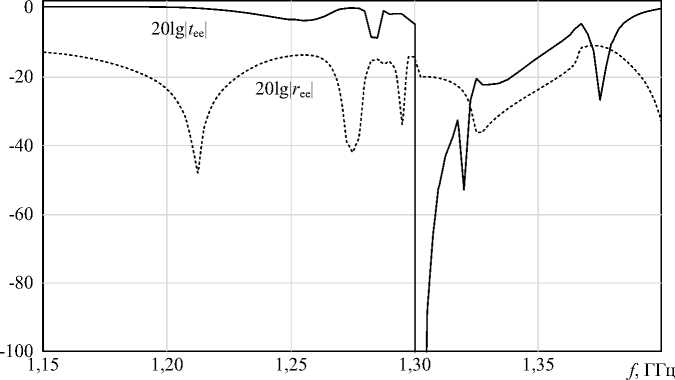
Рисунок 7. Зависимости прошедшей и отраженной мощности основной компоненты поля при а = 0,03

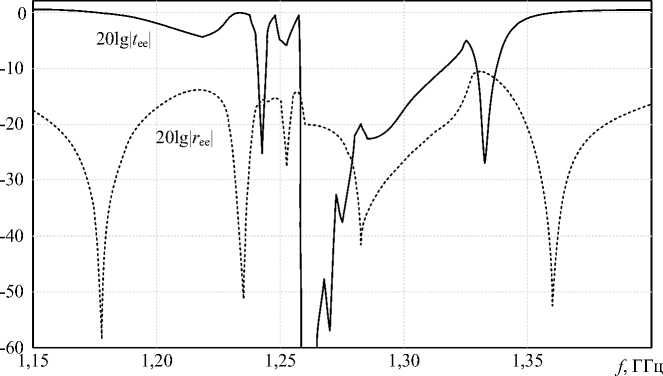
Рисунок 8. Зависимости прошедшей и отраженной мощности основной компоненты поля при а = 0,05

никает частотная селективность КММ, но в этом случае, кроме основной резонансной частоты вблизи 1,27 ГГц, возникает побочная рабочая резонансная частота вблизи 1,33 ГГц. Вблизи обеих указанных частот структура становится не пропускающей для волны E -поляризации.

Аналогичные выводы были сделаны и для случая падения H -волны.

Заключение

Таким образом, в работе описана процедура построения математической модели кирально-го метаматериала, которая учитывает гетерогенность, дисперсию материальных параметров, а также емкостную и индуктивную связь между микроэлементами. Результаты численного моделирования отражения электромагнитной волны СВЧ от планарного слоя показали, что исследуемый КММ обладает частотной селективностью отражения и прохождения. Такой метаматериал позволяет изменять направления вектора Умова-Пойтинга, а именно, вблизи резонансных частот поворачивать его на угол, близкий к 90 градусам, что приводит к возможности переизлучения поля в плоскости планарного кирального метаслоя.

В заключение остановимся на возможных вариантах применения киральных метаматериалов [16– 18]. В настоящее время КММ активно используются при разработке различных СВЧ устройств для изменения фазовых и поляризационных характеристик волн, а также в качестве элементов антенн различного назначения. Другим направлением использования планарных КММ является разработка малоотражающих и маскирующих частотно селективных покрытий объектов, которые на определенных (заранее заданных) частотах спектра СВЧ позволяют подавить отражение от поверхности, на которой расположен киральный метаслой. По сути, в настоящее время наступило время перехода от метаматериалов к метаустройствам [18], принцип работы которых основывается на совершенно новых электромагнитных эффектах.