Математические модели конкуренции: интерференция и эксплуатация

Конкуренция в экосистемах подразумевает такое взаимодействие между живыми организмами, при котором одни организмы используют ресурс, необходимый другим организмам. Такое взаимодействие возможно, как между различными видами, так и внутри одного вида. Особи одного вида имеют сходные потребности в ресурсах, обеспечивающих их выживание, рост и размножение. При внутривидовой конкуренции распределение трофического ресурса, в качестве которого могут выступать свет, жизненное пространство, женские особи, пища и многое другое [1, 2], между особями становится неравномерным. Недостаток ресурса для отдельных групп особей в популяции снижает выживаемость и уменьшает плодовитость.

Участниками межвидовой конкуренции являются несколько видов, использующих один и тот же ресурс, необходимый для выживания особей. Конкуренция возникает только в том случае, если ресурс ограничен [1]. Межвидовая конкуренция разделяется на два основных типа – интерференцию и эксплуатацию. При интерференции особи взаимодействуют друг с другом непосредственно. В случае эксплуатации происходит косвенное взаимодействие через количество потребляемого ресурса. Чем с большей скоростью потребляется ресурс одними видами, тем меньше его достается другим видам. В результате уменьшения потребления ресурса уменьшается и скорость роста численности вида [1]. Как при эксплуатации, так и при интерференции межвидовая конкуренция приводит к снижению плодовитости и жизнеспособности.

Обобщенная модель интерференции Вольтерра. Сегодняшние принципы построения математических моделей популяционной динамики основаны Вольтер-ра [3]. В современных моделях учитывается большее, чем в первых моделях [3], число факторов, определяющих динамику популяций. В моделях Вольтерра не учитывались такие факторы, как ограниченность ресурса, внутривидовая конкуренция, зависимость конкуренции от изменяющихся во времени факторов. Как следует из полевых наблюдений, в условиях конкуренции выживают далеко не единичные популяции [1], в то время как первые варианты моделей видов, оспаривающих одну и ту же пищу, предсказывают выживание только одной популяции [3]. В связи с этим разрабатывается и теория нейтрализма, которая предполагает, что конкуренция, приводящая к гибели популяций, если и была, то была в далеком прошлом [4].

Количественные оценки численности реальных популяций имеют низкую точность. Внешнее вмешательство человека в окружающую среду приводит к фрагментации территории, ее загрязнению, вытеснению видов из их экологических ниш [1, 5]. То есть в модели необходимо вводить антропогенный фактор, как конкурента, не только ограничивающего ресурсы жизнедеятельности популяций, но и изменяющего их структуру [2, 6, 7].

Обобщенная модель Вольтерра для двух популяций предложена А.Д. Базыки-ным в [8] в следующем варианте

dy- = u1(l-ux -/1и2), dt du dt

= / и ₂ (1 - u ₂ - / U ),

где u и u - доли особей популяций от максимально возможного их количества в общей среде обитания, / , / 2 , / - параметры. Внутривидовая конкуренция в (1) характеризуется слагаемыми и² и и 2 в первом и втором уравнениях, а слагаемыми / uUt и // 2 ии - межвидовая конкуренция. Модель (1) при / = 0 и /₂ = 0 переходит в модель двух не взаимодействующих популяций с лимитированным ростом [9, 10].

Особое решение и, = 0 и и₂ = 0 уравнений (1) является неустойчивым, а особые решения и_х = 1 , и₂ = 0 и и_х = 0 , и₂ = 1 могут быть устойчивыми, в зависимости от значений параметров / ₂ >  1 или / >  1 .

Нетривиальная стационарная точка

и1 = (1- /1) / (1- /1/2 ), и 2 =(1 — /2 ) / (1 — /1/2 )

будет устойчивой [8] при одновременном выполнении неравенств / <  1 и / ₂<  1 . В противном случае одна из популяций считается погибшей [1, 8].

Модель конкуренции в группе популяций. Для n конкурирующих популяций система уравнений (1) принимает вид du

— = M i dt

n

и ^{(1 -} и ) ^- и Е № к = 1, k * i

( i = 1,2,..., n ). ⁽²⁾

где м и /д - параметры. Поскольку нетривиальная устойчивая стационарная точка в системе двух уравнений (1) существует при условии, что / <  1 и / ₂<  1 , то в (2) считается, что 0 <  / <  1 ( i = 1,2,..., n ; к = 1,2,..., n ). Эти условия обеспечат существование стационарного решения с двумя нетривиальными компонентами. Стационарное состояние системы уравнений (2) находится как положительное решение системы линейных уравнений

n

Ui + ^Е /ikUk   1   (i   1,2,...,П).

к = 1, к * i

При   /к = 0    ( i = 1,2,..., n ; к = 1,2,..., n )

устойчивой стационарной точкой системы уравнений (2) будет и, = 1 ( i = 1,2,..., n ). В силу непрерывной зависимости решения системы уравнений (2) от параметров / система этих уравнений при малых значениях параметров / будет иметь решение, на котором все его компоненты будут положительными.

Анализ распределения «выживших» в условиях конкуренции популяций из общего количества n осуществлялось следующим образом. Начальные условия и ( t = 0) ( i = 1,2,..., n ), параметры м и компоненты матрицы [ / ] формировалась из набора случайных чисел равномерно распределенных на интервале [0,1]. Системы уравнений (2) решалась с использованием встроенных функций интегрирования систем обыкновенных дифференциальных уравнений математического пакета Matlab.

На рисунке 1 приведено распределение долей «выживших» популяций из 50 изначальных для 10 000 вариантов случайного выбора компонент матрицы [/] и параметров м в зависимости от их числа при среднем значении 10. То есть из 50 конкурирующих популяций в среднем «выживает» 10.

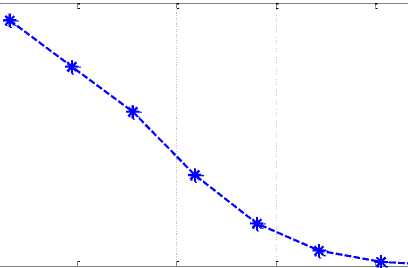
На рисунке 2 приведено распределение «выживших» популяций по численности. Средняя численность выживших популяций 0.25.

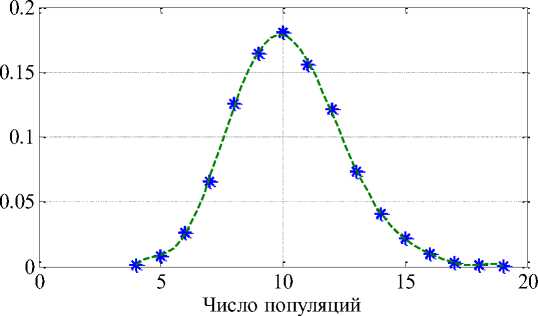
Рис. 1. Зависимость между долей «выживших» популяций и их количеством

=s s У ^

к о к

^ у

0.3

0.2

0.1

0.2

0.4

0.6

0.8

Численность особей в популяции

Рис. 2. Распределение «выживших» популяций по численности особей

Таким образом, из обобщенной модели конкуренции Вольтерра следует, что из всех популяций, вступивших в конкурентные взаимоотношения, небольшая группировка популяций разной численности выживет (рис. 1). Преобладать в этой группировке будут популяции с малой численностью (рис. 2). В обобщенной модели Вольтерра (2) предполагается, что конкуренция происходит в одной экологической нише с участием всех особей всех популяций. В реальных условиях у каждой популяции есть своя экологическая ниша, а конкуренция происходит на перекрывающихся участках с участием только части особей. В дополнение к этому не учитывается и множественность трофического ресурса. Тем не менее, даже при учете толь- ко внутривидовой и межвидовой конкуренций с участием в них всех особей популяций модель предсказывает выживание не одной популяции, а группы популяций разной численности [11]. То есть часть самых приспособленных к конкуренции популяций будет доминировать в ареале, периодически изменяя свою численность [9].

Модель эксплуатационной конкуренции. При эксплуатационной конкуренции особи не взаимодействуют непосредственно между собой, а используют общий ресурс. Модель эксплуатационной конкуренции двух популяций на трофическом ресурсе S , в отличие от модели (1) принимает вид [12].

du

—¹ = ^ u_x dt

S --u.    , b + S ¹

du

-= = ^ 2 u 2

S --u. К + S ²

,

dS = ^S (1 - S / K s ) - a -S-u, dt                      Ь_х + S

—

S au, 2 b2 + S 2’

где ^ и ^ удельные скорости роста численности популяций, а ^ - трофического ресурса, K_s - равновесное количество ресурса в отсутствие популяций. Параметры b и Ь ₂ характеризуют скорость роста численности популяции при потреблении ресурса, а параметры а и а - скорости уменьшения ресурса популяциями. Если ресурс не восполняется, то в третьем уравнении следует положить ^ = 0 . В модели (3) в отсутствие ресурса (при S = 0 ) популяции погибают. С увеличением количества ресурса (с ростом S ) численность популяций увеличивается и при

K

А ^ 1 ’ ^ 2 Ь + K

Два положительных собственных значения обеспечивают неустойчивость этой стационарной точки.

Неустойчивыми будут и стационарные точки, в которых u_x = 0 , u ₂ * 0 и S * K_s или u_x * 0 , u₂ = 0 и S * K_s . То есть стационарные точки, в которых u_x = 0 или

S —— го ( K_s —> ^ ) - u_x —> 1 и u₂ —— 1 . То есть при изобилии ресурса конкуренция прекращается.

В стационарной точке u_x = 0 , u₂ = 0 , S = 0 при ^ * 0 матрица Якоби правой части уравнений (3) имеет два нулевых собственных значения и одно положительное ^ = ^ . Поэтому эта стационарная точка неустойчивая.

В стационарной точке u_x = 0 , u₂ = 0 , S = K_s собственными значениями матрицы Якоби будут

K S

^ 2 , , А ^ 3 '

Ь2 + Ks u2 = 0 на восстанавливаемом трофическом ресурсе будут неустойчивыми. То есть в эксплуатационной конкуренции не погибает ни одна популяция.

Нетривиальная стационарная точка находится из решения системы уравнений ux =

S

Ь_х + S ’

S up              ,

• ²    Ь ₂+ S

  . f ( S ) = - а ,

  
  

  ( S

  
  

  \²

  
  

  I Ь , + S )

  
  

  - ^а 2

  
  

  ( S  ^ ²

  V Ь^ + S )

  
  

  + ^ S (1 - S / K_s ) = 0 .

  
  

Функция f(S) в точке S = 0 обращается в ноль, но является возрастающей, а при S = Ks принимает отрицательное значение. Поэтому на промежутке (0, Ks ) она будет иметь как минимум один корень. Поэтому система уравнений (3) будет иметь хотя бы одну устойчивую стационарную точку.

• u,S

В стационарном положении — =-.

u2S

То есть большая численность будет у того вида, который потребляет больше трофического ресурса в расчете на одну особь ( ux > u2, если b < b). Численность популяций в стационарном положении не зависит от удельных скоростей ц и ц .

Для случая n популяций модель (3) принимает вид du.       ( S

—^L = ц^ --- dt     ‘ i ( S + b

- ^ui

( i = 1,2,..., n ) ,

В нетривиальной стационарной точке

S * u = —---- , ( i = 1,2,

n ),

i S + b ’V а S *

находится как корень уравнения

, * A

M s

1---Нац ii

i = 1

s s

(S *+bi)2

= 0,

которое, как и в случае двух популяций, будет иметь хотя бы одно решение на промежутке ( 0, K_s ) .

Система уравнений (4) решалась с применением численных методов решения задачи Коши для систем обыкновенных дифференциальных уравнений математического пакета Matlab. В качестве параметров a и ц и начальных условий брался набор случайных чисел равномерно распределенных на промежутке ( 0,1 ) , а параметры b - из интервала (1,6). На рис. 3

приведено распределение 50 популяций по численности в стационарном положении для 100 000 вариантов выбора параметров ц , а и b при фиксированном значении параметра K = 60. Цифрами отмечены доли популяций численностью менее 0.35 и численностью более 0.83. Эти границы отмечены вертикальными пунктирными линиями. Популяции численностью более 0.35 и менее 0.83 практически отсутствуют.

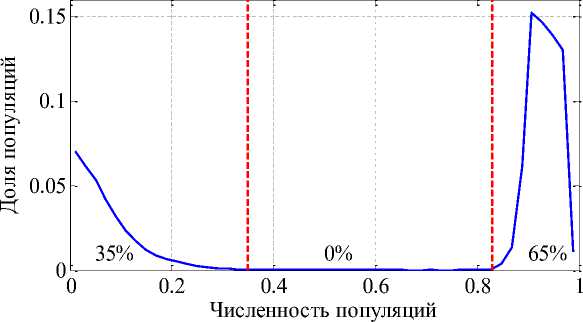
Рис. 3. Распределение популяций по численности

Как следует из анализа полученных результатов, модель (4) предсказывает, что эксплуатационная конкуренция приводит к образованию двух группировок популяций – одна с малой численностью, вторая с большой численностью. При увеличении параметра K (при увеличении трофического ресурса) увеличивается группировка с большей численностью, а с меньшей численностью уменьшается. Уменьшение трофического ресурса (уменьшение параметра K ) приводи к увеличению численности группировки малочисленных популяций.

Заключение. Принцип конкурентного взаимоисключения популяций, сформулированный из анализа первых математических моделей конкуренции, в обобщенной модели Вольтерра относится уже не к отдельным популяциям, а к отдельным их группировкам – выживает не одиночная популяция, а группа популяций. Начальные условия не влияют на наличие равновесного состояния. То есть, на достаточно далеком от начала конкуренции временном расстоянии, при наличии равновесно- го состояния в группе конкурирующих популяций, можно считать, что конкуренция была в «прошлом», а на текущий момент происходит «равновесное конкурентное» потребление одного и того же трофического ресурса в сформировавшейся в эволюционном процессе группировке популяций.

Эксплуатационная конкуренция на возобновляемом трофическом ресурсе не приводит к гибели популяций. Но со временем формируются отдельные группы популяций разной численности. На единственном трофическом ресурсе это могут быть две группировки разного размера – одна с большим количеством особей, вторая с малым количеством особей. То есть при случайном наборе начальных условий и возможностей отдельных популяций произойдет «самоорганизация» всех популяций в две устойчивые группировки, значительно отличающиеся по численности.