Математические модели мыслительных процессов человека (физика сознания)

1. Вступление                          2. Обоснование

R. Penrose и S. Hameroff разработали теорию квантового сознания для объяснения его происхождения [1], к которой научный мир относится довольно сдержанно. Основным в этой теории является то, что они объединили мозговые процессы с фундаментальной теорией пространства-времени (в человеческом мозге происходят квантовомеханические процессы).

Заметим, что многие исследователи считают, что мозг – это квантовое компьютерное устройство, а сознание – его «программа». С дальнейшими их предположениями, что сознание – бессмертная субстанция (существует с момента возникновения Вселенной) и что когда человек умирает, его квантовая информация сливается со вселенским сознанием (изначальной субстанцией), довольно трудно согласиться, поскольку они напоминают идеалистическое (божественное), а не материалистическое (научное) мировозрение.

Далее, по мере обоснования математических моделей, для объяснения наших мыслительных процессов будут упоминаться некоторые предположения S. Hameroff, касающиеся процессов происходящих в мозге.

Напомним некоторые довольно известных положениях, касающихся исследований в области клеточной нейробиологии, высшей нервной деятельности человека.

• 2.1.    Заметим, что убежденность в том, что человек может свободно, сознательно выбирать свои решения, является фундаментальным для нашей картины мироздания. Однако относительно давно известно, в том числе из СМИ, что эта точка зрения не согласуется с экспериментальными данными, полученными в ведущих научных центрах мира, которые указывают, что субъективное восприятие свободы не более чем иллюзия, что решения и поступки определяются мозговыми процессами, скрытыми от сознания и происходящими задолго до появления ощущения принятого решения.

• 2.2.    S. Hameroff предположил в контексте объяснения сознания, то есть состояния, при котором человек осознает себя и способен мыслить, что возможность мозговых квантовых вычислений могут выполнить структуры, известные как микротрубочки, входящие в цитоскелет клеток и состоящие, как известно, из тубулина. При этом в конкретных

местах этого белка электроны вращаются очень близко к друг другу. В этой ситуации возникает и исчезает квантовая когерентность из-за динамической нестабильности микротрубочек, которые то полимеризуются, то деполимеризуются, то есть никогда не пребывают в одном устойчивом состоянии. При этом микротрубочки в одном нейроне могут быть связаны с аналогичными структурами (объектами) в другом.

• S.    Hameroff стремится объединить факт и предположение с целью объяснения, как происходит мыслительный процесс.

Заметим, что в случае 2.1 происходит своего рода «резервирование» информации, которая находится вне организма, или мозга человека. В случае 2.2 нейроны активируются при получении информации. Для более понятного восприятия механизма действия мыслительного процесса представим следующую ситуацию. Например, включим радиоприемник и начнем вращать ручку в поисках конкретной волны. Через некоторое время услышим музыку; вращая ручку дальше – разговорную речь и т. д. Понятно, что мы настраиваемся в резонанс с источником вещания, который может находится относительно далеко.

Проведем аналогию с вышесказанным (назовем это «эффектом радиоприемника» : с одной стороны, за источник вещания условно примем пространство – время с нашим созерцанием и экзистенциальной основой мироздания, с другой – деятельность нашего мозга.

Состояние резонанса (считаем это физической составляющей) между этими сторонами и есть первая (материальная) часть мыслительного процесса, только часть которого находится в мозге (активация нейронов).

Отметим, что всеобъемлющее понятие резонанса уже давно не вызывает вопросов. Очевидно, что в нашем случае резонанс является особым, с квантовой «накачкой». Более коротких мыслей в человеческом организме нет. Мозг только участвует в формировании мыслительных процессов – запоминает, эволюционирует и т. д. Зарезервированная информация (см. 2.1) поступает из пространства–времени с находящимся в нем созерцательно-экзистенциональ-ным содержанием, в результате чего активируются нейроны в нашем мозгу.

В этом случае придется разделить процесс получения информации (см. 2.1), который является материальным (в результате резонанса), и мысли – вторичной составляющей, чего-то абстрактного (образного). Также заметим, что резонанс, связанный с человеком, более сложен, чем «эффект радиоприемника», и у каждого человека имеется свой «резонанс».

Напомним, что в нервной ткани возникают биотоки (биоэлектрические явления) – пользуясь той же аналогией, это вилка, которой радиоприемник перед прослушиванием соединяют с электросетью. Многие делали электроэнцефалографию, и вполне вероятно, что с развитием квантовых технологий (манипуляций со сложными квантовыми системами), с наличием микроскопических датчиков этот «резонанс» удастся зарегистрировать, а кроме этого – отобразить (на аппаратуре) абстрактное «содержание», или вторичное проявление этого резонанса, то есть наши мысли. По ходу изложения будет приведено некоторое подтверждение этому.

Постараемся смоделировать все вышесказанное, существующее в материально-абстрактном аспекте, при помощи математического аппарата из разных разделов математики с целью дальнейших исследований. Напомним, что найти (применить) конкретный вычислительный аппарат, скорее всего будет невозможно. Изложение модельного предложения будет происходить в абстрактном аспекте. Надеемся, что в дальнейшем (с развитием математики) хотя бы в грубой оценке мы приблизимся к каким-то внятным алгоритмам – помня о теореме К. Геделя и ее следствии. Таким образом, исследования должны проходить с «оговоркой» каких-то допущений, критериев.

• 3.    Модельное предложение

Если принять во внимание предположение, что мыслительный процесс находится вне нашего мозга (организма) и проявляется в «форме» резонанса между пространством-временем с созерцательно-экзистенциональном аспектом и активируемыми нейронами в мозге как материальной составляющей (с получением «зарезервированной» информации) и далее отображением всего этого в мыслительный процесс, но с абстрактным «наполнением», то его возможно описать (смоделировать) при помощи математического аппарата, затрагивающего разные разделы математики: алгебраическую топологию в контексте обращения к спектральной последовательности Адамса, при рассмотрении которой имеется связь с числами Бернулли, встречающимися во многих разделах классического анализа и играющие роль «просачиваемости» мыслительных процессов. Эту область приложения (в моделях) необходимо рассмотреть в контексте космологического направления в свете современных теорий и далее – совместно с теорией групп Ли, теорией пересечения (с классами Тодда по У. Фултону), а также комбинаторикой чисел Бернулли. Все эти разделы должна объединить каноническая теория возмущений, где резонансы рассматриваются не как препятствие, а как «подспорье» в контексте развития известной диффузии Арнольда.

Набросок доказательства

За основу в дальнейших рассуждениях возьмем статью [7], в которой в качестве математических моделей приводятся известные положения из вышеуказанных разделов математики, кроме комбинаторики чисел Бернулли и канонической теории возмущения с диффузией Арнольда. Вышеуказанный математический аппарат приведен в этой статье с целью исследования нахождения главной причины старения человека при рассмотрении нашего внутреннего ощущения, что с годами время «летит» быстрее; подчеркнута взаимосвязь с пространством-временем, вплоть до известной М-теории. Заметим, что известное положение, что у старых молекул ДНК короче, чем у молодых, из-за чего кончик нуклеотидной последовательности в процессе жизни оказывается «непрочитанным», то есть каждая копия ДНК в новой клетке становится короче, чем у предшественницы, и поэтому происходит старение организма, является лишь обычным следствием из главной причины, которая рассматривается в [Там же]. Более подробно эта тема освещается в статье, где задействованы такие разделы математики как теория пересечений по У. Фултону [9], спектральная последовательность Адамса [8] и теория устойчивости Ляпунова [10].

Вернемся к моделированию мыслительных процессов. Необходимо учесть, что пространство-время существует вечно, а человек – нет. Поэтому из [7] для рассматриваемого случая подойдет выражение (в связи с тем, что человек существует не в разнотекущем времени по сравнению с М-теорией):

dp\dt = td(E), (1)

где в левой части – фрагмент выражения из теоремы об устойчивости Ляпунова; dp и dt – компоненты импульс и время соответственно (более подробное обоснование см. в [Там же]); в правой – класс Тодда, который связан с числами Бернулли.

z = z (x, y) = x + y + 2 [ x, y ] + 112 [ yx2 ] + ± [ yx2 y ]--L [ xy4 ]-

Г yx4 1 +Г xy3 x 1 +--Г yx3 y 1--Г xy 2 xy 1Г yx 2 yx 1 + 720[   ] 360[    ] 360[    ] 120[     ] 120[     ]

+-- Г xy ⁴ x 1

1440 ^{[    ]}

Г yx4 y 1--Г xy3 x21 + ...

1440[Z Л] 720[     ]

Для случая пространственно-временных отношений из [Там же] существует выражение, определяющее их «просачиваемость» из теории групп Ли, где фундаментальную роль играет формула Кэмпбэла – Хаусдорфа, в которой при любых x,y ∈ Ẑ :

e (x) e (y) = e (z) , где Ẑ – алгебра Ли формальных лиевых степенных рядов.

При этом имеет место известный ряд:

В основе формирования членов приведенного ряда лежат числа Бернулли Bk. Остановимся на алгебраической топологии в части спектральной последовательности Адамса с ее e-инвариантом, в смысле введенного

4r

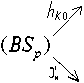
KO4r (BSp)     KO4, (MSp)^^ KO4, (KO)

_; КОДКО)

4,4 ^ (^-^X^CLts0))

Адамсом известного гомоморфизма с вещественным аналогом e _R . Напомним, что если образующую группы π₄(BS_p) обозначить через z*, то образующая из π_8q+4(BS_p) представится в виде y ^{∗ q} z ^∗ , а из π_8q+8(BS_p) – в виде x ^∗ y ^{∗ q} z ^∗ , причем все это рассматривается при отображении f : S ^{4 r} ^ BS p ( q ) сферы в пространство и представлении класса Тома в KO -теории через некоторое отображение. В результате получим коммутативную диаграмму для любого r :

где q – естественная проекция; h_KO‒ некоторая линейная комбинация полиномов Ньютона N _k ; Ф_* μ_lR и J_H ′ ‒ некоторые гомоморфизм^,ы, MS_p ‒ спектр; ( n _L - П _R ) — некоторый элемент, служащий для описания соответствующих диаграмме групп. Остальные компоненты в этой диаграмме – другие разновидности групп. При этом

B

*,* q -1 _*     I2q    4 q_ 4q q eR JH (x y   z ) = 3 „(V u )

I ⁸ q

*

z m (4 q)

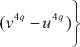
или

B J e r JH ( x* y *^{q - 1} z * )8 q 2^q [ ( v^{4 q} - u ^{4 q} )

для некоторого z ^∗ ∈ Z взаимно простого с m(4g), где v ^{4 q} и u ^{4 q} – элементы, связанные с полиномом Ньютона N_k.

В выражении (4) присутствуют числа Бернулли B _2q Они связывают простран-ственно-врем ^q. енные отношения М-тео-рии. Здесь читатели могут предложить свои модели, похожие или принципиально другие, основанные, допустим, не на рассмотрении чисел Бернулли, а на других математических объектах, а затем по возможности сопоставить.

Заметим, что известная читателям р-адическая система координат в мозге с р-адическими моделями имеют отношение к числам Бернулли, поскольку они связаны с простыми числами довольно известной зависимостью (см. [4]).

Как уже говорилось, в этом случае выражения (3) как модель пространства-времени (вплоть до многомерной М-теории), (4), связанное с (3) и (2), и (1), отражающее жизнедеятельность человека, связаны с числами Бернулли как «критериями просачиваемости» – воздействующего фактора на мозг, где активируются соответствующие структуры (1), то есть сами модели «обеспечивают» своего рода «подготовку» резонанса. Но для его окончательного наступления и мыслительного процесса должна присутствовать, как очередная модель комбинаторика чисел Бернулли. В [2] отмечено, что эти числа управляют топологией бифуракционных диаграмм, что очень важно при рассмотрении самой мысли как абстрактного «содержания», в связи с чем очевидно, что без отображений, то есть без этой топологии не обойтись. Заметим, что комбинаторика в данном случае – это перестановки специального вида – «змей», то есть это и будет «набор» мыслительных процессов.

Рассмотрим главную модель, с которой связано предположение S. Hameroff (2.2) и которая объединит все вышеуказанные модели (с материальным и абстрактным «содержанием»).

Для этого обратимся к другой области математики – канонической теории возмущений, основу которой являются основные положения, восходящие к результатам Н. Н. Нехорошева и В. И. Арнольда. Напомним, что в данной теории [6], центральное место занимает система, определяемая гамильтонианом

H(p,q) = h(p) + e f (p,q),(p,q) e RT,T = R / Z, где (p, q) - переменное действие, угол интегрируемого гамильтониана, е -малый параметр; h(p) - уровень энер- гии; остальные обозначения общеизвестны. При этом выполняется следующая основная оценка:

|| Р ( t ) ^- Р (0)|| ^ R ( е ) ⁽¹³⁾ при

| t *| ^ т(е) и к| ^ ео, где R(е) - радиус удержани; т(е) -время устойчивости; е0>0 - порог применимости.

Заметим, что в этой статье резонансы рассматриваются не как препятствие, а как подспорье (предметом научных изысканий являются резонансные поверхности, замкнутые орбиты, относящиеся к невозмущенной системе). Далее предполагается, что h и / определены и аналитичны в некоторой окрестности начала координат, а именно в комплексной области D = D ( R , q , т ),( p >  0, т >  0) , заданной следующим образом. Пусть B_R -вещественный шар радиуса R с центром в нуле, тогда

D = D ( R, q, т ) =

= { ( p , q е с ² n , dist ( p , B r ) <  p , |lm g | <  ст } .

Обратим внимание на некоторый параметр r, представляющий собой радиус зоны «влияния» вышеупомянутого тора, который в [Там же] присутствует во многих выкладках. Для получения информации об устойчивости точек в фазовом пространстве для любой начальной точки (p(0), q(0)) траектория (p(t*), q(t*)), начинающаяся в (p(0), q(0)), допускает конкретную оценку, восходящую к (Там же). Также в [Там же] описывается эвристическая картина диффузии Арнольда, где за основу берется шар B(p(0), 4s) радиуса 4s и центром p(0)(r0 = 1), где и ищется рациональная точка p с минимальным периодом T, лежащая внутри этого шара. Ученый говорит о «топологической неустойчивости» в контексте вышеупомянутой эвристической картины, то есть «диффузия» – уже последующий тер- мин и в связи с этим также указывается на механизм «расстройки» Нехорошева, т. е. «дрейф» в нерезонансную область.

Кроме этого, скажем о резонансных поверхностях, рассматривающихся как множество точек, содержащих много рациональных векторов.

Заметим, что в вышеупомянутом шаре B(p(0),4м) радиуса 4м (!) с минимальным периодом T точка p(t) может «стохастически» колебаться со скоростью порядка µ внутри шара, но с радиусом 10 µ с центром в p вплоть τ до момента времени t1 = т0exp(—)=).

T 4s

Очевидно, что предположение 2.2 S. Hameroff согласуется с этой теорией как моделью. В ней присутствуют все необходимые элементы: и резонансные поверхности, и время удержания (например, конкретной«мысли»), и зоны влияния тора (задействование конкретной «сферы» контактов нервных клеток относительно простых или сложных мыслительных процессов). Более того, в [Там же] приводятся устойчивое и неустойчивое многообразие тора с «поверхностью» переключения с так называемым «дрейфом» из одной области в другую.

Существенным также является то, что ранее упомянутую комбинаторику чисел Бернулли в контексте рассмотрения «поверхностей переключения» (с одной мысли на другую, то есть с одного резонанса на другой с абстрагированием мыслительного процесса) возможно связать, например, с радиусом удержания в форме какой-то зависимости.

В контексте этих рассуждений очень важно найти эту разумную зависимость. На наш взгляд, является целесообразным дополнительно задействовать раздел математики – потоки на однородных пространствах [3] ‒ в части рассмотрения класса вращения как топологического инварианта.

Значимо то, что эта теория (в контексте развития диффузии Арнольда) подтверждается в разных областях приложения экспериментально, то есть все эвристические рассуждения ученого согласовывается с численными экспериментами. Возможно, приведенные здесь абстрактные модели с их дальнейшим, более предметным, рассмотрением помогут более глубоко изучить проблему мыслительных процессов именно с развитием квантовых технологий.

• 4.    Замечание

В подтверждение данных моделей приведем следующий пример. В научнопопулярной литературе [5] неоднократно описывался сеанс глубокого гипноза, в ходе которого «испытуемый», например, «мысленно переносится» на 300 и более лет назад, ведет диалог в этом состоянии, что самое интересное, от имени другого человека (с другим сознанием), а обстановка того времени описывается им с поразительной точностью. Что это? Мы считаем, что большое и малое повторяют друг друга. Понятно, что наше пространство-время обладает «памятью» (вспомним хотя бы хрономиражи, описываемые в том числе СМИ). В мозге человека, как известно, существует самоподдерживающиеся молекулярные структуры, отвечающие за память. Очевидно, что в состоянии гипноза «память» того пространства-времени (не обязательно хрономиражи) адаптирует под себя мозг пациента, то есть «настраивает» его (или, точнее, его так называемую энергетическую составляющую) в резонанс. Известно, что после смерти человек теряет в весе несколько грамм, – мы считаем, что так «покидает» его эта составляющая (материальная, а не душа). И скорее всего, никакой информации в дальнейшем она не несет.

А ведь так можно договориться до фантастической идеи – не перенести ли сознание конкретного человека в организм другого? Потому как множество людей, в том числе молодых, заканчивает жизнь самоубийством. Или не перенести ли сознание в искусственно созданное тело (как известно, уже действует проект «АВАТАР»-2045)? Проводятся исследования на тему останов- ления или значительного замедления процесса старения организма. В настоящее время все вышеперечисленное относится к области фантастики, но мы надеемся, что в будущем станет возможной хотя бы его часть.

СПÈСÎÊ ÈСПÎËЬЗÎВÀÍÍЫХ ÈСТÎЧÍÈÊÎВ

• 1.    Penrouse, R. Доклад на международном конгрессе «Глобальное будущее 2045» (Нью-Йорк, 16 июня 2013 г.) / R. Penrouse, S. Hameroff.

• 2.    Арнольд, В. И. Исчисление «змей» и комбинаторика чисел Бернулли / В. И. Арнольд // Успехи математических наук. 1992. – Т. 47. – Вып. 1. – С. 3–45.

• 3.    Ауслендер, Л. А. Потоки на однородных пространствах / Л. А. Ауслендер, Л. В. Грин, Ф. М. Хан ; пер. с англ. В. Н. Тутубалина. – Москва : Мир, 1966. – С. 79–82.

• 4.    Боревич, З. И. Теория чисел / З. И. Боревич, И. Р. Шафаревич. – Москва : Наука, 1964. – С. 478–479.

• 5.    Книга тайн ‒ 3 / В. А. Белов [и др.]. – Москва : Мистерия, 1993. – С. 146–147.

• 6.    Лошак, П. Каноническая теория возмущений / П. Лошак // Успехи математических наук. – 1992. – Т. 47. – Вып. 6. – С. 59–140.

• 7.    Проняев, В. В. Объять необъятное : От причины старения до «Большого Взрыва» / В. В. Проняев // Физика сознания, жизни, космология и астрофизика. – 2004. – № 4. – С. 49–55.

• 8.    Свитцер, Р. М. Алгебраическая топология – гомотопии и гомологии / Р. М. Свитцер ; пер. с англ. Ю. П. Соловьева. – Москва : Наука, 1985. – С. 558.

• 9.    Фултон, У. Ф. Теория пересечений / У. Ф. Фултон ; пер. с англ. В. И. Данилова. – Москва : Мир, 1989. – С. 75.

• 10.    Четаев, Н. Г. Теоретическая механика / Н. Г. Четаев. – Москва : Наука, 1987. – С. 243–246.

Поступила 06.02.2015 г.

Об авторе :

Submitted 06.02.2015

About the author :