Математические модели процесса взаимодействия скважинных режущих устройств

В интенсификации любого технологического процесса (в том числе процесса фрезерования) важную роль играет степень совершенства оборудования, предназначенного для его реализации в соответствующих режимных параметрах. Степень совершенства оборудования оценивается спектром эксплуатационных характеристик, по изменениям которого в предыдущих разделах определена граница разделения зон совместимых и несовместимых условий объединения как режимнотехнологических факторов, так и компонентного состава композиционной наплавки. Построены взаимно корреляционные и

автокорреляционные функции между параметрами, характеризующими режущую способность композиционной наплавки и параметрами вектора ее состояния, а также совершенство технологии процесса. Параметры вектора состояния композиционной наплавки классифицированы по степени их значимости, для аттестации которой использован наиболее значимый параметр - относительное удлинение материала матрицы, а для аттестации процесса разрушения - энергия, подводимая к инструменту. Эти зависимости были аппроксимированы следующими уравнениями:

R qq = A- exp(- a t)cos( c t);

^pnq = B •exp(-yt)(cos0t + csinet), где коэффициенты уравнений для рассматриваемого случая имеет следующие значения: А=1; а=0,48; с 0,40; В=0,8; с=0,85; y=0,25; р=19.

Согласно уравнению Винера-Хопфа, определяем весовую функцию, затем применяя интегральное преобразование Лапласа к автокорреляционной функции (1) получаем передаточную функцию процесса в нижеприведенном виде:

Ms) = л

5 + a

(S + a)2 + w2'

(2)

Подставляя значения коэффициентов в уравнение (2) после несложных математических преобразований, окончательно формируем передаточную функцию.

_ 4      S + 0,48

^(s) = Л S2 + 0,96S + 0,3904’

Так как функция выхода связана ч функцией входа выражением x ( S ) = w ( S )· u ( S ) то дифференциальное уравнение процесса разрушения математических объектов фрезерным инструментом, армированным композиционным материалом,

связывающим удельную производительность инструмента с относительным удлинением матричного материала и энергией подаваемой к инструменту на забое, представляется в следующем виде:

^ + 0,96^ + 0,3904% = ^ + 0,48^

dt2       dt              dt где x→q – удельная производительность инструмента; u→(pn) – энергия, подаваемая на инструмент при разрушении скважинных объектов.

Дифференциальное уравнение (4) позволяет решать оптимизационные задачи по проектированию режимнотехнологических параметров разрушения скважинных объектов фрезерными инструментами вооружением из композиционного материала.

Подобными уравнениями приближенно описываются некоторые тепловые объекты, к числу которых также можно отнести процесс фрезерования.

С целью регламентирования режимнотехнологических параметров процесса фрезерования решаем следующую задачу оптимального управления.

Требуется найти алгоритм управления, переводящий объект из положения х = 0; % = 0 при t = 0 в положение х = x n ; % = 0 за минимальное время при ограничении управляющего воздействия

| u | ≤ u max

Непосредственно применить принцип максимума к уравнению (4) нельзя, так как не только высшая производная, но и первая производная может претерпевать разрывы. Для устранения этой трудности применяем метод разложения на множители, запишем уравнение (4) в виде двух уравнений с новыми координатами y 1 и y 2 :

dyi dt

ku;

dy dt2

dy2 0,96^77 dt

-

0,3904 J udt-0,48u.

Новые координаты y 1 и y 2 уже не претерпевают нежелательных разрывов. Выходная координата равна сумме новых координат y 1 и y 2 :

х = y 1 + y 2 .

С переходом к новым координатам изменилась и цель управления: необходимо попасть на прямую (6) и по ней сместиться в начало координат. Указанная задача сво-

дится к задаче с подвижным правом концом. Для решения применяем принцип максимума А.С. Понтрятина. Оптимальное управление в формулировке принципа

максимума, обладает тем свойством, что   функцию Н, называемую Гамильтонианом, оно в каждый момент времени вдоль оп-    причем Н = 0, т.е.

тимальной траектории максимизирует

n max^max/ ^j/j = 0                          (7)

ue0         / '   ' '

7=0

ф | -являются сопряженными функциями и могут быть определены из решения следующей системы уравнений:

n

^2 = - /             (^ = 0'1'2^п)         (8)

at             ' ах\

7=0      1

С учетом функционала

t

J 0 = ^ (100ft — u)²dt ^ min 0

Получаем следующую фиктивную систему уравнений:

^-(/OM-if-J, ; ^--u-J,-, ^-£■4 ; ^r-^-o.^o^-i ;

Согласно (5) составляем сопряженные функции

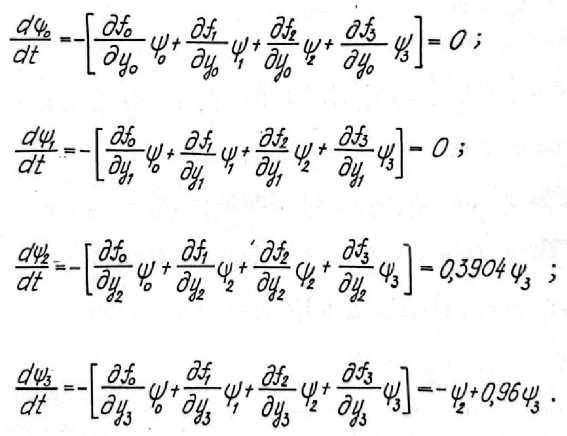
Следовательно,

«^ ; ^ л-мыу; -^-^ч

Для определения ψ 2 и ψ 3 решаем последние два уравнения системы (10):

или же

^.„^dK.d^ Л 0,36 Л df

Решая (12) для определения ψ 3 получаем следующее

ψ 3 = exp(0,48t)(C 3 sin0,4t + C 4 cos0,4t).                    (12)

где C 3 и C 4 – интегральные постоянные. Соответственно, для определения ψ 2 получаем:

ψ 3 = 0,4exp(0,48t)[(1,2C 3 +C 4 )sin0,4t – (C 3 – 1,2C 4 )cos0,4t].         (13)

Согласно (5) составляем Гамильтониан:

0= ро(100п-^ ^ Ч^+Ч^^ ^9О4^ ^ °

-c^oon-o^c^w^exp^s^^^

- ^,2C^cos 0,41] texp(p/8t')(Ci SL/tO^OfCosO’lt)' ^0,36%-0,3004 %-w)-

Определяем уравнение по формуле:

— = 2uC0 + (C1 - 2 • 100nC0) - exp(0,48t) x

x (C3sin0,4t + C4cos0,4t')(0,3904u + 0,43) = 0, откуда

_ [(C1 - 2 • 100nC0) + 0,48exp(0,48t)(C3sin0,4t + C4cos0,4t)]

U=      [0,3904exp(0,48t)(C3sin0,4t + C4cos0,4t) - 2C0]

Интегральные постоянные в (14) определяются согласно граничным условиям, описанным ранее. Так как решаемая задача, является задачей с подвижным правым

концом, то для определения дополнительных интегральных постоянных используются условия трансферсальности, которые записываются в виде

< ψ (0), ξ >=0;

< ψ ( t ), ξ >=0.

Подобная постановка и решение задачи оптимального управления может быть использована для синтеза оптимальных режимно-технологических параметров реализации процесса фрезерования аварийных объектов в условиях скважины фрезерными устройствами.

б) скалярная модель в пространстве состояний.

По результатам экспериментальных исследований выявлено, что автокорреляционные и взаимно-корреляционные функции между входными и выходными параметрами, характеризующими режущую способность композиционной наплавки, ее состояние, а также совершенство технологии разрушения, представляются выражением (1). Согласно уравнению Винера-Хопса

t

Bexp(- Y t)(cos e t + csin e t)

J Аехр(-а1)ео5ш1Ф(1 — z)dT.

Определяем передаточную функцию, для чего применяем интегральное преобразование системы уравнений (2.48):

r . = Rxy(S^ = b[(s + у) + cP][(s — a) + "2]

( ) = Ryy(S)=   A(S + a)[(S + у)2 + P2]

После несложных математических преобразований числителя и знаменателя выражения (16) для определения передаточной функции получаем следующее:

y(S) b0S0 + b1S1 + b2S2 + b3S3 u(S) 1 + a1S1 + a2S2 + a3S3

или же

b0S0 + b1S-1 + b2S-2 + b3S-3

G(S^ =  1 + a1S-1 + a2S-2 + a3S-3 ’ где

,ty^rf№^^   S^a)2)^^)

p ^W^) . в

Учитывая, что функция выхода связана    G(S)^u(S), то перемножив обе части с функцией входа выражением y(S) = уравнения(14)получим

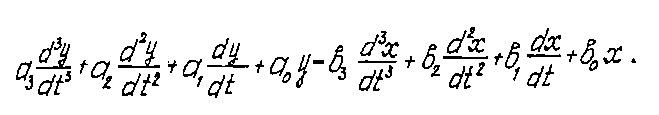
Уравнение (15) можно преобразовать к виду

x(K) = Ф(К - 1) + Ги(К - 1); y(K) = cx(K)

С = [1,0.....0].

Здесь Ф – коагулированная матричная форма /4.33/, а α - нижняя треугольная фунция, обращение которой легко получается подстановкой.

Коэффициент уравнения (15), из которых формируется матрицы Ф и Г для исследуемого процесса принимают следующие значения

b 0 = - 0,331; b 1 = 0,418; b 2 = - 0,41; b 3 = - 0,453; a 1 = 2,235; a 2 = 0,560; a 3 = 0,570.

C учетом значений коэффициентов для указанных матриц получаем

0 Ф =  0

1        0 0     1|;                  (17)

-0,57  -0,56  -2,236

1       0 2,236    1 Г     0,56   2,236 0,57   0,56

0    0 -1 0,4180     0,41801 0    0    -0,410    -1,345 1    0     -0,453      2,320 .           (18) 2,236  1        0        -4,672_|

По видам матриц Ф и Г, согласно выражениям преобразованного уравнения (15) формируем скалярную модель в пространстве состояний исследуемого процесса разрушения металлических забоев вооружением из композиционной наплавки:

У(К) = X1(K);

x1(K) = x2(K - 1) - 0,418u(K - 1);

x2(k) = x3(K - 1) - 1,340u(k - 1);

x3(K) = x1(K - 1) - 0,56x2(k - 1) - 2,236x3(K - 1) + 2,32u(K - 1).

Полученная модель позволяет решать оптимизационные задачи по синтезу композиционных материалов с заданными свойствами.