Математические модели работы перекидного лесопогрузчика с учетом наклона корпуса при наборе груза

При дальнейшем подъеме происходит одновременное перемещение груза вокруг оси вращения стрелы и вращение лесопогрузчика с грузом относительно оси передней балансирной каретки до тех пор, пока задние балансирные каретки лесопогрузчика не встанут на грунт. В момент соударения задней части гусениц с опорной поверхностью лесопогрузчик резко перестает вращаться относительно оси переднего балансира, а груз продолжает вращение относительно оси поворота стрелы.

Это обуславливает возникновение дополнительных нагрузок как на технологическое оборудование, так и на ходовую систему базового трактора. Величина этих нагрузок зависит от массы груза, скорости его перемещения, свойств опорной поверхности погрузочной площадки, а также параметров кинематики и гидросистемы технологического оборудования

Для моделирования работы системы и определения величины возникающих динамических нагрузок в данном режиме необходимо составить расчетную схему и систему уравнений движения технологического оборудования и груза с учетом числа степеней свободы системы «базовый трактор - технологическое оборудование - груз», свойств груза, а также её математическую модель, описывающую движение системы (рис.)

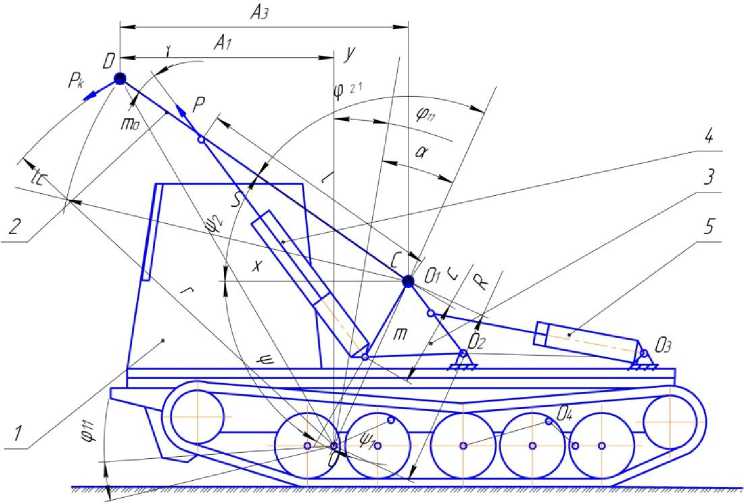
Расчетная схема системы «базовый трактор – технологическое оборудование – груз»: 1 – базовый трактор; 2 – стрела; 3 – поворотное основание; 4 – гидроцилиндр поворота стрелы;

5 – гидроцилиндр поворота основания

Расчетная схема системы представлена на рисунке. Принятые обозначения при составлении расчетной схемы и уравнений движения: т о - масса груза и подвижных частей технологического оборудования, приведенных к точке D; Р к - кориолисова сила инерции; Р - усилие на штоке гидроцилиндра поворота стрелы; l c - длина стрелы; S - длина гидроцилиндра поворота стрелы;, т - масса базовой машины и неподвижных частей технологического оборудования, приведенная к оси вращения стелы (к точке С); О , О 4 -оси вращения, соответственно, переднего и заднего балансиров базовой машины, r, R – радиусы инерции относительно оси О соответственно масс т о и т. Другие обозначения понятны из рисунка. Положение рассматриваемой системы в любой момент времени однозначно определяют параметры - фи, Ф 21 , которые и принимаются за координаты системы. Таким образом, система обладает двумя степенями свободы. Записываем уравнения Лагранжа второго рода:

d  ∂ T    ∂ T

— (---)-- dt дфи   дф ц

= Q

∂ T     ∂ T

— (---)-- dt дф^   др 21

= Q p 21

где Т - кинетическая энергия системы;

Ф 11, P i - перемещения центров масс (обобщенные координаты системы);

Q^  - сила, соответствующая координате р _п;

Q - сила, соответствующая координате р ₂₁;

Кинетическая энергия системы:

Т = T i + Т 2 ,                                                   (2)

где T i - кинетическая энергия масс базового трактора и неподвижных частей технологического оборудования, приведенных в точку О 1 (рис.).

T 1 = 1 . m . r ² . ^² .                                       (3)

Масса груза и подвижных частей рабочего оборудования, приведенная к точке D, совершает сложное движение относительно точки О, вследствие этого её кинетическая энергия представляет собой сумму кинетических энергий переносного и относительного движения.

Т 2 - кинетическая энергия массы груза и подвижных частей рабочего оборудования, приведенной к точке D.

T 2 = ¹⁽ m o • V D ⁺ m o • l C • ^ 221 ^{,                                        (4)}

m o = m 21 + m 30 ,                                                       (5)

где    m 30 – масса жесткого груза, приведенная к концу стрелы;

• V – абсолютная скорость точки D.

Абсолютная скорость точки D равна геометрической сумме переносной и относительной скоростей точки D.

V D = ^RR ' ^ф 11 ^{+ l}C ^{( ф} 11 ^{+ ф} 21 ) ^{+ 2 Rl}C^{( ф} 11 ' ^{( ф} 11 ^{+ ф} 21^{)сО ф} 21 ,                ⁽⁶⁾

где ф₂₁ - угловая скорость массы m о ;

• ф_Х1 - угловая скорость массы m ;

Таким образом, кинетическая энергия системы определяется по выражению:

^T = ¹⁽ m o '1 R^{2 ф} П ^{+ 1}С^{( ф} 11 ^{+ ф} 21^{) 2 + 2} ^ф • ^{( ф} 11 ^{+ ф} 21 ^)с0 Ф 21 ^{) ] +}

²                                                                                            .                 (7)

+ m₀ • 1 2 • ф ) ₂2 + m • R ² • (ф 2 )

Откуда d T дф 11

= 0

-^- = m₀R, j + mJ2,_l + mJ2 ф₂₁ + 2 mJ_cR(_lt cos , ₂₁+ mJ_cR(₂ 1 cos (p ₂i + ^d( P ii

+ mR ²ф_п

d? (—) = moR ' Ф1 + molC Ф1 + mot Ф1 + 2 moWncos, 21 -dt ,n

- 2mJcRфx(ф2j sin(p 21 + mJcR(p2} cos, 21-mJcRф2,ф2} sin(p 21 + mR?ф.

d T д , 21

^- m _o l _c ^RфС sin ( 21 ^- m o ^l C ^R Ф1 ⁽Фи sin ( 21

d T d ^21

= m o^lC Ф11 ⁺ m o^lC ^21 ⁺ m o^lC^R ^11^cos , 21 ⁺ m o^lC ²^21

d- (—) = m o l C Ф 11 + 2 m o l C Ф 21 + m o l C RФп cos

21 - m o l C RФпФ 21 sin

21 dt (₂₁

.

Определение обобщенных сил, соответствующих обобщенным координатам системы . Для определения обобщенных сил Q φ11 и Q φ21 , соответствующих обобщенным координатам φ 11 и φ 21 , применим принцип возможных перемещений. Определим работу сил на перемещениях δφ 11 и δφ 21 координат φ 11 и φ 21 . На систему действуют задаваемые силы: вес подвижных частей технологического оборудования и груза, приведенные к концу стрелы (рис., точка D), вес неподвижных частей технологического оборудования и базовой машины, приведенные к оси вращения стрелы (О 1 ), а также усилия на штоках гидроцилиндров подъема стрелы Р. К заданным силам относится также кориолисова сила инерции. Возникновение кориолисовой силы инерции объясняется тем, что переносное движение в рассматриваемом режиме является вращательным (вращение точки С относительно точки О), а при вращательном относительном движении стрелы с грузом возникает поступательное движение центра масс груза и подвижных частей технологического оборудования, приведенного к оси вращения захвата относительно оси передней балансирной каретки базовой машины. Составим сумму элементарных работ задаваемых сил для относительного движения стрелы с грузом на возможном перемещении δφ 21 . В эту сумму входит работа веса груза и подвижных частей технологического оборудования, приведенного к концу стрелы, вес неподвижных частей технологического оборудования и базовой машины, приведенный к оси вращения стрелы, а также работа кориолисовой силы инерции.

Q,. = m • g • A, - P • l •

(p 21        o О 3

1- (

2 l ²

- 2lc cos(180 - щ

2 lS

- Щ 1 - , 21 ) )2

0,5

Таким образом, кориолисова сила инерции масс элементов конструкции повышает нагруженность системы и при определении обобщенных сил, соответствующих обобщенным координатам, её необходимо учитывать.

Скорость поступательного движения центра масс груза и подвижных частей технологического оборудования (рис.):

0 21 • lc • ^sin( 18 ⁰ - ^ 21 )

7 0 + R ² — 2 l₍R cos(180 — 0 ₂ i)

Кориолисова сила инерции:

P                 .  ⁰ 21 • l c •^{sin(180 —} 0 21 )

^pk = ² m o ⁰11    ----;---------------------

7 Iq + R — 2 l^R cos(180 — 0 , [)

Работа на перемещении δφ 11 :

A 1 = Q 0_n • 60 11 ,

O               A           f                   '         01 Г lc '• Sin(180 — 0 21)

Q0 11 = mo ■ g • A 1 ^— mo ■ g • ⁽ A 3 ^— A 1 ) ^{+ 2} mo ■ 0 11 • I 2     2                          • r . ⁽¹⁵⁾

7 1 2 + R ² — 2 l_cR cos(180 — 0 ₂ J

Найденные выражения производных и правых частей (10), (15) подставим в уравнение Лагранжа и после преобразований, получим систему уравнений:

m o ^{R 0 +} m o ^l C ⁰ 11 ⁺ m o ^l C ⁰ 21 ^{+ 2} m o ^l C ^{R 0} 11 ^cos 0 21 ^—

— 2 m_ol_cR0_xx0₂ j sin 0 ₂₁ + m_ol_cR0₂ j cos 0 ₂₁ — m_ol_cR0₂₁0₂ j sin 0 ₂₁ +

+ m^{R 2}0ц = m o • g • A 1 ^— m o ■ g • ⁽ A з ^— A 1 ) +

+ 2m          _ 0 21 • l c '^sin(180 — 0 21 )      т

^{+ 2} m o ⁰ 11 r^-----~------------------------ r

7 1 2 + R ² — 2 l_cR cos(180 — 0 ₂₁)

m o ^l C 011 ^{+ 2} m o ^l C 021 ⁺ m o l C^R011 ^cos 0 21 ^— m o l C R⁰"? 21 ^sin 0 21 ⁺

^{+ m} o l e ^R (Pi 1 ^sin 0 21 ⁺ m o l e RPn⁰ 21 ^sin 0 21 = m o • g • A 3 ^—

—

P • l •

2 l ²

1 — (---

—

2 lc cos(180 — 0 — 0 — 0 ₂₁)

2 lS

0,5

)

Уравнение (16) описывает движение приведенных масс в системе «базовый трактор – технологическое оборудование – груз», решая которые, можно получить данные о динамических нагрузках, возникающих в элементах конструкции лесопогрузчиков с жесткой и жестко балансирной подвеской корпуса базовой машины в зависимости от конструктивных и эксплуатационных факторов.

Заключение. Из уравнения (16) следует, что работа лесопогрузчика перекидного типа с изменяющимся центром вращения технологического оборудования и груза имеет отличительные особенности:

• 1.    При перемещении технологического оборудования из положения набора в транспортное положение на первом этапе движении происходит вращение груза со стрелой относительно оси вращения стрелы при наклонном положении машины до достижения равенства удерживающего и опрокидывающего моментов от сил тяжести машины и груза.

• 2.    После превышения величины момента от силы тяжести машины (удерживающего момента) величины момента от силы тяжести груза (опрокидывающего момента) происходит одновременное вращение груза относительно оси вращения стрелы и всей машины относительно оси балансира передней каретки до соударения задней каретки с опорной поверхностью.

• 3.    Разработанная математическая модель одновременного перемещения груза вокруг оси вращения стрелы и вращения корпуса лесопогрузчика относительно оси передней балансирной каретки трактора позволяет проводить исследования нагруженности элементов конструкции лесопогрузчика с учетом ряда конструктивных и эксплуатационных факторов (угловой скорости стрелы и корпуса, величины массы груза, параметров кинематической и гидравлической схем и других), выполнять оптимизацию параметров кинематики технологического оборудования на стадии проектирования.