Математические модели раскроя лесосырья в задачах планирования и управления лесопильным производством

ОПИСАНИЕ ПРЕДМЕТНОЙ ОБЛАСТИ

В рамках модели к производственным ограничениям линий лесопиления относятся следующие [2]:

• •    ограничение сверху на количество пил 1-го и 2-го рядов для линии лесопиления;

• •    толщина пропила для каждой линии (мм);

• •    максимальная высота и ширина постава;

• •    минимальная ширина двухкантного бруса, получаемого при первом проходе из бревна путем срезания двух боковых частей, которая устанавливается для каждого диаметра.

К важнейшим ограничениям, обусловленным структурой заказов, можно отнести следующие:

• •    минимальная и максимальная длина пиломатериалов, а также шаг, с которым обрезается пиломатериал (например, при длине 2,7–6 м и шаге 30 см доска длиной 3,5 м должна быть обрезана до 3,3 м, что снижает полезный выход);

• •    специфические требования по размещению пиломатериала относительно бревна: в брусовую часть, то есть выпиливать только из двухкантного бруса [4]; в боковую часть, то есть размещать пиломатериал только для распила при 1-м проходе; 2 x k Ex Log, то есть только в центре бревна и в количестве 2 k шт. (без центральной доски); 2 x k + 1 Ex Log, то есть только в центре бревна и в количестве 2 k + 1 шт. (с центральной доской); 2, 4, 6 Ex Log, то есть только в центре бревна и без центральной доски.

Предположим, что задано множество N всех возможных способов раскроя отрезка ствола дерева на пиломатериалы множества M [3].

Тогда полагаем bi и Bi – ограничения сверху и снизу на объем пиломатериалов i ∈ M, cj – ожидаемый доход от реализации 1 м3 пиломатериалов, распиливаемых по схеме j ∈ N, xj – объем, распиливаемый по данной схеме. Ai j – выход пи- ломатериала i ∈ M при распиле единицы лесо-сырья по схеме j ∈ N. Получим следующую задачу оптимизации:

cx → max, b ≤ Ax ≤ B , x ≥ 0.

Полученная задача весьма условна, ее вариантам будет посвящена следующая статья. В данной работе рассматривается частный вопрос построения столбцов матрицы A [ N, M ], необходимый при использовании симплекс-метода.

ФОРМАЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ ПОИСКА ОПТИМАЛЬНОГО СТОЛБЦА

Введем обозначения, используемые в математической модели.

Исходные данные: N – множество пиломатериалов; t_j – толщина пиломатериала, j ∈ N ; w_j – ширина пиломатериала, j ∈ N ; l^m j – минимальная длина пиломатериала, j ∈ N ; l^M j – максимальная длина пиломатериала, j ∈ N ; ^{s l} j – шаг длины пиломатериала (например, длины 2,7– 6,0 с шагом 0,3 м), j ∈ N ; b_j – признак «брусово-сти» пиломатериала, 1 – «брусовый», 0 – иначе, j ∈ N ; u^b – минимальная доля объема «брусовых» пиломатериалов; ^{u s} j – максимальная доля выхода пиломатериала из боковой части, j ∈ N ; ^{v l} j – двойственная оценка пиломатериала, j ∈ N ; v^w – двойственная оценка древесины; v^m – двойственная оценка линии лесопиления; v^b – двойственная оценка ограничения на минимальную долю брусовых пиломатериалов; ^{v s} j – двойственная оценка ограничений на максимальную долю для постановки пиломатериала в боковую часть, j ∈ N ; d^m – диаметр бревна в узкой части (вершина дерева); d^M – диаметр бревна в широкой части (основание дерева); l^w – длина бревна; V^w – объем одного бревна; c^w – стоимость 1 м³

древесины; ^c j – стоимость 1 м³ пиломатериала, j e N ; s1 - толщина пилы при распиле двухкантно-го бруса; s₂ – толщина пилы при первом проходе.

Неизвестные

Разобьем постав на 2 части – брусовая часть и боковая часть при первом проходе. В случае развального способа распила боковая часть пуста – таким образом, математическая модель охватывает большое количество различных линий лесопиления (рис. 1).

^{l b} p – длина пиломатериала на позиции p в брусовой части, рассчитывается следующим образом:

mint /“, i¹'

, еслиу’р +t

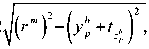
Г.

S

s h, иначе.

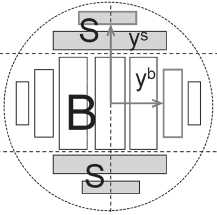
Рис. 1. Разбиение постава на 2 части, расстояние от центра до пиломатериалов

где r^m

d ^m

2,

rM

dM

2,

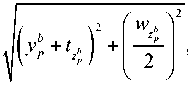
t

— d

P^b – множество позиций для размещения пиломатериалов в брусовой части бруса (для

^{z s} p – номер пиломатериала, помещенного на p -ю позицию постава в боковой части; y^s p – расстояние от центра постава до пиломатериала в боковой части; l_p^s – длина пиломатериала на позиции p в боковой части.

Обозначим W^b – ширина полученного двух-кантного бруса:

пиломатериалов, расположенных симметрично

относительно центра постава, итоговое количество пиломатериалов умножается на 2, для пиломатериала в центре (в случае наличия такого) прибавляется 1). Считаем, что позиции пронумерованы по удалению от центра бревна. P^s – множество позиций для размещения пиломатериалов в боковой части при первом проходе.

z^b_p – номер пиломатериала, помещенного на p -ю позицию постава в брусовой части. ^y p –

W^b = max { w _b } .

p e P z p

W^c – ширина центральной части двухкантно-го бруса:

W^c = 2 max! y^b + 1 b p e P I p z p

1 w₄ = W^b

q_p – кратность пиломатериала на позиции для брус ^p овой части

расстояние от центра постава до пиломатериала (который в сечении представляет собой прямоугольник) в брусовой части. Для центрального t b

b пиломатериала расстояние y^b_p

z ^b

= —. На рис. 2

q p

выделен пиломатериал, для которого расстоя-b          zbp ние Уp = - - .

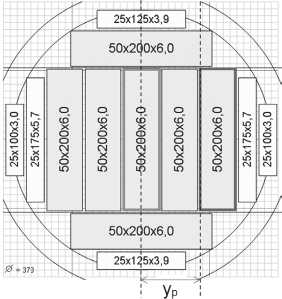
Рис. 2. Четное и нечетное размещение пиломатериала в поставе

b         z p

• 1,    если y_n =-- ,

^p     2

tb b         zp

• 2,    если y_n ^ . p 2

g_p – признак того, что пиломатериал на позиции p e P располагается в боковой части

g p

1, если w b <  W b , z p

0, если w b = W b .

z ^bp

Ограничения

• Позиции пиломатериалов идут в порядке удаления от центра, и расстояние между пиломатериалами равно толщине пропила:

bb yP - Ур-1

ss

Ур - Ур - 1

= t b

= t s ^z

z p - i

s zp-i

^{+ S} 1

+ s 2

• Ширина пиломатериалов не возрастает:

w b, < w p pp        zp-1

для каждогоp e { 2..| p * | } .

w s <  w s для каждого p e { 2.. P s } . z p         z p - 1

• •    Пиломатериалы из двухкантного бруса не пересекаются с пиломатериалами из боковой части:

wb

^p^p yp> — + s2.

• •    Размещение пиломатериала на первой позиции (база):

s                   tzb yb = у илиyb = --^ , Ух = ^ ■ p-

• •    Пиломатериал принадлежит группе D_2xk (требование 2 k Ex Log, k e N ):

  ^V j ^e D 2x k  >

  
  

b s 1

y1   2, bb   b z1 = z2 = ... zk = j,

Z q p = 2 k .

p e ^P . z p =j

• •    Пиломатериал принадлежит группе D_2xk+1

(требование 2 k + 1 Ex Log, k > 0, k e Z ):

y 1 ^b

t b z_p

2,

V j e D 2x k +i ^Ы = z p = ... z^b_k+i = j ,

Z   q p = 2 k + 1.

P e P b , z bp = j

• •    Пиломатериал принадлежит группе D_e (требование четный Ex Log – распил без центральной доски, например 2, 4, 6 Ex Log):

3k e N; z^b = z^b = ... z^b = j и Z 4_P⁼2k.

• •    Пиломатериал принадлежит группе D – не i a , b

менее, чем a Ex Log, но не более, чем b Ex Log:

^J G Di.k

• •    Пиломатериал принадлежит группе D_nm : ∀ p : z^b_p ∈ D_nm ⇒ y_b^p ≠ ^s ₂ ¹ и y_b^p ≠-₂ ^{z bp} .

• •    Количество различных пиломатериалов в поставе не превышает M^d :

| {{ z^bp , p e P^b } U { z p , p e P^s }}| < M d .        ⁽³⁾

• •    В поставе отсутствуют близкие по размерам пиломатериалы, то есть разница по толщине между любыми двумя пиломатериалами

  Максимальная ширина          Максимальная ширина

  пиломатериалов в боковой части          боковой части

  

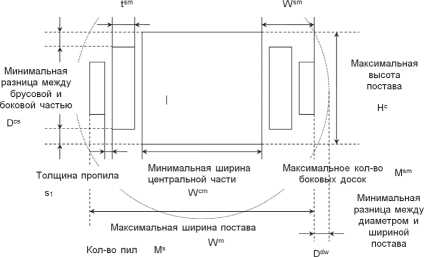
  Рис. 3. Параметры постава на схеме

  
  

либо равна 0, либо не менее чем t^d , аналогично по ширине либо 0, либо не менее W^d :

Минимальная ширина центральной части бруса не менее заданной для линии лесопиления W^{: m} : W c >  W cm .

• •    Максимальная ширина постава не превышает заданную для линии лесопиления W^m :

2 max f v^b + p,! <  W^m. peP* ( " ^P -/J

• •    Максимальная высота постава H c : W^b <  H c .

• •    Разница между диаметром и шириной постава не менее заданного для линии лесопиления D^dw (параметр необходим для того, чтобы в случае использования фрезерного станка для выпиливания боковой части не было слишком тонкой части):

d m - 2max y^b + t _b >  2 D^dw . p e P ^b      p    zp )

• •    Используемое количество пил не превышает заданные параметры для линии лесопиления M ^{s 1} и M ^{s 2} :

Z q p + ¹ <  M^{$ 1},2 /' ■ 2 1/ .

p e P ^b

• •    Максимальное количество боковых досок в двухкантном брусе M^sm :

  { p e P^b : w z p <  W^b }

  
  

  < M^sm .

  
  

• •    Максимальная ширина боковой части боковых досок в двухкантном брусе W^sm :

max! y^p + 1 w ь <  W^b ! - min! y^p I w „ <  W^b | <  W sm .

p e P ^b yp zpl z p          j pe P ^b I p I z p          j

• •    Максимальная толщина боковых досок в двухкантном брусе t^sm :

V p e P^b : w p <  W b ^ t b <  t sm . z_pz_p

• •    Аналогичные параметры по максимальному количеству боковых пиломатериалов, суммарной ширине боковой части и максимальной толщине боковых досок для позиций P^s .

• •    Минимальная разница между брусовой и боковой частями не более заданного для линии лесопиления D^cs :

Wb

—

max

p e P b

I w I

w

W1 }

> 2 D c .

Для поиска оптимального столбца необходимо решить задачу: — vA j + c j ^ max. В данном случае матрица A – генерируемая матрица, каждый столбец которой представляет собой выход продукции каждого вида из постава, а также

Рассмотрим подзадачу поиска оптимального распила одной из частей бревна (возьмем для примера часть 2). Введем параметры: y – текущее расстояние от центра бревна; s – текущее используемое количество пиломатериалов.

Таким образом, для каждого состояния пытаемся добавить каждый пиломатериал и осуществить переход от состояния ( y , s ) к состоянию ( y + t_j + s₁, s + 2 ) (рис. 4).

В результате указанного разбиения задача может быть решена методом динамического программирования, а итоговое решение собирается из 3 частей. Укрупненная блок-схема алгоритма приведена на рис. 5.

вспомогательные элементы для прочих ограничений. Поскольку целевая функция c представляет собой суммарную долю выхода продукции из постава, то при расчетах нельзя брать ее как константу, так как в нее входят неизвестные выходы пиломатериалов [1]. Рассмотрим вариант целевой функции по оптимальному выходу, по доходу – аналогично.

Обозначим P = | P b U P s } (считаем, что множества P^b и P^s не пересекаются по индексам).

В исходной задаче ограничения на брусовые пиломатериалы и на максимальную долю выхода боковых досок выглядят следующим образом:

XX Ai. ( ub — bi) x.^ 0, XX Ajj b’j— ui )* 0, j e N i e L                             j e N i e L где bis, j – доля выхода пиломатериала i из поста-ваj из боковой части.

Тогда целевая функция генератора выглядит следующим образом: ^^^и.^-Ч«^ь-Ь--А-’<_8р-<^-

• - V^й' - v^m max.

АЛГОРИТМ ПОИСКА ОПТИМАЛЬНОГО ПОСТАВА

Для решения данной задачи разобьем множество неизвестных позиций на блоки (рис. 4):

• 1.    Центральная часть основного прохода | p e P^b : w, = W b } ;

• 2.    Боковая часть основного прохода

• 3.    Боковая часть первого прохода { P^s }.

| p e P^b : W b <  W^b } ^;

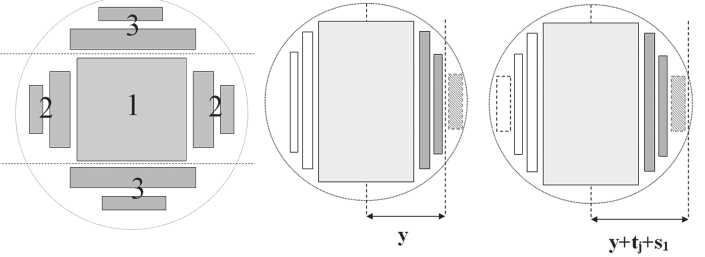
Рис. 4. Разбиение постава на блоки. Переход в динамическом программировании

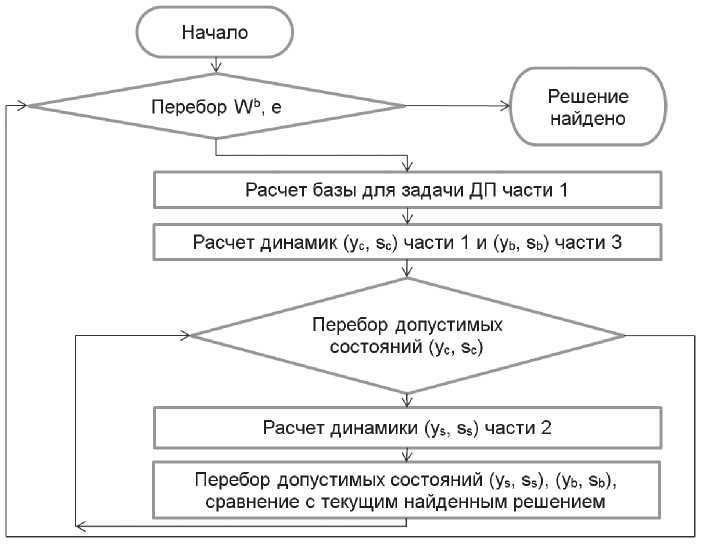
Рис. 5. Алгоритм решения поиска оптимального постава

Теорема 1 . Алгоритм находит оптимальное решение исходной задачи.

Доказательство.

Рассмотрим оптимальное решение ( y^b* , z^b* , y^s* , z^s* ) . Ему по формуле (1) соответствует W^b*. Поскольку в алгоритме перебираются все возможные W^b , искомое значение W^b* будет рассмотрено.

Далее пусть оптимальному решению соответствует W^c* (формула (2)). Поскольку в алгоритме перебираются все возможные значения W^c , то искомое значение также будет рассмотрено.

Осталось показать оптимальность для подзадач при расчете каждой из 3 частей.

Рассмотрим в качестве примера часть 2. Предположим, что в состоянии ( y + t_j + s₁ , s + 2 ) последним был взят элемент j . Если состояние ( y, s ) не оптимальное, то можно взять другие элементы, улучшив решение для состояния ( y + t_j + s₁, s + 2 ), при этом не нарушив остальные ограничения. Следовательно, подзадача в данном случае оптимальна, и это означает, что алгоритм находит оптимальное решение.

Заметим, что в случае присутствия ограничений (3)–(5) указанный алгоритм не будет работать, поскольку появляется зависимость расчета 3 частей от взятых элементов, следовательно, необходимо организовать перебор всех допустимых по ограничениям (4), (5) подмножеств элементов, а уже при выбранном подмножестве выполнить указанный алгоритм.

Теорема 2. Сложность алгоритма O(N²L²S² + L³S³), где L – количество возможных позиций y_p (в случае вещественных позиций умножаем, чтобы получить целые части), S = max { M s , M^{s 2} } .

Доказательство.

В работе алгоритма на самом верхнем уровне осуществляется перебор всех возможных Wb, а поскольку их количество ограничено N, следовательно, в оценке получаем первый сомножитель N. Далее шаги по расчету динамики для части 1 добавляют в сложности LSN на каждой итерации перебора Wb в силу того, что состояний в динамическом программировании LS, а на переход необходимо N итераций. Аналогично шаги по расчету части 3 занимают LSN операций. После этого перебираются все возможные состояния (yc, sc), что занимает LS операций. Для каждой итерации необходим расчет части 2, что по аналогии с частью 1 и 3 занимает LSN итераций, и в конце работы необходим перебор состояний из частей 2 и 3, что занимает L2S2 операций, в результате: O (N2L2S2 + L3S3).

Заметим, что на практике алгоритм работает быстрее в силу следующих факторов:

• •    не все состояния достижимы;           _W b

• •    при расчете ч. 3 состояния начинаются с ;

• •    чаще всего множество позиций – просто целые числа, поскольку параметры t_j и w_j представляют собой целые числа в миллиметрах (редко миллиметры с десятыми долями).

Система реализована средствами Microsoft Visual Studio 2012 и прошла опытную эксплуатацию на Соломенском лесозаводе (г. Петрозаводск), где она продемонстрировала экономический эффект 400–700 тыс. руб. в месяц.

• *    Работа выполняется при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

MATHEMATICAL MODELS AND GEOMETRICAL FEATURES OF WOOD SAWING IN PLANNING AND MANAGEMENT OF SAWMILL INDUSTRY