Математические модели развития обслуживания объектов морской техники

Цель настоящей работы – показать взаимосвязь между совокупностью параметров морских инженерных сооружений (МИС – типа буровых платформ) и их экономической эффективностью; получить прогнозную оценку различных стратегий развития технических и эксплуатационных параметров МИС (совокупных параметров системы).

В настоящее время с освоением Мирового океана связывают решение четырех основных проблем, имеющих первостепенное значение для дальнейшего развития общества: увеличение добычи минерального сырья, использование энергии океана, обеспечение продуктами питания и размещение населения [7]. Шельф, как самая доступная часть Мирового океана, служит зоной активной деятельности человека по освоению минеральных, биологических и химических ресурсов за пределами суши.

Существуют следующие основные направления использования континентального шельфа:

• •    освоение шельфа как источника нефти и газа;

• •    освоение шельфа как источника твердых полезных ископаемых;

• •    освоение шельфа как источника биологических ресурсов;

• •    освоение шельфа как источника энергии;

• •    использование шельфа для размещения на нем гражданских и про-

• мышленных объектов.

Среди указанных направлений достаточно большой интерес в настоящее время представляет шельф как источник нефти и газа. Установлено, что общая нефтегазоносная площадь континентального шельфа составляет около 13 млн. км2, а суммарные запасы нефти – около 100 млрд. т [7].

Ощущая нехватку энергетических ресурсов, многие страны мира ведут поисковые и добычные работы в пределах морских акваторий. В начале 70-х гг. XX века 21 государство добывало нефть и газ в океанах и морях, 46 стран проводили геофизические и буровые работы, 5 стран готовились к ним. В начале 90-х гг. поиском морских месторождений и их разработкой занималось уже более 100 государств. В настоящее время освоение ресурсов шельфа, несмотря на сложные природно-климатические условия морского поиска, непрерывно продолжается. Разведка месторождений осложняется штормовыми ветрами, наличием мощной толщи воды, волн, сильных течений и айсбергов. Все это увеличивает затраты на поиск и добычу морских углеводородов.

Тем не менее, добыча нефти в море неуклонно растет, составляя в среднем 32 % общемировой, так как потенциальные ресурсы нефти и газа в акваториях Мирового океана превосходят их запасы на суше почти в 3 раза. От- крытия начала 90-х гг. подтвердили более 500 месторождений у берегов США, более 150 – в Северном море и свыше 40 – в Персидском заливе [7].

Стоимость строительства морских скважин достаточно высока. Например, средняя стоимость 1300 поисковых, разведочных и эксплуатационных скважин, пробуренных в Северном море, составила 2,5 – 5 млн. долл. При разработке месторождений Арктического региона эта стоимость возрастает на порядок. Суммарные затраты в мире за период с начала 70-х до середины 80-х гг. составили более 600 млрд. долл., из которых 265 млрд. долл. истрачено на поисково-разведочные работы и добычу нефти.

Прибыль на каждую тонну добытой нефти резко снижается с глубиной воды в точке бурения скважины. Например, если на суше она в среднем составляет 3,65 долл., то на глубине 3 м – 2,41 долл., 30 м – 1,68 долл., 130 м – 0,66 долл. Доходы от добычи газа падают до нуля даже при 3-метровой глубине моря. Подсчитано, что пределом рентабельности разработки месторождения сегодня является глубина моря 100 м для месторождения с запасами нефти 7 млн. т и 130 м для месторождений с запасами 13,5 млн. т нефти. Несмотря на высокие капиталовложения, поиск и разведка новых месторождений нефти и газа ведутся во все более широких масштабах, и распространяются на глубоководные районы шельфа, поскольку свыше 30 % запасов нефти и газа в Мировом океане находится за пределами зоны с изобатой 200 м. Наибольшая доля всех объемов капиталовложений на освоение шельфа приходится на разведку и освоение месторождений нефти и газа [7].

Анализ состояния проблемы освоения Мирового океана в настоящее время показывает, что создание морских инженерных сооружений на континентальном шельфе, как и любых других технических объектов, не является самоцелью: оно обусловлено общественно необходимыми потребностями. Для большинства стран с развитой ка- питалистической экономикой проблема освоения ресурсов континентального шельфа является своего рода «двигателем», т. к. естественной основой существования и развития являются рационально построенные механизмы стимуляции общественного потребления. Особенно важно это обстоятельство для европейских и скандинавских государств, где запасы полезных ископаемых – энергоисточников потребления – на суше находятся на грани исчерпания, а их добыча на территориях колоний все больше осложняется наличием социальных проблем. Поэтому естественным выходом из этой ситуации представляется возможность осваивать ресурсы шельфа, тем более что по ряду прогнозов и оценок запасы последних достаточно велики.

Важным элементом удовлетворения потребности общества в ресурсах шельфа, таким образом, являются технические инженерные сооружения – буровые установки различных типов; причем достаточно большой удельный вес занимают стационарные буровые установки [7].

Очевидно, что проектирование любого нового объекта морской техники необходимо начинать с анализа существующих и потенциальных потребностей общества, точнее, той его части, которая будет покупать и использовать этот объект, а также с оценки состояния объекта морской техники и прогнозирования потребности общества на определенный период времени, с тем чтобы обеспечить достаточный временной интервал для создания объекта морской техники с теми свойствами, которые потребуются от него через некоторое время. Последнее обстоятельство особенно существенно, если учесть, что период постройки большинства морских инженерных сооружений соизмерим с возможным временным интервалом прогноза.

Необходимость освоения ресурсов шельфа, обоснованная выше, толкнула развитые страны на путь создания качественно новых объектов морской техники – технических средств освое- ния ресурсов, среди которых значительный интерес представляют стационарные буровые платформы. Развитие таких средств приходится в основном на период с 1960 по 1990 гг., когда экономика государств, о которых идет речь, в целях совершенствования переходит к новым технологиям, стимулирующим общественное потребление, к развитию новых, наукоемких форм маркетинга и внутрифирменного планирования производства. Такие формы деятельности всех промышленно-производственных фирм являются залогом их успеха на данном сегменте рынка, а в основе всех форм и методов планирования производства, менеджмента и коммерческого маркетинга лежат научные способы изучения и прогнозирования технологических характеристик производимых технических систем, а также выявление объективных законов их развития. В основе исследования указанной проблемы должен лежать математический аппарат нелинейного моделирования [1]: формирование самой математической модели развития, методы определения параметров модели (главным образом, метод наименьших квадратов) и верификация получаемой таким образом модели.

Рассмотрим возможность создания математической модели на примере развития тенденции к увеличению возможности стационарной буровой платформы эффективно работать на больших глубинах моря. Обозначим изменение глубины производства работ во времени как некоторую функциональную характеристику развития [1]:

y = y ( t ) , (1)

где t – время.

Под величиной « y » можно понимать также другие техникоэксплуатационные показатели стационарной буровой платформы: объем максимальной суточной добычи нефти, высоту опорных колонн для платформ на свайном основании со сквозным опорным блоком, площадь опирания на грунт и пр.

C течением времени рост «y» ограничивается теоретическим пределом каждой стадии развития, поэтому необходима модель в виде нелинейного дифференциального уравнения, которое можно аппроксимировать степенным многочленом [1]:

dy = a i ⁽ t )• y + a 2 ⁽ t )• y ² + ... + a_n ⁽ t )• yⁿ .

dt

В качестве первоначальной модели рассмотрим квадратичное приближение: a , ( t ) = 0, при i >3 , адекватно отражающее все основные особенности и характеристики этого процесса:

dy = a i ⁽ t )• y + a 2 ⁽ t )• y ² , a_o(O = 0.

dt

Это уравнение является уравнением Бернулли, которое проинтегрируем, введя новую зависимую перемен- 1

ную:     y .

В соответствии с указанными условиями «z» удовлетворяет уравнению:

dz

— = aQ_x ( t ) • z — a^ ( t ) .

dt       ^{1           2}

Будем искать решение уравнения в виде произведения функций от «t»:

z ⁽ t ) = z i ⁽ t )• z 2 ⁽ t ) .

Дифференцируя обе части равенства, находим:

этого двух

этого

dz      dz1

= z     +z1

dt       dtdt

.

Подставив (4) и (5) в (3), получим:

dzdz z 2    - + zi    - = -ai(t )• zi-z 2-a 2(t), dtdt

--h a₃ (t) • z₇ + z₇--= at ^{y 2} 7      ² at

-a2(t)

Выберем функцию z2 (t) такой, dz чтобы:     —- + a, (t )• z2 = 0,     тогда:

dt ^{1       2}

-^- = -a ] ( t ) • dt . Интегрируя, получаем: z ₂

• a , ( t )• dt

• - 2 ( t ) = C i e ¹       .         (6)

Не пренебрегая общностью, можно положить произвольную постоянную C1 равной единице. Для определения z1(t) имеем теперь уравнение:

dz		dz	a 2 ( t )
z 2 ( )            a 2 ( ), dt		dt	Z 2 ( t )

Отсюда:

z , ₍ t ) =   ^a₂⁽y __d+_c .     ₍₇)

• ¹              Z 2 ( t )•

где C - постоянная интегрирования.

Подставив выражения (6) и (7) в (4), найдем:

• a. (t)• dt z (t )• = C-e-...

• a . ( t )• dt                    a. ( t )• dt

...- e           Ja2 (t )• e         .(

Таким образом, получена функ- циональная зависимость исследуемого параметра МИС от времени:

y (t) =C e

..- e

I a , ( t )• dt

J a 2 ( t )

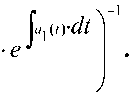
Это выражение представляет собой аналитическую зависимость науч- но-технического развития эксплуатаци- онных и конструктивных параметров стационарных буровых платформ.

Положим в выражении (9): a2(t) = 0      ; ax(t) = Ь-^'‘, где b и к - постоянные. Получим:

y(t) = C.e-^bekt ,      (10)

где: С = —; b = -b ; к = -к .

С     к

Выражение (10) представляет собой функцию Гомперца [1]. Из соотношения (9) можно получить также и выражение для функции Перла [1], если положить: a 1 (t ) = к 1 ; a ₂( t ) = к ₂, т.е. считать коэффициенты постоянными.

В этом случае получим:

W) =   ^L— .      (11)

• 1    + a-e

где: L=-k 1 / к ₂; a=C -к 1 / к ₂; b=k 1 . Зависимость (11) представляет собой функцию Перла.

Положим теперь в выражении (9): a_x (t ) = k_x•e^k'^t ; a₂^k₂•e^k•^t .

В этом случае получим [1]:

-y ( t ) =     L -e t .               (12)

be a+e где: L = 1/C; a = - к2/(C -к — -к); b = - к1/к ; P=- к.

Выражение (12) - определяет S-функцию. С помощью этой функции можно более гибко аппроксимировать статистические данные (ниже будут приведены примеры построения модели изменения высоты опорных колонн для платформ на свайном основании со сквозным опорным блоком и модели изменения площади опирания на грунт для гравитационных железобетонных платформ по статистическим данным, приведенным в таблицах 1 и 2), чем с помощью кривых Перла и Гомперца, так как она включает большее количество коэффициентов [6]. Несмотря на то, что с помощью выражения (9) решение поставленной задачи можно получать с любой степенью точности, введение числа постоянных величин более четырех непропорционально усложняет расчеты и поэтому в большинстве случаев вряд ли целесообразно [1].

Следующим шагом на пути решения задачи является вычисление параметров L . a . b . |3 по имеющейся совокупности статистических данных существующих буровых платформ заданного типа. В качестве таких данных могут быть: глубина моря в районе работ (за определенный период времени), объем максимальной суточной добычи нефти, высота опорных колонн, площадь опирания на грунт (для гравитационных железобетонных платформ) и пр.

Физический смысл постоянных коэффициентов в функции (12) определяется тремя величинами: L, a, b , которые выражают постоянное начальное значение функции (12) при t = 0, а величины L и а дают возможность найти ее предельное значение, когда t —> +со. Коэффициент , измеряемый в единицах, обратных единицам времени (чаще - годам), является постоянной времени экспоненты. Коэффициент b - безразмерная величина; отношение L/a имеет размерность функции y(t).

В качестве подтверждения работоспособности рассмотренной выше модели приведем сравнение изменения высоты опорных колонн для платформ на свайном основании со сквозным опорным блоком за период с 1965 по 1995 гг. (рис. 1) и изменения площади опирания на грунт для гравитационных железобетонных платформ за период с 1970 по 1990 гг. (рис. 2).

Таблица 1 – Высота опорных колонн для стационарных платформ на свайном основании [4, 8, 9, 10]

№ п/п	Год постройки платформы	Высота опорных колонн, м
1	1967	37
2	1969	44
3	1970	27
4	1971	94
5	1976	230
6	1981	340

Таблица 2 – Площадь опирания на грунт

для гравитационных железобетонных

платф	орм [2, 3, 5]
№ п/п	Год постройки платформы	Площадь опирания на грунт, м 2
1	1975	6350
2	1976	8220
3	1977	9815
4	1981	18000
5	1983	8550
6	1984	13000

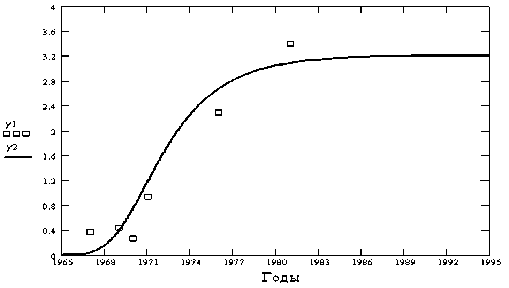
Рисунок 1 – Распределение высот опорных колонн построенных платформ (статистический материал таблицы 1): - S -функция.

На процесс развития любого объекта техники во времени одновременно влияют совокупности прогрессивных и регрессивных факторов. Начало эволюционной фазы характеризуется зарождением идеи новой техники, созданием ее первых образцов [6]. При этом наблюдается постепенный рост ее функциональных характеристик: внача- ле эта скорость роста небольшая, но постепенно она увеличивается. Этот процесс можно представить в виде следующего графика [6]:

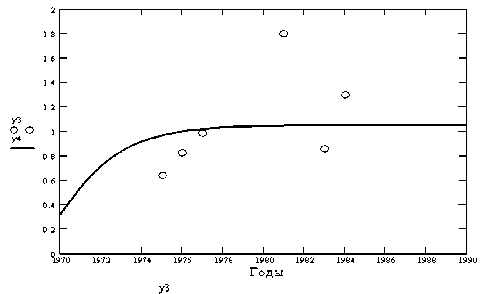
опирания на грунт построенных платформ гравитационного типа (статистиче-у4

ский материал таблицы 2):       – S -

Рисунок 2 – о о – распределение площади функция.

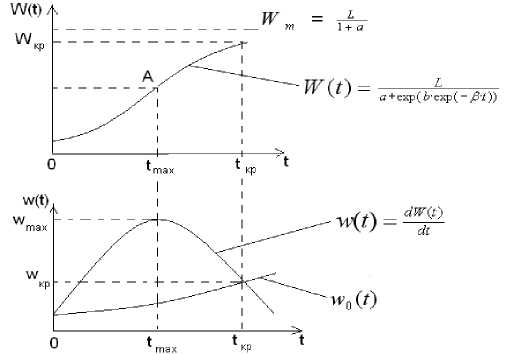
Рисунок 3 – Схема процесса развития объекта техники

В период времени от 0 до t max преобладает действие прогрессивных факторов (научные идеи, технические достижения). Однако постепенно эти темпы начинают замедляться, и после точки перегиба (точка A, рис. 3) начинается непрерывное снижение скорости приращения параметров и асимптотическое приближение к некоторому пределу, обусловленному действием объективных законов природы.

Дальнейший рост количественных параметров возможен только в результате качественного скачка (революции). Для технических средств – это переход к использованию новых физи- ческих явлений, новых видов энергии, новых конструкционных материалов [1].

Можно показать, что эволюционная фаза характеризуется созданием на основе базового варианта различных модификаций и модернизированных образцов. Необходимость таких изменений базового образца обусловлена стремлением увеличить функциональные параметры (правда, на сравнительно небольшую величину) при малых затратах времени и ресурсов; расширить целевое назначение; изменить целевое назначение. Кратность таких модификаций, как, впрочем, и время их существования, обуславливаются общественно необходимыми потребностями [1].

Таким образом, любой объект морской техники можно рассматривать как непрерывно развивающийся и совершенствующийся, причем это развитие находится под воздействием объективных законов. Ввиду наличия значительных интересов развитых государств в вопросах освоения ресурсов шельфа, проблемы построения и изучения моделей развития технических систем, обеспечивающих это освоение, представляются достаточно важными. Ведь величина прогнозной оценки часто совпадает с временным интервалом, необходимым для постройки самого сооружения, что может быть использовано в планировании.

Таким образом, в работе представлена динамическая математическая модель получения соответствующих прогнозных оценок. Эта модель основана на дифференциальном уравнении, описывающем изменение основных параметров МИС с течением времени. В качестве начальных приближений решения этого уравнения могут быть использованы логистические функции – функции Перла, Гомперца и S-функция.