Математические модели траекторий движения узлов машин с микрошероховатыми составляющими среды

необходимо выбрать критерии оценок. Будем считать, что в системе координат У1 поверхность Ф1 неподвижна, поэтому требуется найти закон движения Ф2 в У2, обусловленный перемещением и поворотом деталей размерной цепи. Положение твердого тела в пространстве определяется девятью координатами трех точек не принадлежащих одной прямой.

Уравнение движения точки М принадлежащей поверхности Ф4 в системе координат У1 имеют вид x = f i (xm , Ут , zm , t)

У = f 2 (xm , Ут , zm , t); z = f 3 (xm , ym , zm , t), где x, y, z – координаты точки М поверхности Ф4 в системе координат У1; xm, ym, zm – подобные координаты в системе У4; t – параметр времени.

В векторной форме (1) записывается r = ^f ( r m , t^).                    (2)

Так как система координат У4 перемещается относительно У1, то записывают закон их относительного движения.

На рис. 2а представлена совокупность систем координат эквивалентной схемы размерной цепи машины, где система координат У3 неподвижна.

Запишем уравнение для радиусов-векторов, связывающих начала координат

R = r02+ r01+ r ,

R = r04+ rm .(4)

Из соотношений (3.) и (4.) следует.

r = r04 + rm - r02 - r01.(5)

Полученное выражение показывает, какие радиус-векторы оказывают влияние на положение точки М в системе У_3. Найдем положение точки М последовательно в системах координат У 3, У 2 и У 1.

В системах У₃ и У₄ точка М определяется радиус - вектором R

R = r 04 + Р 4 r m ,             (6)

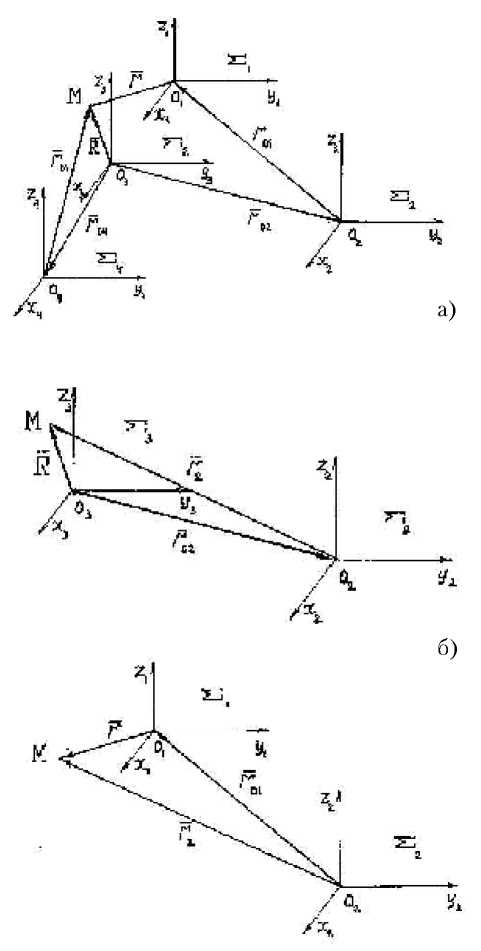
в)

Рис. 2. Совокупность систем координат где Р4 – матрица поворота системы У4 относительно У3 .

Положение точки М в системе координат У2 (рис. 2б) устанавливается

R = r₀₂+ Р₂ r₂ .               (7)

Отсюда r2 = Р2-1(R-r02) .              (8)

Здесь Р₂ и Р₂^-1 – матрица поворота системы У₂ относительно У₃ и обратная ей. Определим радиус-вектор r положение точки М в системе координат У₁ (рис..2.в) считая, что в системе У₁ r₂ = r₀₁ + Р₁ r .

Тогда

Р₁ r = r₂ - r₀₁                (9)

Подставим (9.) в выражение (8.)

Р 1 r = Р 2 ^-1 (R - r 02 ) - r 01 .

Преобразуем полученный результат с помощью (7.) в

Р₁ r = Р₂^-1 ( Р₄ r_m + r₀₄ – r₀₂) - r_{01 ,}

Окончательно r = Р1-1 [Р2-1 (Р4 rm - r04 - r02 ) - r01] .    (10)

Таким образом, в соотношении (10) учтены любые перемещения и повороты систем координат связанных со звеньями размерных цепей. Следует отметить, что при выводе уравнений движения рабочей поверхности необходимо учитывать:

геометрические отклонения от номинально заданных параметров; нарушение кинематических связей; влияние факторов, порождающих геометрические погрешности;

силовые воздействия;

тепловые факторы;

вибрации;

изнашивание;

остаточные напряжения;

влияния смазки в кинематических парах, работающих в условиях смешанного трения их микрошероховатых поверхностей.

В общем случае влияние контактной жесткости и смазки в стыках на упругие перемещения достигает в общем балансе порядка 40 ÷ 80%. Поэтому при расчете показателей точности устанавливается связь между непосредственными или косвенными характеристиками реальных процессов теоретически с помощью адекватных математических моделей или экспериментально.

При синтезе механизмов и машин необходимо в расчетах учитывать влияние смазки на взаимное расположение микрошероховатых поверхностей скольжения кинематических пар работающих в условиях граничной смазки. Указанные микронеровности образуются в результате различных способов обработки поверхностей и в процессе соприкосновения между ними образуются лабиринты макро- и микрощелей, заполненных движущейся смазкой. Уравнение ее фильтрации в декартовой системе координат для различных областей имеет вид (11)

∂   hk ∂ P  ∂   hk ∂ P

” ^(р --~) +7" ^{( р} --"Г") +

∂x  η ∂x  ∂y  η ∂y д  hk дР  d      д hp2

■_ Р • ^) = ( P Л h ) +т (    ^Р х ) +

∂ z   η ∂ z   dt      ∂ x η ₍₁₁₎

+1(hJP р-)+! (h^- Pz),

∂y η    ∂z η где величины Px, Ру, Pz массовые силы движущейся жидкости k,Λ функции пористости и проницаемости сопряжения шероховатых поверхностей, ρ,η - плотность и динамическая вязкость смазки.

ЗАКЛЮЧЕНИЕ

Точность относительного расположения и движения исполнительных поверхностей звеньев машин со временем нарушается, поэтому возникает проблема достижения и сохранения заданного уровня нормативных показателей точности как при изготовлении машины, так и в процессе ее эксплуатации. Для устранения данной проблемы требуется решение следующих основных задач:

• -    совершенствование конструкций механизмов и машин;

• -    подавление факторов, порождающих погрешности;

• -    управление процессом образования погрешностей.

Первые две задачи являются традиционными в расчетах машиностроения, третья успешно развивается в результате разработки и внедрении систем автоматического регулирования (САР). Для решения каждой из вышеуказанных задач необходимо получение точной информации о фактических погрешностях. Ее источником выступают количественные параметры, не- посредственно или косвенно характеризующие положение поверхности в соответствующих системах координат. В связи с этим уравнения относительного движения контактирующих поверхностей должны содержать функциональные зависимости и количественные характеристики, связывающие внешние возмущения и порождаемые ими погрешности в положении кинематических пар.

Авторами предложены аналитические зависимости, полученные в результате решения уравнения (11) и достоверно описывающие физические процессы в машинах между звеньями и их кинематическими парами. Данные зависимости могут быть использованы для построения математических моделей относительного движения и расположения рабочих поверхностей деталей машин, учитывающих влияния воздействующих факторов на погрешность их расчетных траекторий. Использование математических моделей и аналитических зависимостей позволит достичь итогового обеспечения точности функционирования технологического оборудования.

Работа выполнена при поддержке гранта по ведущим научным школам РФ 2008-2009 гг. (НШ-4245.2008.8) и в рамках программы “Развитие научного потенциала Высшей школы” Минобрнауки РФ

MATHEMATICAL MODELS OF TRAJECTORIES OF MOVEMENT OF UNITS OF MACHINES WITH MICRO-ROUGH COMPOUNDS OF MEDIUM

• ¹    Togliatti State University

• ²    Samara State Technical University