Математические модели в задачах синтеза плоских оптических элементов

В работе рассматриваются следующие обратные задачи синтеза оптических элементов:

Задача 1. Формирование заданного изображения в заданной плоскости.

Задача 2. Формирование заданной диаграмма направленности.

Задача 3. Задача фокусировки электромагнитного излучения в заданную кривую.

Задача 4. Создание плоских оптических элементов на основе дифракционных решеток (ответвители, делители пучка).

Охарактеризуем те математические проблемы, которые возникают при решении перечисленных задач синтеза. С математической точки зрения все эти задачи сводятся к решению операторного уравнения

А<р = F.                                                                            (1)

Здесь F - характеристики изображения, <р - характеристики оптического элемента, реализующего изображение с характеристиками F. Оператор А в выбранной математической модели осуществляет соответствие между ср и F (ср и F - элементы некоторого функционального, для определенности нормированного пространства).

Проблема 1. Проблема выбора математической модели.

С одной стороны, модель должна быть достаточно простой, с другой -она должна с требуемой точностью отвечать реальным процессам, происходящим в оптической системе.

Проблема 2. Проблема разрешимости задачи синтеза.

Задача синтеза (1) разрешима, если для любого F найдется элемент Ф€0, такой, что inf I I Аср - FI I = О

Ф 6Q

Здесь Q - множество возможных реализаций. На самом деле необходимо реализовать элемент Фе, который с заданной точностью е решает задачу синтеза, то есть I |Аф£ - FII < е. В этом случае будем говорить об е-раз-решимости задачи синтеза.

Проблема 3. Проблема единственности решения задачи синтеза.

Отметим сразу, что в большинстве случаев рассматриваемые задачи синтеза имеют неединственное решение. Однако, в отличие от задач диагностики, неединственность решения в задачах синтеза играет в каком-то смысле положительную роль: ее можно использовать для оптимизации дополнительных характеристик элементов.

Проблема 4. Проблема создания эффективных алгоритмов решения обратных задач синтеза оптических элементов.

Здесь необходимо отметить, что требуется построить устойчивые алгоритмы, с заданной точностью решающие задачи синтеза.

Проблема 5. Создание программно-аппаратных средств для решения задач автоматизированного проектирования оптических элементов.

Математические модели в задачах синтеза оптических элементов Приближение Френеля.

Одной из наиболее распространенных моделей в задачах синтеза оптических элементов является приближение Френеля. В этом приближении распространение излучения в вакууме описывается волновой функцией

U(x, у, z, t) = u(x, у, z) е-1®^

Здесь u(x, у, z) - комплексное волновое поле, удовлетворяющее уравнению Гельмгольца

Ди + к2и = 0.

Пусть плоский оптический элемент расположен в плоскости z = 0 и u(g, Пг 0 - 0) - комплексное волновое поле падающего излучения в плоскости z = 0. Пусть и(Е, п, 0 + 0) - волновое поле на выходе плоского оптического элемента. Не уменьшая общности, будем считать, что плоский оптический элемент перпендикулярен падающей волне (рис. 1) (например, падающее излучение - плоская электромагнитная волна, распространяющаяся вдоль оси z) . В приближении плоского элемента комплексная волновая функция и(£, п, 0 + 0) на выходе элемента связана с полем и(Е, п, 0-0) соотношением

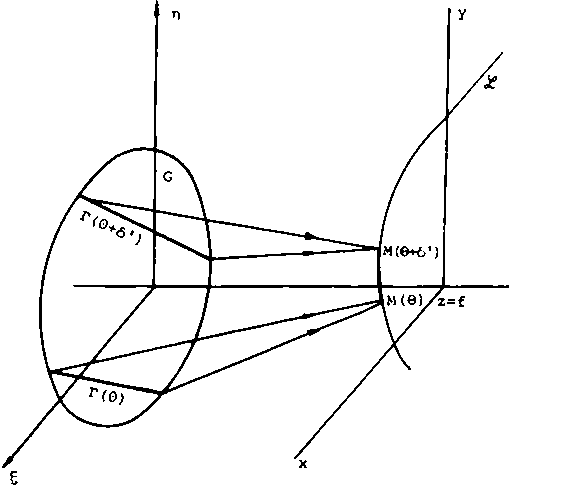
Рис. 1. Геометрия расположения плоского оптического элемента и области формирования изображения (задачи 1, 3)

и(Е/ п, 0 + 0) = и(Е, п, 0 - 0) С(Е, п).                             (2)

В (2) С(Е, п) - комплексная функция пропускания элемента. Если |С(Е, п) I = 1 в области G, то элемент является фазовым. Если Im С(Е, и) = 0 в G, то элемент называется амплитудным. Из соотношения (1) следует, что, зная п(Е, и, 0 - 0) и и(Е, п, 0+0), можно (если это допускает соотношение (2)) найти пропускную способность С(Е, и) и изготовить оптический элемент, решающий задачу синтеза [1]. Таким образом, проблема сводится к расчету комплексного волнового поля и(Е, п, 0+0) сразу за оптическим элементом, решающим задачу синтеза. Пусть и(Е, п, 0 + 0) = А(Е, п) 6 ^^(Е'В) . здесь А (Е, п) - действительная функция. В приближении Френеля модуль комплексного волнового поля и(х, у, f) в плоскости z = f находим как ik(^ + p) iki^ni

|u(x, У, f) | = |^ n e ^{1     £} e ^2£

. A(E, n) eik(p^,n^dE dnl = B(x, y) .                             (3)

В задаче синтеза (1) задана функция В(х, у) и требуется найти функции А(Е, и), <Р(Ег И) из соотношения (3) . Если пару функций А, щ обозна- чить за Ф, то соотношение (3) можно переписать в операторном виде

Т Ф = В.                                                                     (4)

Если оптический элемент фазовый, то А(Е, п) известна и неизвестной является лишь функция <р(Е, п) •

Задача 2 - задача формирования диаграммы направленности - на самом деле сводится к задаче 1. Рассмотрим формулу (3) в приближении, что f - «° так, что j = а; ^ = 0.

• eik(5a+nB) d£ dnl = R(a, B).

Функция R(a, В) зависит лишь от a и В и является амплитудной диаграммой направленности оптического элемента. Ясно, что задачи (1) и (2) связаны между собой. Так, если функции А(Е, п) и ср(Е, п) решают задачу (1>, то функции А(Е, и) и

Ф(Е» п) = Ф(Е» П) + ^₂р                                           (6)

решают задачу формирования диаграммы направленности с К(а,В) = lim |fu(af, Bf, f) I • Ясно, что ср отличается от ср добавлением в оптиче-скую систему линзы с фокусным расстоянием f.

Теорема о разрешимости задач синтеза 1, 2

Пусть в(х, у) - заданная функция, суммируемая с квадратом в области G. Обозначим через Л (А, ср)

Д (А, ф) = //[Ё(х, у) - | и (х, у, f) | }2 dx dy.                          (7)

Интегрирование ведется по всей плоскости z = f. Справедлива теорема 1.

Теорема 1. Существуют такие функции В(х, у), «суммируемые с квадратом на плоскости, что in f Д (А, ср) = До > 0.

Ф, А

Замечание" 1. Последнее означает, что задача синтеза оптических элементов, формирующих в плоскости z = f заданное изображение, разрешима далеко не всегда даже в рамках амплитудно-фазовых оптических элементов, а тем более для фазовых оптических элементов. Можно построить оценку снизу для величины До, которая будет характеризовать тот уровень приближения, лучше которого в принципе нельзя сформировать заданное изображение F. Те же результаты относятся к задаче 2.

Замечание 2. Примером такой функции является любая разрывная функция, например:■

I 1, x2 + у2 < R2

в (х,у) = О, X2 + у2 > R2.

Можно показать, что при падении плоской монохроматической волны на оптический элемент (п(Е, П, z) = С ^lkz) фокусное расстояние f -50 см, круглая апертура -1 см, диаметр изображения -1 см и X = 10.6ц, величина △ составляет в процентном отношении 1-2%.

Алгоритмы решения задач 1, 2 в рамках приближения Френеля

Все существующие алгоритмы решения задач 1, 2 в рамках приближения Френеля так или иначе сводятся к задаче минимизации функционала невязки

Д(А, ф) = //(В(х,у) - |и(х, у, f)|}2 dx dy.

Обычно [2] используются различные итерационные алгоритмы. Отметим сразу, что оператор Т в соотношении (4) нелинейно зависит от А и ф, поэтому задача минимизации функционала Д(А, ф) - задача невыпуклого программирования. Построение итерационных алгоритмов, гарантирующих сходимость к точке минимума функционала Д(А, ф) - задача чрезвычайно сложная.

В настоящее время в литературе по оптике широкое распространение получили итерационные алгоритмы, предложенные в работе [з]. Введем обозначения v(E, n) = А(Е, n) eikt₽^/T1\ Тогда ik^2     ik^

u(x, у, f) = Уо е         У(у(Е, п) е         ).                     (8)

Здесь ^ - двумерное Фурье-преобразование от аргумента, Yo - постоянный коэффициент. Таким образом, для построения последовательности, минимизирующей функционал Д(А, ф) , можно использовать хорошо разработанную технику Фурье-методов (быстрого Фурье-преобразования, спецпроцессоры и т.п.). Не уменьшая общности, можно считать, что задачи 1, 2 для фазо вых элементов сводятся к решению следующей математической проблемы. Пусть две функции u(E,n), v(E, и) связаны соотношением u = Ф v, причем известны |и(Е, и)I = В(Е, п) и |v(E, и)I = А(Е, и)• Задача заключается в том, чтобы найти фазу одной из функций, например и(Е, п)• Алгоритм, предложенный в работе, является по сути дела алгоритмом простой итерации для минимизации функционала Д(А, ф) и заключается в следующем. Пусть на k-м шаге алгоритма ик(Е

И) найдена. Тогда вычислим и£+^ по следующему правилу: фаза функции и, приписывается амплитуде В(Е, п), то есть uk

Uk+1^' n) = [и | B^' n^ • ТепеРь vk+i =^~uk+i* фУнкЦия vk+1 находится тем же способом: и т.п.

к+1 = Т^Т А(Х' у)* И' наконец' uk+l =yvk+l

Для алгоритмов подобного типа доказано, что они являются релаксационными, то есть невязка I |а - |v, | ||² является монотонной функцией от итерации к. Заметим, что это вовсе не означает, что последовательность и_к, построенная по этому алгоритму, является сходящейся.

Для минимизации функционала А (А, <р) можно использовать и традиционные алгоритмы, например метод наискорейшего спуска и т.п. Вычисление градиента функционала А(А, ф) не представляет сложности.

Отметим, что для оптического диапазона, как правило, очень хорошим приближением является приближение геометрической оптики [4] . Приближение Френеля лишь незначительно улучшает результаты, полученные в приближении геометрической оптики. Так, для характерной геометрии: диаметр G *1 см, диаметр изображения ~1 см, X = 10,6ц, f ~50 см, функционал невязки А(А, ф) с начального приближения, получаемого в рамках геометрической оптики, удается улучшить обычно лишь в 1,2+1,5 раза.

Математические модели в обратных задачах синтеза оптических элементов.Приближение геометрической оптики

Приближение геометрической оптики можно получить из формулы Френеля keikf             [k^ll + ^znll » ф(Е,п)]

u(x, у, f) = -™— И а(Е, п) е 2f 2f          dE dn к 1 G при к - ”.

Простейший случай, когда для каждой точки (х, у) из некоторой области D, где формируется изображение, существует лишь одна стационарная точка (Ео. По)г являющаяся решением уравнения стационарной фазы

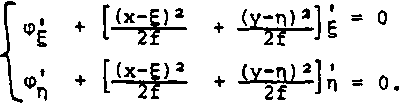
Система (9) определяет отображение области G плоскости О ЕП на плоскость z = f (рис. 2):

I ; fX=E + f»E

Ф \ У = П + f Ф^

Обозначим за 11 1^,11 матрицу

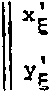
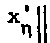
УП

Нетрудно убедиться, что при

" и(х, у, f) имеет асимптотику и (х,

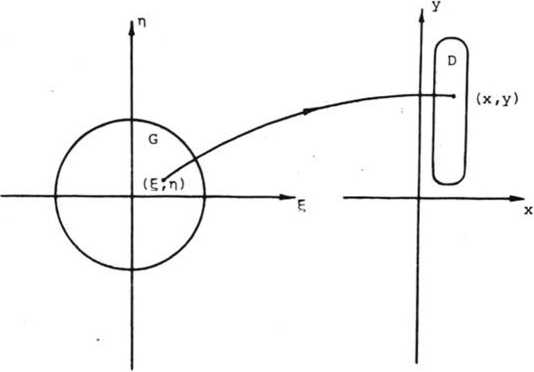
Рис. 2. К постановке задачи 1 в рамках геометрической оптики

у, f) = А(Ео, По)

Э(^х' У ) э(5, л)

о(4^)

Здесь —|^—^у - якобиан преобразования (10), взятый в точке (Ео,Ло). Теперь задачу синтеза (1) можно в рамках геометрической оптики переформулировать в следующем виде. Требуется найти взаимооднозначные отображения I: х = х(Е, И) ; У = у(5, л) , удовлетворяющие условиям: IG=D,причем •                 t хл = у5?

1^Х5 ^ул ' ^хл ^УЁ1 = 9о<Е, л).

Здесь д0(Е, Л) - заданная функция, определенная интенсивностями падающего и создаваемого изображений.

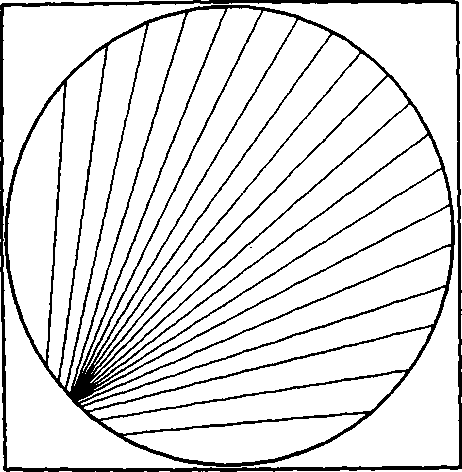
Пусть теперь решение уравнения (9) неединственно.Этот случай соответствует наличию фокусировки излучения. Рассмотрим задачу фокусировки (задача 3) в фокальную кривую L : х = х₀(0), у = уо(0), z = f, 0 - натуральный параметр. Будем считать, что для каждой точки (х_о(0), у₀(0), f)eL множество точек стационарной фазы (решение уравнения (9)) есть гладкая кривая Г (x_q (0) , у₀ (0)) = Г(0), а для точек (х, у, fJ^L Г(6)=<3.

Справедлива теорема 2 (необходимое условие фокусировки)[5]. Пусть I G = L, a rang || I , || = 1 везде в области G (G - строго выпуклое множество). Тогда Г(0) - отрезок кривой с нормалью {x_Q(e)_} у (е)}. Последняя теорема существенно упрощает решение обратной задачи синтеза в рамках приближения геометрической оптики.

Для поля на кривой (х, у, f)eL можно получить асимптотику при к - 00

u(x, у, f) =^

ik(f+S0) i-r A(E,n)dl

e 4 /              --:

r(0) \|Sp|| I ,|||

+ о ( /к ) .

(11')

Здесь Sp || • || след матрицы || • || . Видно, что при к - 00 амплитуда по ля на кривой стремится к бесконечности. Для амплитуды поля вне кривой (исключая концы) можно получить представление

с(х, у)      , 1 .

и(х, у, f) = — -   + о (---) .

/к /к

Пусть в точке х0 = 0, у о = 0 кривая X имеет касательную - ось 0Y. Рассмотрим поле и(х, 0, f) на оси ОХ. В реальном эксперименте измеряется усредненная по некоторому отрезку интенсивность 6

^асл” { |и(х, 0, f)|=dx. —о

Справедлива теорема 3. При к •• * величина I , имеет асимп- набл тотиху

A2(E,n)dl

1на6л ”г(е) Ы1 т^, (е,п) II I + °(1> *                               (12)

Результат теоремы можно переформулировать следующим образом (см. рис. 1).

АТ      П      A2(E,n) dg dn +

1ф (М(0)М(0+6'))

(0) + о(1) .

I = lira

НдоЛ с । а о

+ 0(1) = Рх ф

Таким образом, величина ^набл при достаточно большом к есть просто средняя энергия, "закачиваемая" в бесконечно малую дугу М(6)М(е+б'). Этим определением интенсивности сфокусированного излучения и будем пользоваться в дальнейшем.

Задача фокусировки в линию

Теперь можно перейти к математической формулировке обратной задачи фокусировки излучения в линию X . Пусть р(0) - произвольная кусочнонепрерывная функция 0 < 0 < 1<>. В рамках фазовых оптических элементов требуется найти функцию ф(Е, п) , такую, что отображение I

I : (Х = 5 + f(pE          (Е, П)€ G

Ф L у = п + f Ф^

переводит область G в кривую<£ ,

Кроме того,Pj (0) = р(0), то Ф ности сфокусированного излучения

то есть I G =d£ .

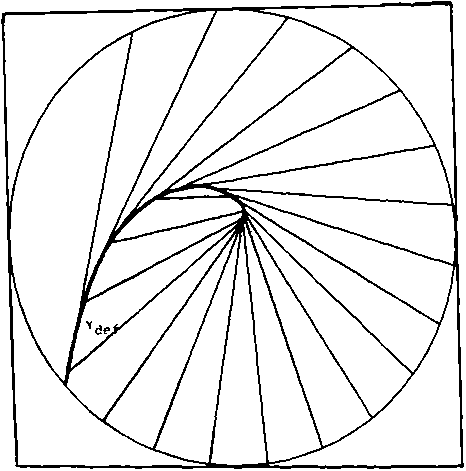
Ф есть задается распределение интенсив- р(0). Возникает вопрос о существовании гладких решений задачи фокусировки в линию. Оказывается, что глядкир решения существуют не всегда. Можно утверждать необходимое и достаточное условие (условие на кривизну кривой [5] и функции р(0)), гарантирующее возможность существования гладкого решения <р. Если говорить о единственности гладкого решения, то их существует не более двух.

Ослабим условия на гладкую функцию ср в G. Пусть срб С2 везде в G, за исключением некоторой гладкой кривой Y^ f« Справедлива теорема [б].

Теорема 4. Пусть of - кусочно-гладкая кривая, а р(0) - произвольная кусочно-непрерывная функция. Тогда поставленная задача синтеза разрешима, то есть существует функция Ф6 С2(G/yde^), такая, что I G = ^ , а Р (0) = р(0).

Алгоритмы решения задачи Фокусировки в линию

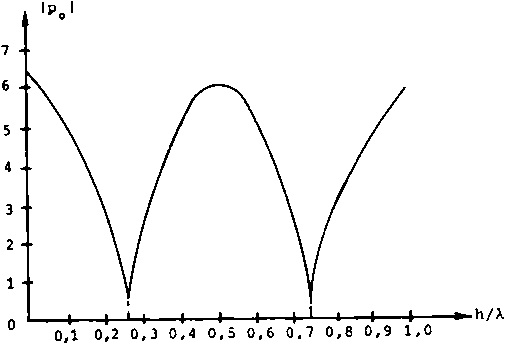
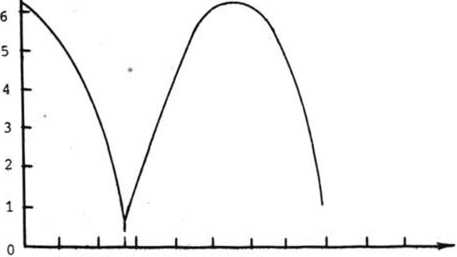
Основываясь на вышеприведенных результатах, можно разработать алгоритмы решения задачи синтеза оптических элементов для фокусировки излучения в линию. Сначала необходимо проверить достаточное условие существования гладких решений [5]. Если такие решения существуют, строится стационарное семейство (г(0)} [1]. В противном случае находится кривая Ydef и стационарное семейство строится в области G\Ydef [б]. Когда стационарное семейство найдено, это означает, что найдено отображение I в области G. Задача восстановления функции ф из соотношений f х = Е + f

Расчет плоских оптических элементов на основе дифракционных решеток (делители пучка, ответвители и т.п.)

Задача создания таких оптических систем, как ответвители, делители пучка, является одной из важных задач современной оптики лазеров. Поскольку расчет дифракционных решеток можно проводить в хорошем приближении как расчет двумерных конструкций, здесь можно применять более сложные модели, основанные на уравнениях Максвелла.

В подобных приближениях можно учитывать влияние поляризации падающего излучения, краевые эффекты, эффекты, связанные с ограниченной проводимостью, и т.п. Аккуратная математическая постановка задачи требует достаточно большого объема. Поэтому ограничимся лишь сравнительными характеристиками результатов, полученных в приближении Френеля и в

Рис. 3. Стационарное семейство {’Г(О)} для случая, когда существует гладкое решение задачи фокусировки

Рис. 4. Стационарное семейство (г(0)} для случая, когда гладкого решения нет; функция ф(Е, д) терпит разрыв на кривой Y^_ef

Рис. 5. Маски оптических элементов (плотность почернения пропорциональна высоте рельефа фазового оптического элемента) для фокусировки в линию с равномерным распределением интенсивности сфокусированного излучения. Гладкое решение существует

Рис. 6. Маски оптического элемента для фокусировки в линию. Гладкого решения нет

рамках модели, использующих приближение Максвелла. Результаты показывают, что если в период решетки укладывается достаточно большое число длин волн, то приближения дают очень близкие результаты. Если период решетки d сопоставим с длиной волны, то модели, основанные на приближении Френеля, уже не являются состоятельными. Для иллюстрации на рис. 7 приведем графики амплитуды отражения р₀ при 6=0 (нормально к решетке) как функции от h-глубины решетки (X - фиксировано). Видно, что при d/X = 9,6 наименьшее отражение в нулевой порядок будет при h/X = 0,25.

a iPo1

h/A

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

Рис. 7. Амплитуда отраженной волны при 9=0 (нормально к плоскости решетки) как функция от h/X:

• а) ^ = 9,6; б) £ = 2,6

При d/X = 2,6 происходит смещение минимума (которого нет в приближении Френеля), и минимальное отражение будет при h/X = 0,28.