Математические модели задачи об упаковке единичных квадратов

Введение. В задачах упаковки целью является размещение некоторого числа меньших объектов без пересечения внутрь большего объекта — контейнера, оптимизируя при этом некоторую целевую функцию. Задачи упаковки в такой формулировке чрезвычайно общи, поэтому существует богатое разнообразие объектов и контейнеров, для которых возможны различные формулировки [1, 2, 3]. Одно большое разделение задач упаковки заключается в том, являются ли размещаемые объекты одинаковыми или нет. В случае упаковки одинаковых объектов одним из простейших является нетривиальный вариант, который будем называть упаковкой 2 х 2 квадратов. Как много 2 х 2 квадратов, ориентированных своими сторонами параллельно осям координат, можно разместить внутри многоугольника Men сторонами, параллельными осям координат и целочисленными вершинами, так чтобы каждый 2 х 2 квадрат занимал ровно 4 единичных квадрата внутри многоугольника M, т. е. имел также целочисленные вершины? Основной объект исследования в данной статье — открытая проблема 56 в списке открытых проблем The Open Problems Project Packing Unit Squares in a Simple

Polygon (Упаковка единичных квадратов в простом многоугольнике). Многоугольник будем называть целочисленным, если все его вершины имеют целочисленные координаты, а стороны параллельны осям координат. Как правило, целочисленный многоугольник не будет выпуклым. Известно, что задача об упаковке квадратов 2 х 2 в целочисленном многоугольнике M является NP-полной [4, 5]. Поэтому интерес для исследователей представляет задача об упаковке квадратов 2 х 2 в целочисленном простом многоугольнике M. Является ли эта. проблема. NP-полной пли она. принадлежит классу задач P (классу задач, решаемых за полиномиальное время), до сегодняшнего дня является открытой проблемой. Для некоторого класса, задач известен полиномиальный алгоритм [6].

Нам понадобятся некоторые операции над множествами.

Определение. Суммой Минковского (алгебраической суммой) двух множеств T 1 ,T 2 на плоскости R² называется множество, обозначаемое T 1 ф T 2 и определяемое по формуле:

T1 Ф T2 = {z G R2|z = x + y, x G T i ,y G T2}.

Определение. Разностью Минковского (алгебраической разностью) двух множеств T 1 ,T 2 на плоскости R² называется множество, обозначаемое T 1 © T 2 и определяемое по формуле:

T1 © T 2 = { z G R2T + z С Ti}.

Одно из соотношений, связывающих эти две операции, таково:

T1 © T2 ф T2 С T1.

Транслят любого множества S на вектор t будем об означать S + 1.

Будем обозначать единичный квадрат, т. е. квадрат со стороной 1 через K1:

K 1 = {x = (x1,x₂) G R2|0 6 x1,x₂ 6 1}.

При этом любой транслят единичного квадрата, также будем называть единичным квадратом.

Основной метрикой будет метрика L^, порождаемая нормой

||(xi,x2)||^ = max(|xi|, |x2|).

Расстояние между единичными квадратами будет определяться расстоянием между их левыми нижними вершинами.

1. Основные результаты. Докажем, что задача об упаковке квадратов 2 х 2 в целочисленном многоугольнике M эквивалентна задаче о размещении в многоугольнике M © K 1 единичных квадратов, так чтобы расстояние между любыми двумя единичными квадратами в метрике L ^ было больше или равно 2. Сформулируем это предложение в виде леммы.

Лемма 1. Задача об оптимальной упаковке квадратов 2 х 2 в многоугольнике M эквивалентна задаче об оптимальном размещении в многоугольнике M © K 1 единичных квадратов, так чтобы расстояние между любыми двумя единичными квадратами в метрике L ^ было больше или равно 2.

Доказательство. Для доказательства каждой укладке 2 х 2 квадратов сопоставим размещение единичных квадратов по правилу: в каждом 2 х 2 квадрате выберем левый нижний единичный квадрат. Легко видеть, что многоугольник M © K 1 с точностью до параллельного переноса совпадает с множеством левых нижних единичных квадратов у 2 х 2 квадратов, которые размещаются внутри многоугольника M. Таким образом, каждой укладке 2 х 2 квадратов в многольнике M соответствует размещение единичных квадратов с расстоянием L ^ >  2. Обратно. Пусть дано размещение в некотором многоугольнике M 0 единичных квадратов с расстоянием L ^ >  2. Сопоставим этому размещению укладку 2 х 2 квадратов по правилу: каждому единичному квадрату размещения сопоставим 2 х 2 квадрат, так чтобы единичный квадрат был левым иижиим у этого 2 х 2 квадрата.. Легко сообразить, что так полученные 2 х 2 квадраты не пересекаются. При этом они все находятся внутри многоугольника M 0 ф K 1. Поскольку мы выбираем M 0 = M © K 1, то лемма доказана, поскольку M © M © K 1 ф K 1.

Рассмотрим двойственную задачу: покрыть как можно меньшим числом 2х2 квадратов многоугольник M 0 = M © K 1. Обозначим это число N. Значение же задачи об оптимальной упаковке 2 х 2 квадратов в многоугольник M обозначим N Справедлива лемма.

Лемма 2. Значения прямой задачи об оптимальной упаковке квадратов 2 х 2 в многоугольник M II двойственной задачи об оптимальцом покрытии квадратами 2 х 2 многоугольника M 0 = M © K 1 удовлетворяют неравенству

N > N .

Доказательство. Пусть дано покрытие квадратами 2 х 2 многоугольника M 0 = M © K 1. Легко видеть, что внутри 2 х 2 квадрата нельзя разместить более одного единичного квадрата в силу леммы 1. И в силу же леммы 1 в многоугольнике M 0 = M © K 1 нельзя разместить более N единичных квадратов, отстоящими друг от друга на расстоянии больше или равным 2. Лемма, доказана.

Эта лемма полезна для ситуации, когда N = N. В этом случае любое оптимальное покрытие квадратами 2 х 2 многоугольника M 0 = M © K 1 будет доказательством оптимальности соответствующего размещения в этом многоугольнике единичных квадратов и в силу леммы 1 доказательством оптимальности укладки в многоугольнике M 2 х 2 квадратов.

Рассмотрим в качестве примера задачу Штейнгауза из [7]. В круг радиуса. 5 упаковать как можно больше единичных квадратов. Мы аппроксимируем эту задачу задачей упаковки 2 х 2 квадратов в многоугольнике на рис. 1.

Достаточно просто накрыть многоугольник M © K 1 67 квадратами 2 х 2. Один из способов показан на рис. 2.

Поскольку многоугольника M © K 1 покрыт 67 квадратами 2 х 2, то в многоугольнике M © K 1 можно разместить не более 67 единичных квадратов. На самом деле в многоугольнике M © K 1 можно разместить 67 единичных квадратов.

Этому размещению соответствует оптимальная упаковка 67 квадратов 2 х 2 в исходном многоугольнике M, которая представлена на следующем рис. 3.

В процессе построения мы с помощью покрытия на рисунке получили доказательство, что данная укладка, является оптимальной. В [7] такого доказательства, не было.

Другие оценки можно получить путем раскрашивания единичных квадратов многоугольника M в 4 цвета, так чтобы любой 2 х 2 квадрат содержал единичные квадраты

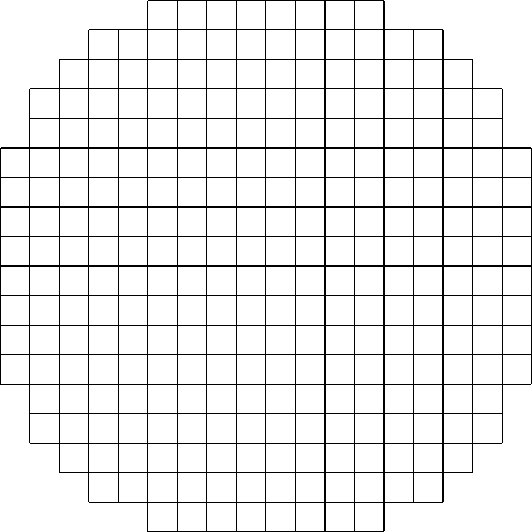
Рис. 1. Многоугольник М всех 4-х цветов. Поскольку любой квадрат упаковки содержит по одной клетке каждого цвета, то справедлива следующая лемма.

Лемма 3. Для оптимального значения задачи об упаковке в многоугольнике M 2 х 2 квадратов справедлива верхняя оценка

N 6 min(N1,N2,N3,N4), где Ni обозначает ттело клеток i-ro тщета в многоугольнике M.

Раскрасок в 4 цвета, таких что любой 2 х 2 квадрат содержит клетки всех четырех цветов, существует не так много, но подобная раскраска все-таки не одна, и поэтому возникает вспомогательная задача подбора такой раскраски, которая позволяет уменьшить оценку леммы 3. Однако эту задачу в данной статье мы рассматривать не будем. Возьмем в качестве основной раскраски раскраску, при которой у клетки с координатами (i,j ) цвет c(i, j) определяется по формуле

c(i,j ) = 1 + i mod 2 + j mod 2.

Выделим в многоугольнике клетки, раскрашенные в цвета 1, 3 (или 2, 4). Тогда любой квадрат 2 х 2 одной из своих диагоналей будет иметь пару клеток, раскрашенных в эти два цвета.

Построим граф задачи об оптимальной укладке в многоугольнике M 2 х 2 квадратов. Вершинами графа будут клетки, раскрашенные в цвета 1, 3. Для лучшей оценки числа укладываемых 2 х 2 квадратов можно выбрать 2 цвета так, чтобы в них присутствовал цвет, дающий значение минимума в лемме 3. Ребра нашего графа будут соединять те

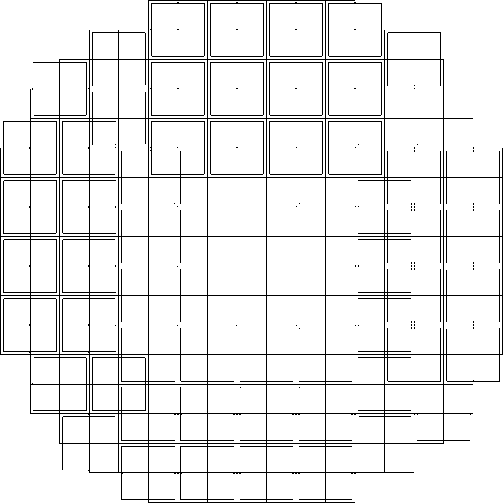
Рис. 2. Покрытие многоугольника M 0 K 1

вершины, которые могут быть накрыты 2x2 квадратом, лежащим внутри многоугольника M.

Легко видеть, что если 2 x 2 квадраты, находящиеся внутри многоугольника M, не пересекаются, то не пересекаются и соответствующие им ребра построенного нами графа. Если бы это соответствие было таково, что непересекающиеся ребра соответствовали бы непересекающимся квадратам, то сразу же можно было бы рассчитывать на существование полиномиального алгоритма для исходной задачи об оптимальной упаковке в многоугольнике M 2 x 2 квадратов. Дело в том, что задача о максимальном числе непересекаю-щихся ребер в двудольном графе является известной задачей теории графов, существует обширная литература по этой задаче и разработано много полиномиальных алгоритмов ее решения.

Таким образом, наша задача эквивалентна задаче о максимальном числе непересека-ющихся ребер в двудольном графе, причем ребра, принадлежащие одному квадрату, не могут быть в одном паросочетании. Геометрически это означает, что каждое ребро заметает две клетки, стороной которых оно является. Это позволяет уточнить оценку леммы 3.

Рассмотрим пример. Пусть в многоугольнике, изображенном на рис. 4, необходимо упаковать как можно большее число 2 x 2 квадратов. Раскрасим этот многоугольник как на рис. 5.

Из этого рисунка видно, что больше 7 квадратов 2 x 2 упаковать в многоугольник M невозможно, поскольку внутри прямоугольника M только 7 клеток цвета 3. По двум цветам 1, 3 построим граф задачи об оптимальной укладке в многоугольнике M 2 x 2 квадратов. После поворота на 45 градусов он будет выглядеть как на рис. 6:

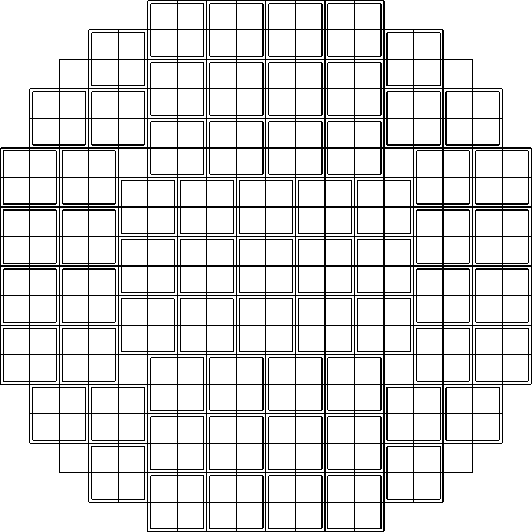
Рис. 3. Оптимальная укладка в многоугольнике М квадратов 2 х 2

Рис. 4. Многоугольник M ⁰

Разделим ребра на внутренние и граничные. Граничные ребра заметают один квадрат, внутренние ребра заметают два квадрата. Отсюда следует, что внутреннее ребро в паросо-четании может быть только одно, если у нас в паросочетании 7 ребер. То есть граничных ребер в искомом паросочетании должно быть ровно 6. Но в нашем графе 12 граничных ребер, образующих простой цикл. Поэтому граничные ребра в паросочетании могут быть либо как на рис. 7, либо как на рис. 8.

В обоих случаях они заметают все квадраты одного цвета, если их раскрасить в два цвета в шахматном порядке. Поэтому поскольку внутреннее ребра заметает два квадрата разного цвета, то внутреннего ребра для обоих паросочетаний не найдется. Поэтому

2 1

2 1 7 Т 7 т

3 2 3 2 3 2

4 1

3 Т к т 3 т

7 Т

Т

7 Т

т 3 т к т 3 т

т

7 т

т

7 Т

т 3 т к т 3

7 Т

Т

4 1

Рис. 5. Раскраска, многоугольника. М’

Рис. 6. Граф задачи об оптимальной укладке

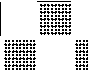
Рис. 7. Первое паросочетаиие

Рис. 8. Второе паросочетаиие

максимальное паросочетаиие для нашей задачи содержит не более 6 ребер. То есть в многоугольник на рис. 4 помещается не более 6 квадратов 2 х 2.

Сформулируем задачу об оптимальной упаковке квадратов 2 х 2 в виде задачи целочисленного линейного программирования. Каждому положению квадрата 2 х 2 поставим в соответствие целочисленную переменную xi,j, где i, j — координаты левой нижней вершины. Тогда каждая клетка i, j должна принадлежать только одному квадрату, что соответствует ограничению xi,j + xi-1,j + xi,j-1 + xi-1,j-1 6 1'

Поскольку левая нижняя клетка i,j квадрата 2 х 2 соответствует клетке из M © К₁, то задача целочисленного линейного программирования будет формулироваться следующим образом:

Е

x i,j ^ max

(m)gm eKi при ограничениях xi,j + xi-1,j + xi,j—1 + xi- 1,j-1 6 1,

X i,j G {0,1}.

В этих ограничениях мы не следим, чтобы все 4 квадрата 2 х 2 в ограничениях были внутри многоугольника M, поскольку квадраты 2 х 2 вне много угольника M могут только усилить ограничения, но никак не повлиять на целевую функцию, и потому, приняв их значения равными нулю, мы получим задачу с тем же оптимальным значением. Но с точки зрения канонического представления задачи об оптимальной упаковке важно в неравенствах выписывать только те переменные, которым соответствуют квадраты 2 х 2, лежащие внутри многоугольника M. Тогда появляется возможность ввести понятие доминирования одной клетки многоугольника M над другой.

Определение. Скажем, что единичная клетка (квадрат)C₁ G M целочисленного многоугольника M доминирует над клеткой C₂ G M (обозначение C₁ V С₂), если множество

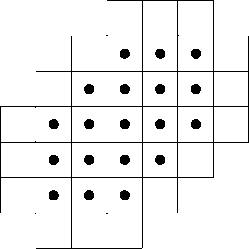
Рис. 9. Многоугольник М’ содержащих ее квадратов 2 х 2, лежащих внутри M, содержит в себе множество квадратов 2 х 2. лежаттщх внутри M и содержащих клетку C2.

Это определение связано с тем, что если С ₁ >- C2, то неравенство, соответствующее клетке C2, следует из неравенства, соответствующего клетке С₁, и таким образом становится избыточным. В этой связи в многоугольнике M можно выделить доминирующие клетки и соответствующие им неравенства, тем самым уменьшить размер задачи целочисленного линейного программирования для задачи об оптимальной упаковки.

В качестве примера выпишем задачу целочисленного линейного программирования для задачи об оптимальной упаковке в многоугольнике, показанном на рис. 6, квадратов 2 х 2. На следующем рис. 9 показаны доминирующие клетки.

Задача целочисленного линейного программирования будет выглядеть следующим образом:

max{xi,2 + xi,3 + X2,1 + x2,2 + x2,3 + x2,4 + x3,i + x3,2 + x3,3 + x3,4 + x3,5 + x4,2 + x4,3 + x4,4 + x4,5 + x4,6 + x5,3 + x5,4 + x5,5 + x5,6 + x6,4 + x6,5} при ограничениях x1,1 + x1,2 + x2,1 + x2,2 6 1; x1,2 + x1,3 + x2,2 + x2,3 6 1; x1,3 + x1,4 + x2,3 + x2,4 6 1;

^x 2 , 1 + x 2 , 2 + ^x 3 , 1 + ^x 3 , 2 6 1; x 2 , 2 + ^x 2 , 3 + ^x 3 , 2 + ^x 3 , 3 6 15

^x 2 , 3 + ^x 2 , 4 + ^x 3 , 3 + ^x 3 , 4 6 1; ^x 2 , 4 + ^x 2 , 5 + ^x 3 , 4 + ^x 3 , 5 6 1;

^x 3 , 1 + ^x 3 , 2 + ^x 4 , 1 + ^x 4 , 2 6 1; ^x 3 , 2 + ^x 3 , 3 + ^x 4 , 2 + ^x 4 , 3 6 1;

^x 3 , 3 + ^x 3 , 4 + ^x 4 , 3 + ^x 4 , 4 6 1; ^x 3 , 4 + ^x 3 , 5 + ^x 4 , 4 + ^x 4 , 5 6 1; ^x 3 , 5 + ^x 3 , 6 + ^x 4 , 5 + ^x 4 , 6 6 1;

^x 4 , 2 + ^x 4 , 3 + ^x 5 , 2 + ^x 5 , 3 6 1; ^x 4 , 3 + ^x 4 , 4 + ^x 5 , 3 + ^x 5 , 4 6 1;

x 4 , 4 + x 4 , 5 + ^x 5 , 4 + ^x 5 , 5 6 1;   x 4 , 5 + x 4 , 6 + x 5 , 5 + x 5 , 6 6 1;

• x5,3 + x5,4 + x6,3 + x6,4 61;

• x5,4 + x5,5 + x6,4 + x6,5 61;

• x5,5 + x5,6 + x6,5 + x6,6 6

x i,j e {0,1}.

Решение этой задачи с помощью свободно распространяемой программы LPSolve дает решение 6.

Заключение. В статье приведены результаты разработки и исследования моделей, методов и алгоритмов для решения задачи 56 в списке открытых проблем вычислительной геометрии The Open Problems Project Packing Unit Squares in a Simple Polygon.