Математические основы биткойн-блокчейна

Сегодня биткойн продолжает набирать популярность, а индустрия разрабатывать все новые приложения для работы с криптовалютой. Одной из причин такой популярности является строгая математическая база, на которой строится биткойн. Благодаря этому система функционирует в условиях полного отсутствия доверия между участниками сети, исключая воздействие человеческого фактора. Поэтому хотелось поговорить о математических основах биткойн-блокчейна — эллиптических кривых, ECDSA и ключах [1].

Алгоритм цифровой подписи эллиптической кривой

В протоколе биткойна зафиксирован набор параметров для эллиптической кривой и её конечного поля, чтобы каждый пользователь использовал строго определенный набор уравнений. Среди зафиксированных параметров выделяют уравнение кривой (equation), значение модуля поля (prime modulo), базовую точку на кривой (base point) и порядок базовой точки (order). Этот параметр подбирается специально и является очень большим простым числом.

Эллиптическая кривая Blockchain - это, в основном, общедоступная книга, в которой участники вводят данные и подтверждают их принятие транзакции с помощью алгоритма цифровой подписи эллиптической кривой (ECDSA). Эллиптическая кривая - это уравнение вида y2 = x3 + a x + b. В биткойне и большинстве других реализаций a = 0 и b = 7, так что это просто y2 = x3 + 7 (рис. 1). Эллиптические кривые имеют несколько интересных свойств, например, невертикальная линия, пересекающая две некасательные точки на кривой, пересечет третью точку на кривой. Суммой двух точек на кривой P + Q называется точка R, которая является отражением точки -R (построенной путем продолжения прямой (P; Q) до пересечения с кривой) относительно оси X. Действительно, на кривой можно определить «сложение», считая третью точку, соответствующую двум заданным. Это в основном то, что делается в ECDSA, за исключением того, что операции выполняются по модулю некоторого большого простого числа M.

Вычисление открытого ключа выполняется с помощью тех же операций удвоения и сложения точек. Это тривиальная задача, которую обычный персональный компьютер или смартфон решает за миллисекунды. А вот обратная задача (получение секретного ключа по публичному) — является проблемой дискретного логарифмирования, которая считается вычислительно сложной. Лучшие известные алгоритмы ее решения, вроде ро Полларда, имеют экспоненциальную сложность. Для secp256k1, чтобы решить задачу, нужно порядка 2128операций, что потребует времени вычисления на обычном компьютере, сопоставимого со временем существования Вселенной.

Следует подчеркнуть, что наш пример включает в себя чрезвычайно скромные целые числа. В реальном приложении Bitcoin или blockchain эти целые числа обычно составляют 256 бит в длину, что значительно увеличивает стоимость выполнения вышеуказанных операций, но, с другой стороны, очень значительно увеличивает затраты, требуемые для того, чтобы кто-то «нарушил» систему, например путем вычислительной попытки восстановить закрытый ключ из открытого ключа [2].

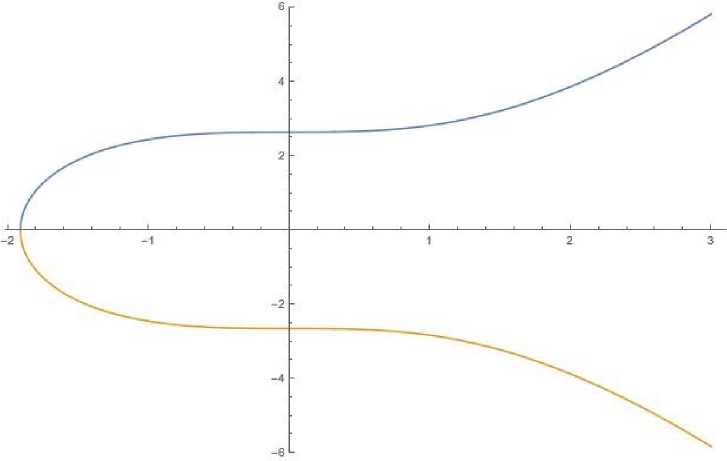
Рис.1. Уравнение y2 = x3 + 7.

Таким образом, математика и необходимые вычисления для реализации этой схемы, конечно, не являются тривиальными. Тем не менее, у нас есть эффективная односторонняя функция: относительно легко проверить подпись, но очень сложно работать с общедоступными данными, такими как открытый ключ, для получения критического закрытого ключа.

Безопасность ECDSA связана со сложностью задачи поиска секретного ключа, описанной выше. Помимо этого, безопасность исходной схемы зависит от «случайности» выбора k при создании подписи. Если одно и то же значение k использовать более одного раза, то из подписей можно извлечь секретный ключ. Поэтому современные реализации ECDSA, в том числе используемые в большинстве биткойн-кошельков, генерируют k детерминировано на основе секретного ключа и подписываемого сообщения.

ECDSA - это суть того, как работают bitcoin и другие приложения blockchain. Эта схема сопротивлялась некоторому довольно обширному тестированию слабых мест, как математически, так и вычислительно. Несколько неудач, которые произошли на практике, как правило, заключались в том, что пользователи не проявляли осторожности в защите своих закрытых ключей, иначе они использовали довольно стандартный генератор псевдослучайных чисел для создания секретных ключей, которые затем использовали злоумышленники.

Как и во всех тех технологиях, которые мы используем в нашей цифровой эпохе, самыми слабыми местами являются пользователи, которые не проявляют достаточной бдительности.