Математические основы построения функции плотности вероятности в задачах обнаружения
Автор: Макошенко Д.М., Петрова Е.В.
Журнал: Форум молодых ученых @forum-nauka
Статья в выпуске: 7 (23), 2018 года.
Бесплатный доступ
В статье рассматривается один из способов решения проблемы сингулярности КПМ возникающей в случае однопозиционной локации при измерении ПВР на двух поляризациях. Так же рассматриваются особенности построение функции плотности вероятности.
Пвр, кпм, вектор, линейное многообразие, обнаружение объекта
Короткий адрес: https://sciup.org/140283905
IDR: 140283905
Текст научной статьи Математические основы построения функции плотности вероятности в задачах обнаружения
В статье рассматривается случай однопозиционной локации ковариационно - поляризационной матрицы (КПМ) выборок поляризационного вектора рассеивания объектов (ПВР). При этом единичный отсчет ПВР может быть представлен в виде комплексного вектора [1,2]
^(О и(^)лп + <*0^(02? + и(^)ш ,ос0
О ирыН0, 1 npuHv
где: ^ 1 1 л.: - ПВР подстилающей поверхности в момент времени ; ^
ПВР объекта; ^ ' ' - - шум приемных каналов.
Поскольку элементы ПВР -;. = -.; в силу однопозиционной локации, то ранг КПМ равен трем, но на практике из-за шумов КПМ является плохо обусловленные с рангом равным 4. Сингулярность КПМ приводит к некоторым особенностям определения плотностей вероятностей статистических моделей сигналов [1].
Сингулярность КПМ ПВР приводит к локализации значений ПВР L" в ■ - плоскости 1 ', размерность которой - ~ = " < n , где n = 4. Поэтому, вероятность локализации ПВР К в плоскость, не пересекающую -' ^ ', будет равна нулю, т.е. ПВР I" в С4 имеет нулевую плотность распределения [3,4].
Для решения этой проблемы выберем в направляющем подпространстве -' I 1 линейного многообразия -' ^ 1, какой - либо направляющий орт , образованный из направляющего орта , исходного пространства < при помощи линейного преобразования с матрицей В размера ' ;\ [3]. Если У - произвольный вектор подпространства -' 1 1 в базе ^l поэтому координаты любой точки I" ^ -■ I ■ можно выразить как I" = В У , а любую точку I" е -' 1 можно представить в виде [5,6]
I" = By + I • ^ : е -' ^ 1.
Если случайный n - мерный вектор, : е , то е -' ^'.
Переведем этот случайный вектор в базис с направляющими ортами ^l и обозначим такой "- мерный вектор через У . Тогда из (2) получим
V =в 7 (L"-L":)
Случайный вектор У является " - мерным в " - мерном подпространстве, не локализуется ни в каком подпространстве меньшей размерности и его ковариационная матрица Т будет невырожденной. Тогда для У будет существовать плотность вероятности [4,6]
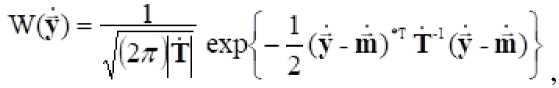
где I I - определитель матрицы; in - математическое ожидание 5 .
Переведем (4) в исходный базис ec , т.е. перейдем к переменной L. Для чего выберем в качестве т - мерного базиса E(U) все т нормированных собственных векторов ^0 = 1, r) , соответствующих ненулевым собственным значениям A КПМ M (rgM=r) . Тогда матрица перехода В размера ПХГ будет состоять из векторов , расположенных столбцами [5].
Матрица В должна удовлетворять условию в"7 6 =I, где I - единичная матрица r x г . Если iri = < >, то
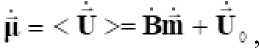
где < > - знак статистического усреднения.
Поляризационно - ковариационная матрица равна:
м = 4 < (и - дхи ■ pr >
^ B I B . (6)
Из (5) находим
T = B 7 MB
Проведя в (4) преобразования с учетом (2),(6),(7), получим выражение для плотности вероятности случайного ПВР I в исходном базисе [7]
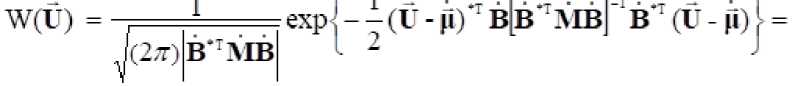
, 1 . exp! -1 (U - p) ’’ M" (U - jf) 1
J(2^)B'TMB I 2
где M= - обобщенная обратная матрица Мура [6].
Таким образом, можно дать следующее определение для многомерного нормального распределения, включающего и вырожденный случай: n – мерный случайный вектор I с математическим ожиданием pи ковариационной матрицей м распределен нормально, если существуют преобразования (6), (7).
На практике сингулярные КПМ ПВР объектов встречаются редко. Ковариационные матрицы м , как правило, вычисляются по экспериментальным данным. Погрешности измерений приводят к тому, что оценки матрицы м получаются не сингулярные, но плохо обусловленные. При этом задача определения обратной матрицы м1 будет некорректной, так как ее решение неустойчиво, ибо малые изменения входных данных могут вызвать какие угодно большие (по норме) изменения решений. Устойчивость решения связана с набором собственных чисел л матрицы м и падает с ростом отношения “^ивс ^мин .
Выходом из данного положения может стать предположение о том, что данная плохо обусловленная оценка матрицы м - результат погрешностей измерения истинно сингулярной матрицы м . По очереди находим " h ■ наибольшие I и соответствующие им матрицы м и вычисляем значения
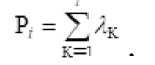
при этом величина
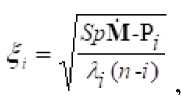
где 5>М - след матрицы м , может служить оценкой качества исчерпывания пространства, занимаемого t собственными векторами. Выбираем граничное значение для , при достижении которого процедуру го останавливаем. Полученные г нормированных собственных векторов иг составляют базис τ - плоскости L(M) . Из этих векторов составляем матрицу преобразования В размера пх г . Проекция совокупности L' вг - плоскость LA будет иметь выраженную ковариационную матрицу М , сингулярный скелет матрицы м . Дальнейшая методика получения закона распределения случайного вектора t такая же, как и в случае сингулярных матриц.
При измерении ПВР ошибки приводят к тому, что КПМ получается плохо обусловленной, т.е. detM^O, но величина его очень мала. В этом случае задача обнаружения становится некорректно поставленной, так как для сингулярных матриц допускается бесконечное множество решений, а для плохо обусловленных матриц решение неустойчиво (малые изменения входных данных могут вызвать какие угодно большие изменения решения)
[6]. То есть, все значения случайного вектора LI локализуются в r – подпространстве Ци) , размерность которого diin L(U) = rgM = /■ < n . Следовательно, необходимо выбрать базис размерности r , пересчитав в который IиM линейно, можно корректно записать решающее правило.
Таким образом, в соответствии с [8] необходимо построить сингулярный скелет для матриц
M = MT + M
где M1,M; - КПМ полученные по выборкам ПВР элемента разрешения( pd X ^pb ) и окрестности элемента разрешения ( Nod x Noi> ) рис. 1
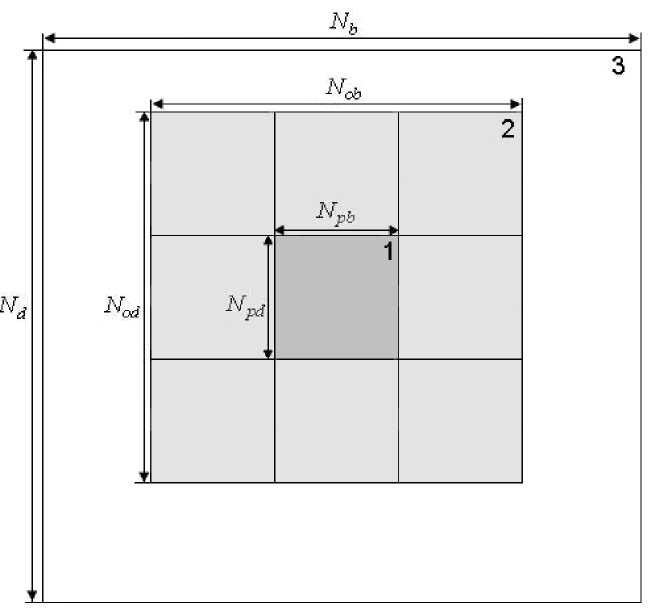
Рис. 1. Принцип формирования окон усреднения.
^х^д - общее количество пикселей исследуемого радиоизображения (белая область), Nod x Nob - количество пикселей фрагмента радиоизображения, используемого для оценивания характеристик фонового отражения (светло-серая область), ^pd X ^pb - количество пикселей фрагмента радиоизображения, подвергаемого анализу на предмет обнаружения объекта (темно-серая область).
Определив все собственные значения s и нормированные собственные векторы и отбросив (4-r) вектора, соответствующих равным нулю ^ , строим унитарную матрицу ® ^:L.;. Тогда координаты любой точки I в направляющем пространстве Е (U) линейного многообразия L(U) могут быть выражены в виде U = BL , где L - случайный вектор r -мерный в r - мерном пространстве.
Ковариационная матрица MH вектора L будет также r - мерной и невырожденной.
В связи с тем, что на построение цифрового изображения влияет большое количество случайных независимых факторов функцию плотности вероятности ПВР можно предположить гауссовой. Это справедливо если длина волны меньше размеров обнаруживаемых объектов, например, для измерителей работающих систем, работающих в сантиметровом и дециметровом диапазоне волн, а в качестве обнаруживаемых объектов выступают автомобили, строения и т.д.
Свойство нормальности ПВР сильно упрощает вид решающей функции, так как решающая функция оказывается линейной комбинацией наблюдений, и ее распределение вновь будет нормальным.
Поэтому, закон распределения ПВР если верна одна из гипотез: "": (наличие только земной поверхности) или "" (наличие земной поверхности и объекта) можно записать в виде [5, 7]
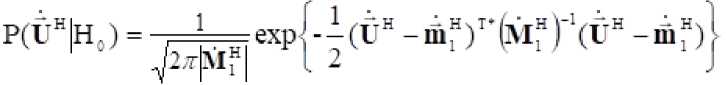
, (12)
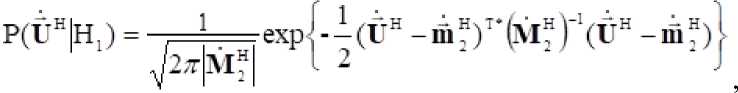
1 \гн \тн <гн н
- определители матриц ; - вектора МО для выборок земной поверхности и разрешающего объема соответственно.
* * • _■_гт * т ^_1_ * _"_у "т^_1_
ин - RT U М? В МВ м в МВ , ,
Условный логарифм отношения правдоподобия будет иметь вид [5]:
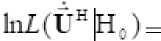
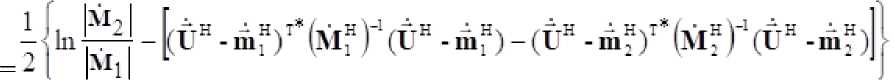
Аналогичным образом находится
Рассматриваемая методика корректна в случае, когда ранги КПМ элемента разрешения и окрестности элемента разрешения равны. В противном же случае, пространства, в которых находятся области локализации признаков, несоизмеримы [6].
В случае двух-альтернативного решения, значение условных вероятностей ошибок первого a и второго рода могут быть оценены путем определения условных законов распределения логарифмов отношений правдоподобия и их интегрирования в определенных приделах. При большом n распределение логарифмов отношения правдоподобия lnL приближается к нормальному, и имеют место асимптотические соотношения
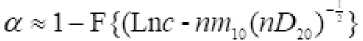
P ^\ - F{(Lnc - nn^ (nDny-} (16)
где:
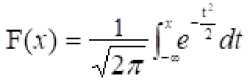
интеграл Лапласа; "'io = »ii{ln£(U)|H,}
»>„ = »., {In Z.(U)|HJ
D^ — ^^2 {b^ (U) |Kq }* ; -^^21 — "^^2 ^ ^ ■^'*‘ ^* '*1^1/ математические ожидания и дисперсии логарифмов отношения правдоподобия при справедливости гипотез H:и Hi соответственно; C порог принятия решения.
Величину c можно принять равной единице, если считать нулевыми стоимости правильных решений. Тогда ошибки первого и второго рода [4].
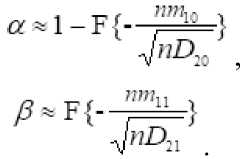
Список литературы Математические основы построения функции плотности вероятности в задачах обнаружения
- Бурданова, Е.В. Особенности построения алгоритмов обработки информации в радиолокационных системах с поляризационным зондированием. [Текст]/ Е.В. Бурданова, И.И. Олейник, А.П. Денисов, Ю.П. Новоченко // Сборник трудов Четвертой международной научно-практической конференции «Исследование, разработка и применение высоких технологий в промышленности», т.
- - Санкт-Петербург. 2007 С. 89-91. 2. Родимов, А. Л. Статистическая теория поляризационно-временной обработки сигналов и помех [Текст]/ А. Л. Родимов, В. В. Поповский -Радио и связь, Москва - 1984.
- Муромцев, В.В. Особенности разработки и реализации алгоритмов обработки и отображения информации в обзорной РЛС с полным поляризационным зондированием [Текст]/ В.В. Муромцев, Е.В. Бурданова, Д.Б. Храбростин, И.И. Олейник// Материалы XXIV Симпозиума «Радиолокационное исследование Природных сред» - Санкт-Петербург. - 2006.-С. 245-250.
- Либенсон, М.Н. Автоматизация распознавания телевизионных изображений [Текст]/ М.Н. Либенсон, А.Я. Хесин, Б.А. Янсон - М.: Энергия, 1975. - C. 160
- Бурданова, Е.В. Использование двух - альтернативных решений в задачах проверки гипотез о наличии радиолокационных объектов на фоне подстилающей поверхности в системах с поляризационной обработкой информации [Текст]/ Е.В. Бурданова // «Научные ведомости БелГУ» Серия информатика, прикладная математика, управление. №7 (38) Вып 4. Белгород 2007 - С. 207-213
- Фукунага, К. Введение в статистическую теорию распознавания образов [Текст]/ К. Фукунага- М.: Наука, 1979. - C. 387
- Бурданова, Е.В. Техническая реализация алгоритмов обнаружения целей на фоне помех в локационных системах с поляризационным зондированием [Текст]/ Е.В. Бурданова, Е.Г. Жиляков, А.П. Денисов И.И. Олейник, А.И. Синани //Вопросы радиоэлектроники Серия «Электронная вычислительная техника» Выпуск 1.- М. 2008 - C. 60-68
- Гусев, Г. К. Поляризационная модуляция [Текст]/ Г.К. Гусев, Ф.Д. Филатов, А.И. Сополев - М.: Сов. Радио, 1974. - С. 288


