Математический анализ различных вариантов наружного чрескостного остеосинтеза

При лечении переломов и деформаций пяточной кости используются методики наружного чрескостного остеосинтеза спицевым аппаратом Г.А. Илизарова [3]. Как дополнение к известным спицевым компоновкам аппарата, нами были разработаны методики спице-стержневой и стержневой фиксации фрагментов костей. Методом математического моделирования была произведена сравнительная оценка жесткости систем, возможных перемещений и деформаций, а также рассчитаны напряжения, возникающие при взаимодействии элементов конструкций с костной тканью.

Цель работы состояла в сравнительном ана-

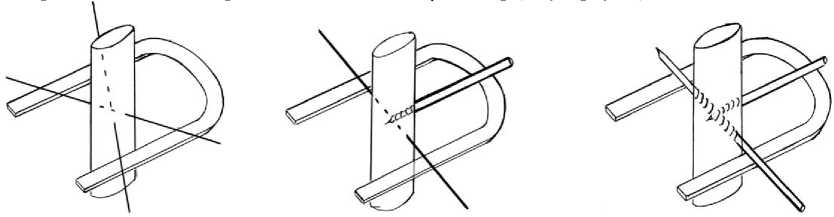
а) д вухспицевая конструкция

б) с пице - стержневая конструкция

в) д вухстержневая конструкция

Рис. 1. Схемы фиксации.

лизе различных способов фиксации костных фрагментов при переломах и деформациях пяточной кости (рассматривались методы наружного чрескостного остеосинтеза).

Рассматриваемые двухспицевая, спицестержневая и двухстержневая конструкции схематически изображены на рис. 1.

Основу этих конструкций составляет полу- кольцевая опора, к которой крепятся спицы и стержни. Спицы снабжены упорной площадкой. Используются стержни двух видов – консольные и сквозные. Стержни имеют две разновидности резьбы: метрическую (для крепления к опоре) и упорную (для соединения с костью).

Оценка напряжений, возникающих при взаимодействии элементов конструкций с костной тканью. Усилия, создаваемые в аппарате для коррекции положения отломков, передаются на кость при помощи упоров на спицах и резьбового соединения в стержнях (рис. 2).

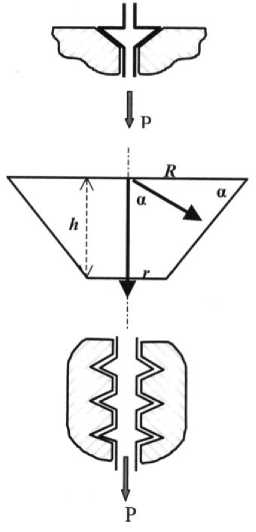
Рис. 2. Схемы упора на спице и резьбового соединения. P - сила натяжения.

Для определения максимально допустимой силы, необходимой для удержания отломка в фиксированном положении, важно оценить напряжения, возникающие при этом в костной ткани.

Площадь поверхности контакта упора на спице с костью может быть вычислена как пло- щадь поверхности усеченного конуса

S = П R + r ) L = П R + r )V h ² + ( R — r )² ■

При натяжении спицы силой P , напряжения, возникающие в костной ткани, приближенно равны (j = ^{P cos a} . Так как tg _a = h , то

S                   R - r

1             R - r      ■ cos a =     — =----------

71 + tg² a   7 h ² + ( R - r )²

Поэтому _o ______ ^{( R} - ^r ) P ______₌ k p ,

n ( R + r )( h ² + ( R - r )²)    ¹

^где k. =

R - r

■

n ( R + r )( h ² + ( R - r )²)

В частности, для применяемых на практике спиц имеем r=0,1 см, R ® 0,4 см, h ® 0,45 см, k » 2

2 см

При использовании стержня, имеющего с костью резьбовое соединение, напряжения, воз- никающие в костной ткани, ниже, чем при использовании спицы с упором. Это достигается за счет большей площади контакта резьбы стержня с костным фрагментом, что создает меньшее напряжение в кости. Если наружный диаметр резьбового соединения равен 2R, а внутренний - 2r, то на каждом витке резьбы площадь соприкосновения стержня с костной тканью можно приближенно вычислить как площадь кольца s1 = nR2-r2). Для принятых на практике значений 2R=0,65 см, 2r=0,45 см 51x0,173 см2. Площадь контактной поверхности s=ns1, где n - количество витков. Поэтому напряжение, возникающее в костной ткани при использовании резьбового соединения, тем меньше, чем больше число витков. В частности, для приведенных параметров спицы и стержня напряжение резьбового соединения будет заведомо меньше напряжения, создаваемого спицей с упором, при наличии не менее трех витков в контактной области для одинаковой силы натяжения. Следует отметить, что число витков не может быть большим, так как при этом уменьшается шаг резьбы и возникает опасность среза резьбы в костном фрагменте.

При оценке перемещений и деформаций в стержневых и спице-стержневых конструкциях использовались схемы расчета прогибов балок, основанные на гипотезе Бернулли [1]. При этом деформации спиц определялись по стандартной методике [2].

Деформации стержневых элементов конструкций оценивались с использованием модельных задач [1].

Рассматривались различные способы нагрузки балки: консольная балка, нагруженная моментом пары сил, приложенных к свободному концу (рис. 3 а); консольная балка, нагруженная моментом сосредоточенной силы, приложенной к свободному концу (рис. 3 б); свободно опертая по краям балка, нагруженная сосредоточенной силой, приложенной в середине (рис. 3 в).

Дифференциальное уравнение упругой линии балки (в данном случае оси симметрии) имеет вид (см., например, [1]):

у Ч х ) = 1- M ( х ), EI

где y ( x ) - величина смещения оси балки в точке с абсциссой x ;

E - модуль Юнга;

I - момент инерции поперечного сечения балки; для балки с круглым поперечным сечением диаметра d [ = ra i⁴/64 ;

M ( x ) - момент, создаваемый приложенной нагрузкой.

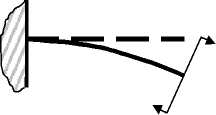
а) Консольная балка, нагруженная моментом пары сил, приложенных к свободному концу.

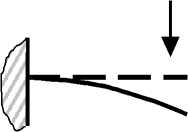
б) Консольная балка, нагруженная сосредоточенной силой, приложенной к свободному концу.

в) Свободно опертая по краям балка, нагруженная сосредоточенной силой, приложенной в середине.

Рис. 3. Модельные задачи.

В случае а) консольная балка нагружена моментом М₀ , создаваемым парой сил. Значение M(x) постоянно во всех сечениях и равно М₀,

начальные условия имеют вид y(0)=0,   у'(0)=0 .

Дважды интегрируя (1), получим выражение для прогиба

, .       1

У ⁽ x ) =     ^M 0 x + ^C 1 x + ^C 2 ’

2 EI где Ci, C2 - постоянные интегрирования. Используя начальные условия (2), находим, что С1=С2=0.

Таким образом, в случае а) решение уравнения (1) с начальными условиями (2) имеет вид z .       1           2

у ⁽ x ) =      M о x .

2 EI

Максимальный прогиб и наибольший угол поворота поперечного сечения достигаются при x = L и вычисляются по формулам

у ( L) = M O LL , у ‘ ( L ) = ML .

2 EI           EI

В случае б) обозначим P сосредоточенную силу, которой нагружена балка. Тогда выражение для момента M(x) в (1) имеет вид

M (x) = P (L - x), а начальные условия – (2). Решение в этом случае задается формулой у (x) =     (3L - x).

6 EI

Так же, как и в предыдущем случае, максимальный прогиб и наибольший угол поворота поперечного сечения достигаются при x = L .

у (L) =----, у'(L) =.

3 EI2

Изгиб шарнирно опертой по краям нагруженной сосредоточенной силой P ,

балки, прило-

женной в центре (рис. 3 в). Обозначим длину балки 2L . Выражение для изгибающего момента

М ( x ) имеет вид

M ( x ) = -

P

- —x при 0 <  x <  L

P

- —(2 L - x ) при L <  x <  2 L

Начальные условия - у (0)=0, y ( 2L )=0.

В силу симметрии задачи ясно, что наибольшие прогибы будут в центре, в точке приложения силы, а угол поворота поперечного сечения в этой же точке отсутствует ( y ( L )=0). Поэтому решение для всей балки мы можем

получить как симметричное продолжение относительно прямой x=L решения задачи на интервале [ 0; L ] для м ( _x ) = - P _x с начальными усло

виями у (0) = 0, y ( L )=0. Решение имеет вид

( x ) = P ( 3 Lx - x з) . Максимальный прогиб ^у 1 )   12 ei\        )

лучаем при x=L

^{PL 3} у ⁽ L ) =

6 EI

по-

Результаты расчетов показывают, что при действии одинаковых сил прогибы двухспицевой конструкции ® в 2-2,5 раза больше, чем прогибы спице-стержневой, которые, в свою

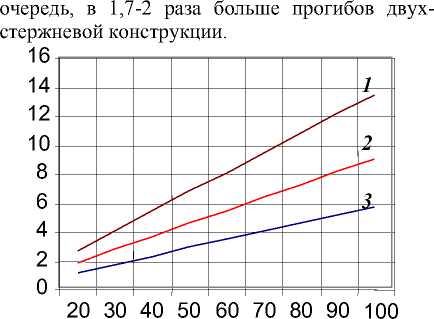
Рис. 4. Максимальные прогибы для консольной балки (рис. 3, б) при различных L: 1 – L= 6см, 2 – L=7см, 3 – L= 8см. По оси абсцисс отложена нагрузка P.

ВЫВОДЫ

Из трех рассмотренных конструкций максимальная жесткость фиксации достигается при использовании стержневых конструкций.

Большая площадь контакта резьбы стержня с костным фрагментом создает меньшее напряжение в кости, уменьшая вероятность ее разру-

шения. При использовании спицевых конструкций существует большая опасность прорезывания костной ткани, что приводит к увеличению зазоров между костью и спицей, снижающих жесткость фиксации.