Математический анализ устойчивости неизотермической вытяжки полого волокна

Сегодня волоконная оптика прочно заняла лидирующие позиции среди различных отраслей науки и техники. Волоконно-оптические технологии широко используются в системах дальней и локальной связи, приборостроении, медицинских датчиках и др.

Одним из главных этапов производства волокна является его вытяжка. При этом процессе цилиндрическая заготовка подается в разогретую печь вертикального типа. В результате кварцевое стекло плавиться, образуя свободную жидкую струю, которая опускается на приемный барабан. Вращение барабана создает натяжение, которое обеспечивает утончение нити [7]. При этом требуется высокая степень устойчивости параметров, чтобы отклонение диаметра готового волокна не превышало 1 %. Однако, как и любой процесс, вытяжка волокна подвержена внешним флуктуациям, в частности колебанию температуры нагревательного элемента, отклонению диаметра заготовки и др., которые, в свою очередь, могут негативно повлиять на характеристики готового волокна. Поэтому очевидна важность анализа линейной устойчивости рассматриваемого процесса и его реакции на возникающие возмущения.

Деревянкина Анна Леонидовна старший преподаватель кафедры прикладной математики. Пермский национальный исследовательский политехнический университет, город Пермь. Сфера научных интересов: устойчивость технологических процессов, вытяжка волокна. Автор более 20 опубликованных научных работ.

Математическая модель неизотермической процесса вытяжки полого волокна Схема вытяжки полого волокна и его характеристики показаны на Рисунке 1.

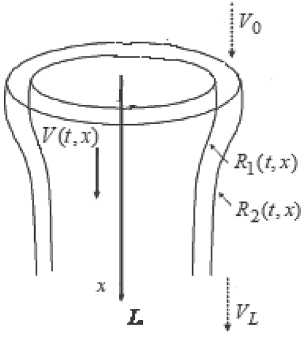
Рисунок 1. Схема вытяжки полого волокна

Рассмотрим одномерную систему координат (здесь пространственная ось ориентирована вниз). Направление аналогично направлению вытяжки (вдоль оси симметрии). Процесс формирования оптического волокна описывается течением одноосной ньютоновской жидкости с переменной вязкостью, зависящей от температуры. Математическая

Математический анализ устойчивости неизотермической вытяжки полого волокна модель такого процесса описывается системой уравнений в частных производных: первое уравнение – уравнение движения, второе и третье – уравнения неразрывности, четвертое – уравнение теплопроводности (одномерная аппроксимация) [2; 8].

2i 21/ xxl dV(z,t)          x8V(z,t)

P( R (z, t) - R '(z, t ))l — ---+ V(z, t)—

2                 v d t                dz

= ^( 3ц( R22( z, t) - R12( z, t)) VzA + y( R2( z, t) + R1( z, t))|, dz dRi2(z, t) + d(V(z, t)Ri2(z, t)) = PoRi2 (z, t)R22 (z, t) - /R 1 (z, t)R2 (z, t)(R1 (z, t) + R2 (z, t))

81                8z                             ^(T)(R2(z,t)2 -Ri(z,t)2),

8 ^R 22 ^{( z} , t ) + 8 ^{(V ( z} , t ) ^R 22 ^{( z} , t)) = P o R i ^{2 ( z} , t ) ^R 22 ^{( z} , t ) ^- Y R 1 ^{( z} , t ) ^R 2 ^{( z} , t ) ^{( R} 1 ^{( z} , t ) + ^R 2 ^{( z} , t))

8 1                 8 z                                 ц ( R 2 ²( z , t ) - R 1 ²( z , t ))

2/ x 2i, xxl 8 T ( z , t ) —, x 8 T ( z , t )) „      8 ( „ ,— ₂, _x —₂, _xxd T ( z , t ))

(R2 (z,t)-R1 (z,t))l— ---+ V(z,t)— ----IPCp =— l ^Зф(R2 (z,t)-R1 (z,t))— ----IV dt              8z ) F 8z V

• -2 R1( z, t )V1 + R1'2( z, t)аг(Г (z, t) - T„) -

• - 2 R 2 ( z , t )V1 + R 2 ’ 2 ( z , t ) [ ® ₂ f n 2 ^ o (T ⁴ ( z , t ) - Tb ⁴ ) + a ₂ (T ( z , t )-T o )] +

• ₂                               . 1 ( p£ p T p ( n , t ) - S T ⁴( z , t ) )( ( R p - R 2 ( z , t )) + | R 2 ( z , t )|( z - n ) )

+ 4 n> 0 R 2 ( z , t ) R p ( R p - R 2 ( z , t ) ) I ^p^ -2¹------ Цn ,

0                  ( ^{( n - z} )^{2 + ( R} p ^{- R} 2^{( z} , t ))² )

V ( z ,0) = V_s ( z ), V (0, t ) = V o , V ( L , t ) = V l

^R 1⁽ z ^,0) = ^R 1 _s ⁽ z ), ^R 1^(0, t ) = ^R 10

R 2 ( z ,0) = R 2 _s ( z ), R 2 (0, t ) = R 20

T ( z ,0) = T s ( z ), T (0, t ) = T 0 , ^| z = L = 0

L                                  8 z

Здесь z - продольная координата, z e [ 0, L ] ; t - время; R ₂( z , t ) - внешний радиус капилляра; R ₁( z , t ) – внутренний радиус капилляра; V ( z , t ) – скорость течения расплава; T ( z , t ) - температура расплава; м(T ( z , t )) - вязкость расплава кварца; T_p(z,t),T_e,T_n,T₀ -соответственно, температура печи, газа внутри и снаружи трубы, температура окружающей среды; A T , Х _э ф - коэффициенты молекулярной теплопроводности расплава и эффективный, учитывающий как молекулярную, так и лучистую проводимость; в -коэффициент отражения; е _P , е - степень черноты нагревательного элемента и расплава; с , C p -плотность и удельная тепловодность расплава соответственно; г - коэффициент поверхностного натяжения; а ₁, а ₂ - коэффициенты теплоотдачи с внутренней и внешней поверхности печи; P ₀ – разность между внутренним и внешним давлениями; R_p – радиус печи; V ₀, V_L – скорость подачи и вытяжки волокна; V_s ( z ), R _{1 s} ( z ), R _{2 s} ( z ), T_s ( z ) – функции, соответствующие начальному состоянию системы; R ₁₀, R ₂₀, T ₀ – соответственно, внутренний и внешний радиусы заготовки и ее температура.

Обезразмерим данную систему следующим образом [3; 5]:

z - z , t - VR_V ( z , t ) = V^zt) , ^ ( z , t ) = R^t) , R ( z , t ) = R 2 ( zt ), T ( z , t ) = Tzt ),

L L         VL            L             LT

. _ ^ё эф _ ^Ц

Z -

A)

В результате система примет вид д V (z, t)          д V (z, t))

( R 2 ²( z , t ) - R 1 ²( z , t )) l            + V ( z , t )             Il д t              д z )

• 3    д f„ _{2          2}, _xx д V ( z , t ) )

• ^- I ^{( R} 2 ^{( z} , t ) - ^R 1 ^{( z} , t ^{)) ц}          I ⁺

Re д z l                       д z )

• ₊ ( R 2 ²( z , t ) - R 1 ²( z , t )) ₊ 1 д ( R 1 ( z , t ) + R 2 ( z , t )) Fr          We        д z        '

  д R i ²( z , t ) + д ( V ( z , t ) R i²( z , t ))

  
  

  д t

  
  

  д z

  
  

  д R ₂²( z , t ) д ( V ( z , t ) R ₂²( z , t ))

  
  

  ^LaR 1 ^{2 ( z} , t ) ^R 2 ^{2 ( z} , t ) - -1- ^R 1^{( z} , t ) R 2 ( z , t ) ( R 1 ( z , t ) + R 2 ( z , t )) Ma

  ц ( R 2 ²( z , t ) - R 1 ²( z , t ))                      ,

  LaR 1 ² ( z , t ) R 2 ² ( z , t ) - -1- R 1 ( z , t ) R 2 ( z , t ) ( R 1 ( z , t ) + R 2 ( z , t )) Ma

  
  

  д t

  
  

  д z

  
  

  ц ( R 2 ² - R 1 ²)

  
  

. _{2          2/}   wf д T ( z , t )           д T ( z , t ) )    1 д (      _{2           2},    _ххд T ( z , t )

-

(R2 (z,t)-Ri (z,t))l — ----+ V(z,t)— ----I        I Z(R2 (z,t)-Ri (z,t))—;---- l   д t               дz   ) Pe дz l                          дz

^

-

-

- 2 R i ( z , t )V1 + R i' ²( z , t ) St i (T ( z , t ) -T n ) - 2 R 2 ( z , t )^1 + R 2 2 ( z , t ) St₂ (T ( z , t ) - 1 ) - - 2 _{Z r}R 2 ( z , t )V1 + R 2 2 ( z , t ) St 2 (T ⁴( z , t ) - Tb ⁴ ) +

• , _x ,         ,   _xX 1 ( PS p T p ( n , t ) - f T ⁴( z , t ) )( ( R - R 2 ( z , t )) + k\

+ 4 X 2 R 2 ( z , t ) R p ( R p - R 2 ( z , t ) ) I                                -------------- -2

din ,

0                  ( ^{( n - z )2 + ( R} p ^{- R} 2⁽ z , t ⁾⁾² )

• V ( z ,0) - V s ^z) , V (0, t ) --, V ( L , t ) - 1 V L           E

, x ^R 1 S ⁽ z )       / x R 10

R 1 ( z ,0) - ——, R 1 (0, t ) - -^-

„ , x ^R 2 s ^{( z} )    „ z x R ₂o

R 2( z ,0) - ——, R 2(0, t ) - - L 2.

T ( z ,0) - T s ^z) , T (0, t ) - T ⁰, | T | z _{= L} - 0

^T 0             ^T 0    ^{д z}

ñVL где Re ------ Ц p  PCPVLL бера; Pe ---------

. V,2

• -    число Рейнольдса; Fr ---- - число Фруда; We ------- - число Ве-

• L^ з        2 з

2      3           23

to 2 S n , <7 0 ^T 0         n c G 0 ^T 0

• -    число Пекле; X ----------, X ------ — безразмерные ком-

• pCpVL       pCpVL

Математический анализ устойчивости неизотермической вытяжки полого волокна

а         а                        PL      Ио VI.

плексы; St =------, St, =------ - критерий Стэнтона; La =-----, Ma =---- - крите- pCpv о       pCpv о                           м о Vl        г рий взаимодействия капиллярных сил и сил молекулярного трения соответственно.

Стационарное решение неизотермического процесса вытяжки полого волокна

Для дальнейшего анализа устойчивости необходимо найти решение соответствующей стационарной системы, которая имеет вид

( R 22 ( ^z ) ^- R 12⁽ z )) f V ⁽ z ) d^{V (} z ) ) = I dz )

=3т ■ df (R22( z) - R12( z ))^dV(z) d Re dz ^

( R 22 ( z ) - R 12 ( z ))    1 d ( R 1 ( z ) + R 2 ( z ))

+---1

FrWe

d(V ( z ) R 2 ( z )) LaR 1 ² ( z ) R 2 ² ( z ) - M R 1 ( z ) R 2 ( z ) ( R 1 ( z ) ⁺ R 2 ( z ))

dz       =                d R 22( z) - R 12( z))’

_d ( V ( _z ) R 2 ( _z )) LaR 12 ( z ) R 22 ( z ) - M R 1 ( z ) R 2 ( z ) ( R 1 ( z ) + R 2 ( z ))

dz      ⁼                d R 22 ( z ) - R 12 ( z ))

(R22 (z) - R12 (z ))f V (z) d™) = ——f 2( R 22 (z) - R12 (z)) dT(z) ) -( dz ) Pe dz (

• - 2 R 1 ( z )V1 + R i' ²( z ) St i (T ( z )-T „ ) - 2 R 2 ( z )д/1 + R 2 2 ( z ) St₂ (T ( z ) - 1 ) -

  
  

• - 2 X 1 R 2 ( z )V1 + R 22 ( z ) St 2 (T ⁴( z ) - Tb ⁴ ) +

  + 4 X 2 R 2 ( z ) R p ( R p

  
  
  

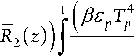
  - S T ⁴( ^ ) )( ( R_p - R 2 ( z )) + k|R 2 ( z )|( z - n ) )

  ----------- ------------------2

( ( П - z )² + ( R p - R 2 ( z ))² )

V (0) = |, V ( L ) = 1

E

R 1 (0) = RL°-

R 2 (0) = RL¹

^T (0) = Th dT | z = L = 0

T ₀    dz

Здесь V ( z ), R ₁( z ), R ₂( z ), T ( z ) – параметры стационарного течения, к которому стремится реальный процесс. Именно это состояние в дальнейшем будет исследовано на устойчивость.

Математическая модель устойчивости неизотермического процесса вытяжки полого волокна

Известно, что если какая-то нелинейная система линеаризована в окрестности своего стационарного состояния, то анализ такой линеаризованной системы может заменить анализ исходной системы [8].

Соответственно, на первом этапе была выполнена линеаризация: определяющие состояние системы параметры разделялись на основные и возмущающие:

V ( z , t ) = V ( z ) [ 1 + V ( z , t ) ] ;

T ( Z , t ) = T ( Z ) [ 1 + T ( z , t ) ] ;

R 1 ( Z , t ) = R 1 ( Z ) [ 1 + R 1 ( Z , t ) ] ;

R 2 ( Z , t ) = R 2 ( Z ) [ 1 + R 2 ( Z , t ) ] .

В роли основных параметров выступает стационарные решения системы (3). В результате была получена система, описывающая эволюцию возмущающих воздействий. Для упрощения записи всюду далее

V ( z , t ) = V ^- , T ( z , t ) = T , И 1 ( z , t ) = R 1 , R - ( z , t ) = R 2 ,

V ( z ) = V , T ( z ) = T , R 1 ( z ) = R 1 , R 2 ( z ) = R 2 ;

*v av

+ Д( Z ) — + Д( Z ) V d z

a V - = 3 a V ^- d t ” Re a z z

—w-

, _x ai^-                        a r,

⁺ « 1⁽ Z ) — ^{+ a} 2⁽ Z ) ^R 2 + ⁹ 1⁽ Z ) — d z                  d z

^{+ 9} 2^{( Z} ) R ^{- +} ^ 1^{( Z} ) — ⁺ Ф 2 ^{( Z),T} , a z

—w-

^R . + в з ( Z ) d V + в 4 ( Z)V + d t         d z

_ , X d R l            ~        Z X ~

” ^{+ 9} 3^{( Z} )^    ^{+ 9} 4^{( Z} ) ^R 1 ^{+ a} 3^{( Z} ) ^R 2

a Z

= 0,

—w-

R lr ^{+ в} 3⁽ Z ) | V + ^в 5⁽ Z ^)V + d t          d z

^{+ 9} 3^{( Z} )^"^" ^{+ 9} 5^{( Z} ) - R 1 ^{+ a} 4^{( Z} ) - R 2 d z

= 0,

a t = x a t a t ~ Pe a z z-

—w-

—w-

/ x d t                 d r₂

⁺ Ф з ^{( Z} )— ⁺ Ф 4 ^{( Z )T +} « 5 ^{( Z} )—

0 z                 d z

—•—

d R

a r.

+« б ( z ) R 2 + 9 6 ( x )   ¹ + ^ 7 ( z ) R1 + в б ( Z ) V ^.

a x

Соответствующие коэффициенты зависят только от стационарного решения исходной системы:

_x 6 м V' R,² а ( z ) = -   _2 +

R 2

We V R ^{2 ,}

• ¹    V Re R ²

  Математический анализ устойчивости неизотермической вытяжки полого волокна

  
  

  ^a 2⁽ z ) =

  
  

  - 2 R 2 ²

  
  

  d

  
  

  R ²

  
  

  2 dV |+ ^{2 R} 2

  ² dz V VFrR²

  
  

  +

  
  

  R 2'_

  We V R ^{2 ,}

  
  

  Р 1⁽ z ) =

  
  

  R ² V Re dz

  Re VR ²

  

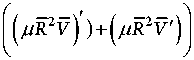
  - V ,

  d

  ( m R ² V ') - 2 V',

  
  

  ^в 2⁽ z ) =

  
  
  
  

  Re VR ² dx

  
  

  _д    = -6 R i ² V'M     R

  ¹      R ² V Re    WeVR ²

  
  

  ^ 2⁽ z ) =

  
  

  - 6

  
  

  d

  
  

  R ² V Re dx

  
  

  2 dV I A R i — 1 + dx )

  
  

  2 V* R 12

  
  

  R ²

  
  

  _-

  
  

  2 R ₁ ²

  ---=2 ⁺

  VFr R ²

  
  

  R i'_

  We V R ^{2 ,}

  
  

  Ф 1 ( z ) =

  
  

  _-

  
  

  3 a ₂ A TV'

  Re V ^,

  
  

  Ф 2 ( Z ) =

  
  
  
  

  d

  
  

  _-

  
  

  Re R ² Vdx

  
  

  2 dV

  3 ц а ₂ TR

  dx

  
  

  ^e 3^{( z} ) = V^>

  
  

  ^в 4^{( z} ) =

  
  
  
  

  d

  
  

  2 R ₁ ² dx

  
  

  ( R 12 v ) ,

  
  

  ^ з ( Z ) = V ,

  
  

  @ 4^{( z} ) =

  
  

  1 d

  
  

  R ₁ 2 dx

  
  

  ( R 12 V ) -

  
  

  —— X

  2 R ₁

  
  

  X

  
  

  ^2

  2 La R 1 R ₂

  
  

  _-

  
  

  2 _RR

  Ma ¹²

  AR²

  
  

  _-

  
  

  1 _R 2 Ma ²

  
  

  2 R 1 1 LaR 1 ² R ₂ ²

  
  

  _-

  
  

  A

  
  

  V

  
  

  ^a 3^{( z} ) =

  
  

  _-

  
  

  R 2 2 R ₁ ²

  
  

  2 La R ₁ ² R ₂

  
  

  _-

  
  

  _-

  
  

  A R 12

  
  

  _-

  
  

  R 2 ²)²

  
  

  ^,

  
  

  V

  
  

  R ₂

  ⁺ - ₂

  2 R ₁ ²

  
  

  2 R 2 I LaR i ² R 22

  
  

  _-

  
  

  A R 1 ²

  
  

  _-

  
  

  V

  
  

  ^в 5^{( z} ) =

  
  
  
  

  d

  
  

  2 R ₂ ² dz

  
  

  ( R 22 V ) ,

  
  

  2 _RR

  Ma ¹²

  m R ²

  
  

  R 2 ²)²

  
  

  _-

  
  

  1 _R 2 Ma ¹

  
  

  +

  
  

  A

  
  

  V

  
  

^a 4⁽ z ) = R 22 dz ( ^R 22 V )

2 R ₂

⁶ 5⁽ z ) =

-

R 1

2 R 2 ²

2 LaR ² R —— R, R - — R ,²

^{1  2} Ma ¹² Ma ¹

M R ²

(             1             ^11

2 R 2 La Ry R 2-- R i R 2 ( R i + R 2)

² к ¹    2 Ma 2' ^{1    2} )

m ( r 1 ² - R 2 ) ²

-

R 1

2 R 2 ²

2 La R ₁ R ₂ ²

2 R 1 1 LaR 1 ² R ₂ ²

-

-

2 R 1 R

Ma

M R ²

m ( r 1 ² - R 2 ) ²

-

¹ R 2 ²

Ma

-

,

'

Ф з^{( z} )

( A R ² T ) + A R ² T' _

=-— 4=-- v ,

R ² TPe

- 8 R 2 T ⁴V1 + R 2 ² X i

- VR ²

dT -16 _Z R p S (R p - R 2) T ⁴ j-

^R p ^{- R} 2 ⁺ k ^R 2 ⁽ z - ^{n )}

^{( n -} z ^{) 2 +} ( ^R p ^{- R} 2 )

^dn ),

VT' в б ( z ) = - VT ,

« 5 (z ) =

^(|- d f A R 2 ² dT ^- 2 R 2 R 2 ² St 2 ( T - 1) - 2 R 2 R 2 ² ( T ⁴ - T b ⁴) X1 + R ² T ee dz к dz )                            ^{v        2}

+ 4 X 2 R p R 2 ² ( R p - R 2 ) k j ^^Pe p ^{T p}

^- S T ^{4 )(} z ^- n )

( П - z )² + ( R p - R )

d n ),

Математический анализ устойчивости неизотермической вытяжки полого волокна a (z)=-=1=- (——I xr22 — I - 2R2 t(1+3R‘2) st2 (t - 1) -

• ⁶       R ² T ^ee dz I ² dz )      ²      2 ²     2

  - 2 R 2 (T ⁴ - T b ⁴)(1 + 2 R 2 ²) X i

  
  

  - 2 VR 22

  
  

  dT dz

  
  

  + 4 X 2 R p R 2 ^М - _ет 4 ) 0

  
  

  ( R p - R 2 )( R p - 3 R 2 ) + kR 2 ( z - n ) ( R p - 2 R 2 )

  
  

  [ ( n - z )² + ( R p - R 2 )² ] ²

  
  

  +

  
  

  +

  
  

( 4 R 2 ) ( R p - R 2 ) ( R p - R 2 + kR 2 ( z -n )) ^{[ ( n -} z ^{) 2 + ( R} p ^{- R} 2^{) 2} ]

d n ),

6 7 ( z ) = -=1=- ^[ - -2- ^{— 1 X R} 1 ^{2 —T 1} - 2 St 1 ^R 1 ( ^T - ^T H ) f ¹ + 3 ^R 1 ² 1 + ² VR 1 ^{2 dT} . R ² T ee dz ^ dz )        ^x \    2    )         dz

Здесь R ² = R 1 ² - R ₂².

На следующем этапе был применен метод разделения переменных [5; 6], а именно выполнена замена:

R 1 ( z, т ) = Г 1 ( z ) e i ®^T ;

^R 2^{( z , t )} = Г 2^{( z} )e - ® ;

T ( z , t ) = t ( z ) e - ' ;

V ( z , t ) = v ( z ) e - i ®^T .

В результате была получена система линейных обыкновенных дифференциальных уравнений:

3 ^ v "( ^z ) ⁺ A ^{( z} ) v ' ( ^z ) ^{+ [ e} 2 ⁽ z ) ⁺ i ® ^] v ⁽ z ) ^{+ a} 1 ⁽ z ) r 2 ⁽ z ) ^{+ a} 2 ⁽ x ) ^r 2 ⁽ z ) ⁺ Re

^{+ 6} 1 ^{( z} ) r /^{( z} ) + 0 2 ⁽ z ) Г 1 ⁽ z ) + Ф 1 ⁽ z ) t '( z ) + ^ 2 ^{( z} ) t ^{( z} ) = 0,

Р з ⁽ z ) v ' ⁽ z ) ^{+ в} 4 ⁽ z ^{) v (} z ) ^{+ 0} 3 ⁽ z M z ) ^{+ ( 0} 4 ⁽ z ) ^- i ® )r 1 ⁽ z ) ^{+ a} 3 ⁽ z ) r 2 ⁽ z ) = 0, ^в 3 ⁽ z ) v ' ⁽ z ) ^{+ в} 5 ⁽ z ) v ⁽ z ) ^{+ 0} 3 ⁽ z ) ^r 2 ^{( z} ) ^{+ ( a} 4 ^{( z} ) ^- i ® ^)r2 ^{( z} ) ^{+ 0} 5 ^{( z ) r} 1 ^{( z} ) = 0, X

— t "( ^z ) + Ф з ^{( z} )t '( ^z ) + ⁽ Ф 4 ^{( z} ) + i ® )t ^{( z} ) + ^a 5 ^{( z} ) r ‘ ^{( z} ) + « 6 ^{( z} ) ^r 2 ^{( z} ) + ^e e

^{+ 0} 6 ^{( z ) r} 1'^{( z} ) ^{+ 0} 7 ^{( z} ) ^r 1 ^{( z} ) ⁺ Р б ^{( z} ) v ^{( z} ) = ⁰

С помощью дискретизации конечно-разностным методом (центральная аппроксимация) перейдем к системе линейных алгебраических уравнений.

В матричном виде система имеет вид

( iA - ® E ) X = 0,

Г v k )

r1 k r2 k

. t k >

где E - единичная матрица; А - матрица коэффициентов при переменных; X = – вектор-столбец значений переменных на каждом шаге.

Стоит отметить, что размерность вышеперечисленных матриц зависит от количества узлов, выбранного при дискретизации системы (4).

По матричной форме видно, что to являются собственными значениям матрицы коэффициентов А. Так как собственная частота является комплексным числом, то to = to ₂ + i to i , где to i - коэффициент нарастания. Именно этот коэффициент позволяет судить о том, затухают или нарастают колебания. Если все to i <  0, можно говорить, что колебания затухают, значит, исследуемое состояние (стационарное течение) устойчиво, при to i >  0 - неустойчиво [5; 6]. Тем самым задача анализа устойчивости свелась к задаче на собственные числа матрицы коэффициентов. При этом стоит отметить, что для определения устойчивости достаточно оценивать только максимальное значение мнимой части to^ .

В качестве примера сформулируем алгоритм заполнения матрицы А в случаи числа точек дискретизации 3 и, соответственно, количество уравнений – 12.

Коэффициенты при
v 1	r 11	r 21	t 1	v 2	r 12	r 22	t 2	v 3	r 13	r 23	t 3
V 11	R 111	R 121	T 11	VVV 1	0	0	0	0	0	0	0
V 21	R 211	R 221	0	0	0	0	0	0	0	0	0
V 31	R 311	R 321	0	0	0	0	0	0	0	0	0
V 41	R 411	R 421	T 41	0	0	0	TTT 1	0	0	0	0
VV 11	RR 111	RR 121	TT 11	V 12	R 112	R 122	T 12	VVV 2	0	0	0
VV 21	RR 221	0	0	V 22	R 212	R 222	0	0	0	0	0
VV 21	0	RR 221	0	V 32	R 312	R 322	0	0	0	0	0
0	RR 411	RR 421	TT 41	V 42	R 412	R 422	T 42	0	0	0	TTT 2
0	0	0	0	VV 12	RR 112	RR 122	TT 12	V 13	R 113	R 123	T 13
0	0	0	0	VV 22	RR 222	0	0	V 23	R 213	R 223	0
0	0	0	0	VV 22	0	RR 222	0	V 33	R 313	R 323	0
0	0	0	0	0	RR 412	RR 422	TT 42	V 43	R 413	R 423	T 43

3 и 1            X

Здесь VW₄ =        ; TTT, =      ;

ⁱ Re H ^{2 i}PeH ²

Математический анализ устойчивости неизотермической вытяжки полого волокна

1 i

6 µ 1

Re H ²

+ _H ^{1 i} + β _{2 i} ; R _{11 i}

= θ ¹ + θ

1 i H 2 i

R12i=1i+α2i;T1i=ϕ1i+ϕ2i;V2i=-3i-

R _{21 i} = - θ _{3 iH} - θ _{4 i} ; R _{22 i} =- α _{3 i} ; V _{3 i} =- α _{5 i} ;

θ 3 i

R _{31 i} =- θ _{5 i} ; R _{32 i} =- _H - α _{4 i} ; V _{4 i} =- β _{6 i} ;

11λϕ

R41i=θ6i+θ7i;R42i=α5i+α6i;T4i=-     2 ++

HHPeH H

^VV 1 i ⁼

3 µ 1

Re H ²

β1i1

; RR _{11 i} =- θ _{1 i} ; RR _{12 i} =- ;

HHH

ϕβ1

TT 1 i =- _H ^{1 i} ; VV 2 i = _H ^{3 i} ; RR 22 i = θ 3 i _H ; RR 41 i = _H ^{6 i} ;

αλ

ϕ _{3 i} H ^;

RR =- ^{5 i} ; TT = 42 i H 4 i PeH 2

Н – длина шага дискретизации.

Заключение

Одним из главных этапов производства оптического волокна является его вытяжка. Анализ устойчивости данного процесса необходим для обеспечения качества готового продукта. В данной работе построена модель устойчивости вытяжки полого волокна в условиях не-изотермичности: рассмотрена система, описывающая технологический процесс производства в мерном и обезразмеренном виде. Проведена линеаризация в окрестности стационарного решения и дискретизация конечно-разностным методом полученной системы. Задача определения устойчивости сведена к задаче на собственные числа матрицы коэффициентов. Вид и алгоритм формирования матрицы также сформулирован в данной работе.