МАТЕМАТИЧЕСКИЙ АППАРАТ АНАЛИЗА МОДЕЛЕЙ ДЛЯ 3D-ПЕЧАТИ

В статье проведен анализ факторов, влияющих на процесс 3D-печати по технологии послойного наплавления (FDM). Также рассматриваются возможности улучшения качества поверхности путем уменьшения "ступенчатости" поверхности изготавливаемого изделия. Описывается математический аппарат для оценки ориентации модели в рабочей области 3D-принтера, что позволит оптимизировать процесс 3D-печати по технологии послойного наплавления и расширить область применения этой технологии.

Кл. сл. : 3D-печать, математический аппарат, технология наплавления термопластов, качество поверхности

ТЕХНОЛОГИИ 3D-ПЕЧАТИ

3D-печать тесно вошла во многие области нашей жизни [1, 2]. В настоящее время все производители оборудования для 3D-печати идут по пути повышения качества, точности изготавливаемых прототипов и скорости изготовления, что в свою очередь, как правило, приводит к увеличению стоимости конечного изделия.

В настоящее время основными технологиями 3D-печати являются [3]:

• •    стереолитография;

• •    спекание;

• •    ламинирование;

• •    наплавление (FDM, FFF).

Наиболее доступной и распространенной является технология наплавления в связи с широким ассортиментом оборудования при относительно низкой стоимости самого оборудования и расходных материалов. Помимо этого, как правило, не требуется дополнительного оборудования для постобработки изготовленных деталей и специализированной подготовки персонала для работы с указанным типом оборудования и его обслуживания, что также снижает стоимость внедрения и использования этой технологии.

Так, стоимость 3D-принтера, работающего по технологии стереолитографии с толщиной слоя 16 мкм, может достигать 15 млн руб. и больше, в то же время стоимость оборудования для работы по технологии наплавления с толщиной слоя 0.1 мм находится на уровне от нескольких десятков до нескольких сотен тысяч рублей.

При использовании 3D-принтера с более крупным шагом печати возникает вопрос точности воспроизведения геометрии и качества поверхно- сти конечного изделия. Корректное расположение модели в рабочей области 3D-принтера может частично компенсировать недостатки, связанные с изготовлением модели по слоям. Для простых 3D-моделей ориентирование модели достаточно очевидно для опытного оператора 3D-принтера, однако для сложных моделей ориентирование становится непростой задачей [4].

Прежде чем приступить к ориентированию модели, нужно сформировать необходимый математический аппарат для анализа 3D-моделей и формализовать критерии оценки ориентации.

ТЕХНОЛОГИЯ НАПЛАВЛЕНИЯ

В связи с быстрыми темпами развития технологий 3D-печати, на рынке представлен широкий ассортимент оборудования и материалов для работы по технологиям FDM и FFF.

Достоинства:

• •    высокая скорость печати;

• •    низкая стоимость расходных материалов;

• •    широкая область применения;

• •    низкие требования к квалификации персонала.

Недостатки:

• •    низкое качество сложных моделей;

• •    низкая точность;

• •    малая прочность.

Основными параметрами, влияющими на качество изготавливаемого объекта, являются:

• •    количество и скорость проходов экструдера;

• •    глубина и скорость перемещения платформы;

• •    толщина слоя;

  

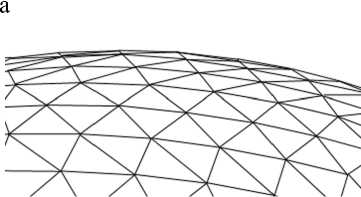
  Рис. 1. О п исание объе к та в STL-файле: а — аппроксимация поверхности треугольниками, б — проф и л ь

  
  
  
  
  

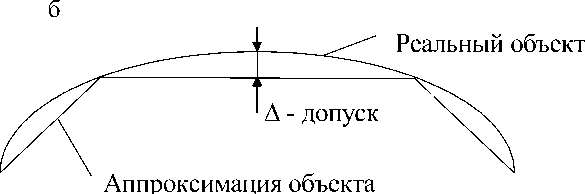
• •    отсутст в и е ош ибок в STL-файле;

• •    ра б очие те мпера ту ры;

• •    с к орост ь подачи ма т ериа л а ;

• •    ме х ан и к а 3D-принтера ;

• •    у с ад к а мате ри а л а;

• •    ориентация об ъ екта в ра б оче й зон е 3D-прин- т ера.

Помимо особ е н н остей самой технологии 3 D- п е ча ти , также необ х одимо обр а тит ь вн и мание н а форма т ф а й л ов, опи с ывающ и х гео ме три ю 3 D- м оде л и.

STL-ФОРМАТ

Основным форматом, используемым в качестве входных данных для автоматизированных систем технологической подготовки производства (АСТПП) в сфере 3D-печати, является STL-фор- мат, описывающий трехмерное компьютерное представление изготавливаемого объекта [5]. Этот формат описывает поверхность модели набором треугольников (рис. 1). Информация о треугольниках записывается перечнем координат каждой вершины треугольника и направлением нормали. Данные хранятся в виде текста (ASCII) или в двоичном формате.

Т очно с ть и ка ч ест в о к онечн ого изделия в о многом зависят от величины допуска.

В с в я зи с те м, что п ов е р хность описы в а е тс я н абором треугольников, в STL-файле воз мож ны ош и б к и, которые н е п оз в ол я т п ра ви ль но р а ботать ра зр абатываемой с и с те ме ори е нт а ц и е й о б ъ е к та в рабочей зоне 3D- п ри н те ра и ге нери ров а ть к орректный управляющий G-код. К таки м ошибк а м относятся незамкнутый контур (рис. 2, 3) и неверная ориентация треугольников (рис. 4, 5).

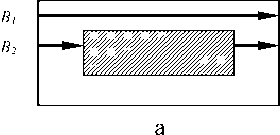
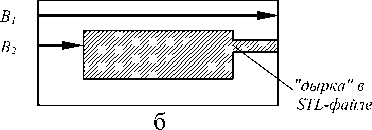
Рис. 2. Н е з а мк н утый к он тур. а — тре б у е м ое , б — ошиб о ч н ое

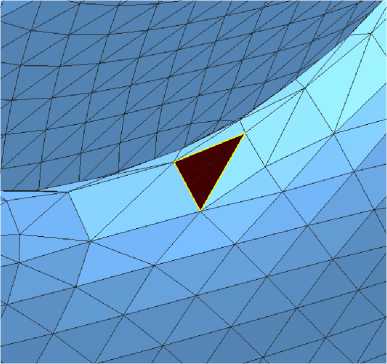
Рис. 3. О тс ут ст в ую щ ий треуг ол ь н ик

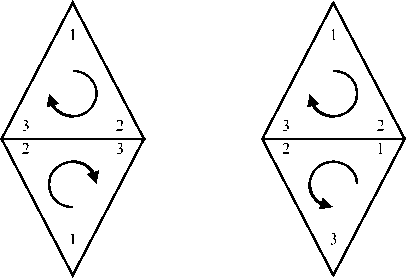
б

а

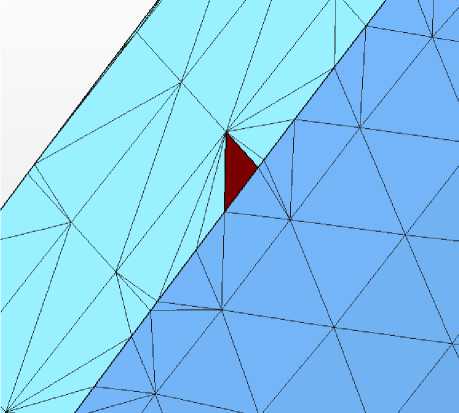
Рис. 5. Перевернутый треугольник

Рис. 4. Ориентаци я тр еу г о л ь ни ко в. а — тр ебу емая, б — о ш ибочная

Влиян ие ук аз анны х ошибок на процесс изго т ов лен ия и з д ел ия сил ьно з ависит от алг орит мов раб от ы А С Т ПП [6]. В с в язи с э т им в раз раб аты в аемой системе ори ентировани я 3D-моделей не об ход и мо п ред у см от реть об н ару ж ени е таких оши б ок и п ред у п реж д ать операт ора о их нал и чии в обрабаты в аемом ST L -файле.

ВНЕСЕНИЕ ПОГРЕШНОСТЕЙ

Основные погрешности вносятся на этапе экспорта моделей из САПР для твердотельного про- ектирования в STL-формат в связи с особенностями данного формата и на этапе технологической подготовки производства в связи с ориентацией объекта, толщиной слоя и его аппроксимацией при разбиении на слои (рис. 6). Ограничения на суммарные погрешности позволяют обеспечивать точность до 0.1 мм в конечном изделии. Помимо этого, очевидно, что аппроксимация горизонтальных, вертикальных стенок и близких к вертикальным (рис. 7) будет вносить меньшую погрешность, чем аппроксимация поверхностей с уклоном (рис. 8).

а

б

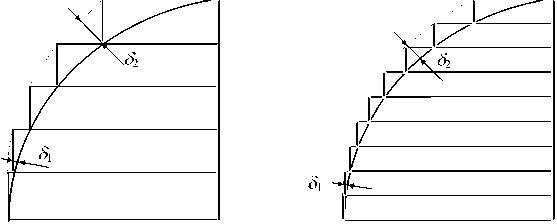
Рис. 6. Влияние толщины слоя на точность изделия.

а — "толстые" слои, б — "т онки е" сл ои

Рис. 7. Вертикальная поверхность напечатанного изделия под микроскопом

Рис. 8. П о верхн ост ь с уклоно м напечатанн о г о из д ел ия по д ми кр оскоп ом

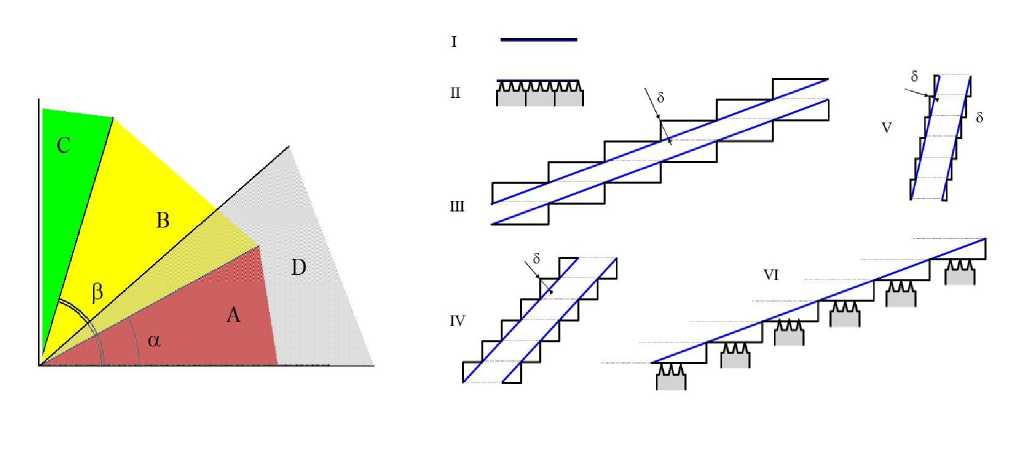
Рис. 9. Зоны качества и зона поддержек.

Моделируемые поверхности типа I, II, V относим к зоне С (оптимальное качество); поверхности с наклоном типа III — к зоне А (наихудшее качество); типа IV — к зоне B (среднее качество); "висячие" конструкции типа VI — к зоне D (требуют вспомогательных опор)

Из этого следует, что, сориентировав деталь таким образом, чтобы максимальное количество стенок имели горизонтальное, вертикальное или близкое к вертикальному положение, можно минимизировать погрешности геометрии полученного изделия относительно геометрии эталонной модели 3D-объекта, а также минимизировать количество элементов, для которых будут строиться поддерживающие структуры [7].

Таким образом, можно выделить 3 зоны качества поверхности по критерию "ступенчатости" — A, B и C (рис. 9):

• •    зона A — наихудшее;

• •    зона B — среднее;

• •    зона C — оптимальное качество.

Помимо трех зон качества выделяется зона D, в которой строятся вспомогательные элементы "поддержки". Части объекта, которые оказываются в этой зоне, нуждаются в дополнительной механической обработке, что в свою очередь также снижает качество поверхности [8].

В результате путем оценки соотношения площадей поверхности, принадлежащих к той или иной зоне, к общей площади поверхности модели можно сделать выводы об оптимальности ориентации модели в рабочей зоне 3D-принтера.

МАТЕМАТИЧЕСКИЙ АППАРАТ АНАЛИЗА МОДЕЛЕЙ ДЛЯ 3D-ПЕЧАТИ

Изделия для 3D-печати часто имеют сложную форму, и определить наилучшую ориентацию с точки зрения качества поверхностей бывает непросто. Для получения количественных характеристик качества ориентации необходимо создать математический аппарат для анализа исходного файла изделия (STL-файла). Прежде всего нас будут интересовать габаритные размеры, объем детали и наклон элементов ее поверхности. Поскольку модель изделия состоит из набора треугольников, то можно проводить анализ каждого элемента в отдельности и затем объединять полученные результаты. Необходимо определять габаритные размеры изделия и характеристики, требуемые для проведения оценки влияния ориентации на качество поверхности изделия.

Вычисление габаритных размеров

Производится путем последовательного просмотра всех треугольников в исходном STL-файле и выделения минимального и максимального значений по каждой координате. Одновременно вычисляется объем модели:

N

V = z v ,              (1)

= 1

где N — количество треугольников, vi — объем усеченной призмы, основание которой — проекция i-го треугольника на плоскость XOY, а верхняя грань — сам треугольник. При этом vi будет положительным, если нормаль к этому треугольнику направлена в положительный октант (т.е. координата z единичного вектора, с началом в точке (0,0,0) и параллельного нормали треугольника, положительна), и отрицательным, если направлена в отрицательный [9].

z, + z^ + z,

V = 5 . ■ —---- ² ----³

i xoyi          3

x1 x2 x3 y1 y2 y3 1 1 1 z1 + z 2 + z 3

3—■ (2)

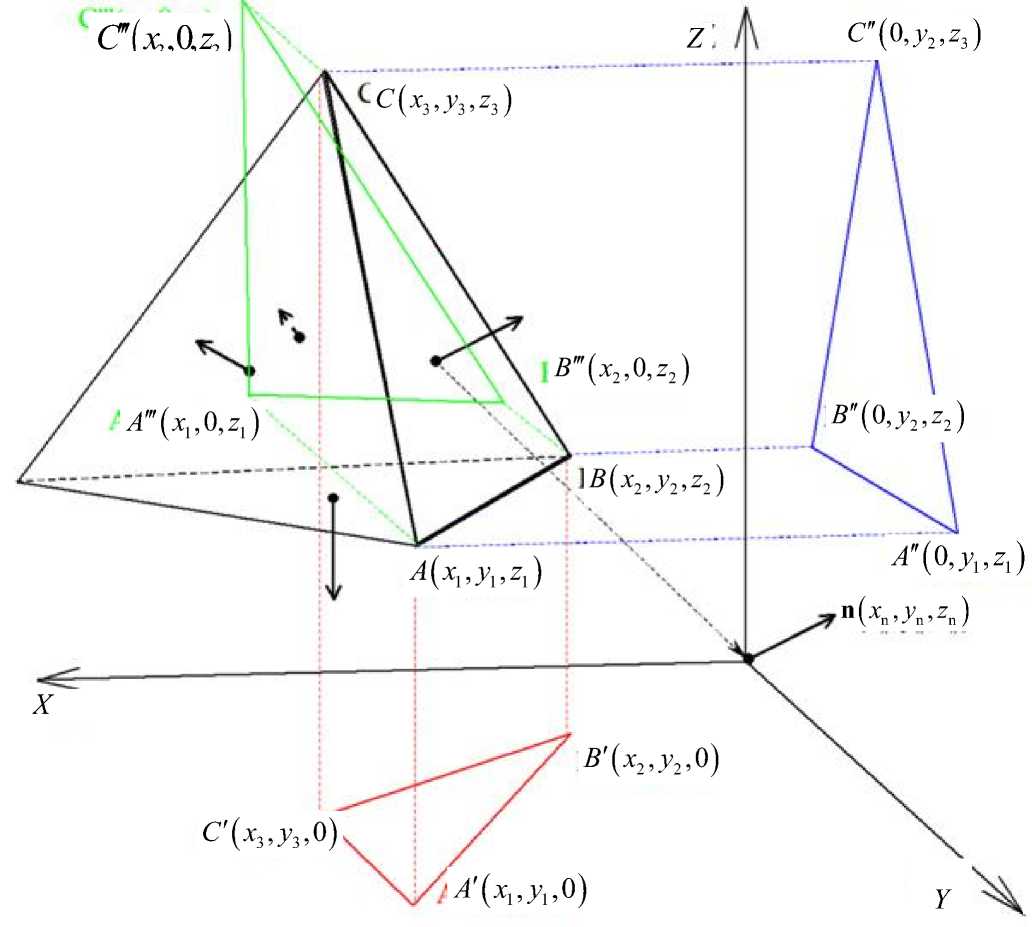
где ( x 1 , y 1 , z 1 ), ( x 2 , y 2 , z 2 ), ( x 3 , y 3 , z 3 ) — координаты вершин i -го треугольника, а s xoyi — площадь его проекции на плоскость XOY (рис. 10).

Z

X

Y

C '( x ₃

B ‘ ( x ₂

A'" ( x 1 ,0, z 1 )

B ”( X 2 ,0, z 2 )

A' ( x 1

^x i , У 1 , ^z i )

X 2 , У 2 , 2 2 )

A '‘( 0, У 1 , ^z 1 ) ( ^X n , У n , z n )

X 3 , У 3 , z 3 )

Рис. 10. Элемент поверхности модели и его проекции

Раскрытие определителя дает два вида результата:

xoyi

x_i y 2 + x 2 y 3 + x 3 y _i - x 3 y 2 - x 2 y _i - x_i y 3

₌ x i ( У 2 s xoyi

^- y 3 ) + x 2 ( y 3 - y ) + x 3 ( y - y 2 ) 2

S i = 2 J AB X AC ,             (ii)

	i	j	k
AB x AC =	x B1	y B1	z B1	.              (12)
	x B2	y B2	z B2

Формула (3) содержит 6 операций умножения и 5 операций сложения, формула (4) содержит 3 операции умножения и 5 операций сложения, следовательно, в связи с меньшим количеством действий вычисления по формуле (4) будут происходить быстрее.

Таким образом, объем модели:

N

Z v,

I = 1

v i = ( x i ( У 2 ^- У 3 ) ⁺ x 2 ( У 3 ^- y i ) ⁺ x 3 ( y i ^- У 2 ) ) ^{X     (5)}

x ( z_i + z 2 + z 3 ) /6;

габариты модели:

H = z max	— Z 1 min	(6)
А Y = У max	- y mm;	(7)

^ X = x max - x min .                                ⁽⁸⁾

Вычисление характеристик

Основные характеристики, которые нас интересуют, — площадь поверхности модели и отдельных ее элементов. В связи с тем, что некоторые САПР при экспорте модели в формат STL не рассчитывают нормали для треугольников, оставляя значения их компонент равными нулю, необходимо вычислять нормали треугольников на основе координат их вершин.

Поскольку поверхность описана набором треугольников, а точнее координатами их вершин, воспользуемся формулой вычисления площади треугольника в векторной форме.

Зная координаты вершин A ( x 1 , y 1 , z 1 ), B ( x 2 , y 2 , z ₂), C ( x ₃, y ₃, z ₃), найдем 2 вектора AB AB и AC :

Ab = b - a =

= ( x 2 ^- x l , У 2 ^- y i , z 2 ^- z i ) = ( x Bi , У Bi , z Bi ) ,    (9)

AC = C - A =

= ⁽ x 3 ^- x i , ^y 3 ^{- y} i , z 3 ^- z i ) = ⁽ x B2 , ^y B2 , ^z B2 ^{) .} (i0)

Площадь треугольника:

Раскрытие определителя дает результат:

^AB X ^AC = ^{( y} Bi • z B2   z Bi • ^y B2 ) • i ⁺

^{+ (} z Bi • x B2 x Bi • ^y B2 ) • j ^{+ (} x Bi • ^y B2 ^y Bi • x B2 ) • ^k. (i3)

Примем,        что        a = ybi • zB2 - zbi • yB2, b = zBi • xB2 - xBi • yB2 и c = xBi • yB2 - yBi • xB2 , тогДа:

AB x AC = a • i + b • j + c • k.(i4)

Итоговая формула площади треугольника:

si = i • V a2 + b2 + c2.(i5)

Площадь поверхности модели:

N s = Z Si,(i6)

i=i где N — количество треугольников.

Для вычисления нормали треугольника, как и в случ ае вычисл ен ия площади, нужно найти 2 вектора AB AB и AC . После этого нужно найти их векторное произведение по формуле (13). Найдя векторное произведение, получим вектор, который нужно нормировать для получения нормали. Нормирование вектора достигается путем деления каждой компоненты вектора на его длину.

Приняв по формуле (i3) x = y _Bi • z _B2 - z _Bi • y _B2, у = z Bi • x B2 - x Bi • у B2 и z = x Bi • у B2 - у Bi • x В2 ^,ПоЛУ— чим длину вектора:

L = 7 x ² + y ² + z ².                 (i 7)

Нормаль треугольника:

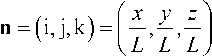
Исходя из значения компоненты k вектора нормали треугольника, можно определить, к какой из ранее определенных зон качества (рис. 9) принадлежит каждый треугольник, описывающий поверхность 3D-модели.

Поворачивая модель по осям OX и OY, можно влиять на принадлежность треугольников к зонам качества. Для пересчета координат вершин треугольников воспользуемся матрицами поворота. Для поворота по этим осям, соответственно, необходимы только 2 матрицы поворота.

Матрица поворота вокруг оси OX :

	' 1     0	0 ^
M x ( 9 ) =	0 cos θ к 0 sin 9	- sin 9 cos 9 j	.            (19)

Матрица поворота вокруг оси OY :

	^ cos 9	0	sin 9 ^
M , ( 9 ) =	0	1	0	.             (20)
	k- sin 9	0	cos 9 j

Соответственно, для поворота объекта вокруг оси OX или оси OY нужно умножить координаты вершин всех треугольников в модели на соответствующую матрицу. Тогда новые значения координат для вершины A с координатами ( x c , y c , z c ) после поворота по оси OX будут равны:

материала в процессе печати, существует время, необходимое на смену слоя при печати. Соответственно с увеличением высоты увеличивается количество наносимых слоев, а следовательно, увеличивается и суммарное время, необходимое на смену слоев [10].

Формализовав условия оптимальной ориентации модели в рабочей области 3D-принтера с точки зрения качества и точности поверхности изготавливаемой детали, получим следующие результаты:

• •    площадь элементов с (A <  k < 1) или (-1 <  k < < –A) → min;

• •    площадь элементов с ( k = 1) или (-B <  k < B) → max;

• •    площадь элементов с (-1 <  k < -C) ^ min;

• •    H ^ min, где H — высота модели.

На основании вышеизложенного можно получить функцию оценки ориентации модели в рабочей области 3D-принтера [11]:

Pm =

Г 1     0

( x n , У n , z n

) = ⁰ к 0

cos θ sin θ

0 '

- sin 9 • cos 9

' xc yc к z c 7

KcyNSc. -КдУХ. -КцУХ

C _i   C i      A _i A i      D _i D i

S

- ^ H , (25) max

Для облегчения автоматических расчетов будем основываться на компоненте k вектора нормали треугольника. Введем, согласно рис. 9, три константы, определяющие зоны: А, B и C. При этом:

A = cos a,

B = cos в,

C = cos y , (24)

α , β , γ — углы, определяемые пользователем: α — угол для зоны A, в которой качество поверхности элементов считается наихудшей, β — угол, начиная с которого качество поверхности элементов считается оптимальным, γ — угол для зоны D, в которой под элементы поверхности строятся поддержки.

В то же время желательно ориентировать модель таким образом, чтобы ее высота была минимальной, что позволяет добиться ее большей устойчивости на рабочей платформе во время печати и уменьшения количества слоев, а следовательно, и уменьшения количества ступеней на поверхности изготовленной детали. Также деталь, ориентация которой имеет минимальный размер по оси OZ , изготавливается быстрее. Это связано с тем фактом, что при неизменности площади поверхности модели в зависимости от ориентации и, следовательно, неизменности количества наносимого

где ρ m — функция оценки ориентации модели в рабочей области 3D-принтера, принимающая значения от –3 до 1 (–3 соответствует наихудшей ориентации, 1 — наилучшей). Здесь:

s A i , s C i , s D i — площадь i -го треугольника, принадлежащего зонам A, C и D соответственно, согласно рис. 9;

K A , K C , K D , K H — весовые коэффициенты для зон A, C, D и высоты модели соответственно, принимающие значения от 0 до 1 и зависящие от особенностей используемого оборудования и предпочтений оператора 3D-принтера;

H max , H m — наибольший габаритный размер 3D-модели и ее высота в выбранной ориентации.

ВЫВОДЫ

В статье описан разработанный математический аппарат анализа моделей для 3D-печати, который позволяет вычислить основные параметры 3D-модели в формате STL. Помимо этого, математический аппарат позволяет вычислять параметры отдельных элементов 3D-модели, такие как площадь и угол наклона к столу 3D-принтера. Также предложена функция оценки ориентации модели в рабочей области 3D-принтера. В дальнейшем предложенное решение можно использовать при разработке алгоритмов автоматического поиска оптимальной ориентации при разработке собственной АСТПП для 3D-печати.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации, номер темы FSFF-2020-0015.