Математический метод определения зерновых характеристик сыпучих материалов

Инвестиционно-строительная компания “Средневолжскстрой”

В статье дана математическая модель описания зерновых характеристик сыпучих строительных материалов. Предложены формулы для определения удельной поверхности числа частиц в единице массы и пористости. Правильность расчетов подтверждается практикой их использования в лабораторных условиях.

При изучении ряда процессов, происходящих в пористой среде, как-то: движение газов или жидкостей через слой, перепад давлений в неподвижном слое, переход неподвижного слоя в псевдоожиженное состояние, теплообмен в слое, скорость витания отдельных частиц и многих других практически важных задач, приходится определять гранулометрический состав сыпучего материала.

Обработка опытных данных по ситовому анализу керамзитового гравия и песка приводит к известному уравнению:

R x = 100 1 ^- bx n %,             (1)

где R_x – полный остаток на сите с размером отверстия х, мм; n и b – постоянные коэффициенты, зависящие от технологического процесса производства керамзитового гравия; l – основание натуральных логарифмов.

В уравнении (1) неизвестными являются константы n и b , которые можно определить, если произвести просеивание материала через два сита с отверстиями а₁ и а₂ мм. Из уравнения (1) получим:

R = 1001 - ban, a1

R = 1001"ba 2n.

a ₂

После логарифмирования имеем:

In R = ln100 - ban, a1

In Ra2 = ln100 - ba2n,

Из (4) находим:

1    100

b =-- In----.

a ₁ ⁿ     Ra ₁

Из (5) следует:

b = — • In

a

n

Ra ₂

Приравнивая уравнения (6) и (7), получаем:

' a 2 ) n = ln100 - In Ra 2 = 4,6052 - In Ra 2

_v a 1 ^J = ln100 - In Ra 1 = 4,6052 - In Ra 1 '

Вторичное логарифмирование дает:

, a, , 4,6052 - In Ra, n ln — = In-------------, a1     4,6052 - In Ra1

откуда

1      , 4,6052 - In Ra, n =--In-----------------.

In a ₂ - In a 1     4,6052 - In Ra 1

Зная полные остатки на ситах Ra₁ и Ra₂ , из выражения (8) определяется n , затем из (7) коэффициент b .

Подставляя найденные значения n и b в уравнение (2) можно подсчитать полные остатки на ситах для любых значений x .

Если в выражение (2) подставить значение b из (7), то после логарифмирования получим удобную для подсчетов формулу:

Ro,^ ( 100 J

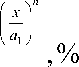
Если задаться максимальным размером зерна x_max , причем считать, как обычно, полный остаток на сите Rx_max =0,1%, то по формуле (9) получим:

до xmax можно записать:

Rx max

= 100

Ra-

V 100 J

x max

V a 1

A ⁿ

,

J

6 x max yd N =-- ^x y x ,

πγ x ³ x min

шт/кг.

откуда

( Ra1

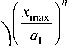
Функция y=f(x) определяет процент содержания в единице массы зерен определенного размера.

Подставляя вместо y его значения равное nbx^n-1 и полагая nbx^n-1=Z получим:

V 100 J

После логарифмирования находим:

- ln - 1000

Далее следует:

6,9078 =

откуда получаем:

x max

n

V ^a 1 J

x max

n

V a j

■ In Ra ¹ .

Ra

■ In

6,9078

x = a, ---------------- max   ^4,6052 - In Ra1

.

Зерновая характеристика материала по остаткам на ситах дает возможность определить, какое количество частиц данного размера х содержится в единице массы материала и процентное содержание частиц, лежащих в любом интервале от х₁ , до х₂ .

Теоретическое определение числа частиц в единице массы

Если принять, что частицы любого сыпучего материала имеют сферическую форму, то количество частиц, имеющих размер х , составляет:

nx

6 y

3 . πγ x

Общее числовое количество зерен в единице массы (1кг) составит:

N = n₁ + n 2 + n 3 + ... n_k

=_X k ni - A- X ! У , nY i = 1 x 3 i

шт/кг.

При непрерывном изменении х от xmin

6 кЦ- "z J ⁿ

N nY b J 3    , шт/кг, (11)

c zn где c=bхnmin и a=bxnmax, n и b – постоянные коэффициенты.

Ниже приводятся вычисленные интегралы для некоторых значений “ n ”:

6          1 ^{- a} - c^c

N ₂ = — b ² - — + ^l--Ei ( - a ) + Ei ( - c )

ⁿ = - nY L a c

, шт/кг

Так как первый и третий члены в квадратных скобках малы, по сравнению со вторым и четвертым, то, пренебрегая ими, получим:

N 3 = — b1 l— + Ei(-c) n=2 nY L c

шт/кг

В дальнейшем, пренебрегая малыми членами, получим формулы для определения количества частиц, находящихся в единице массы (1кг):

3 b ³

N n = 1

πγ

l- c

c

V c

^

^{- 1 -} El ^{( - c} )

J

N

n =—

2 b ⁴ J l ^{- c} 1

nY I c 2

12 b ²

r-<

r-i

N n =2 =^ πλ

^- c

— I — 1 I- Ei ( - c ) c V c J

- c -—a

--Пт Гф ( V a ) -ф ( 4c ) 1[ . шт/кг

V c aa L \              / JJ

Для промежуточных значений n вычисление интеграла (1) можно выполнить приближенными методами.

Определение удельной поверхности сыпучего материала

Под удельной поверхностью песка или гравия понимают сумму поверхностей всех частиц, находящихся в единице массы S м2/кг, S см2/г и т.д. При теоретическом определении удельной поверхности предполагается, что форма частиц шарообразная. Конечно, частицы естественного материала далеки от шаровой формы, но точная оценка действительной формы частиц вряд ли возможна. Поэтому в результате подсчетов получается некоторая условная поверхность, меньшая, чем действительная, так как форма шара является идеальной геометрической формой, имеющей максимальный объем при минимальной поверхности.

Поэтому S_{действ.}=KS, где К>1 и этот коэффициент должен быть определен экспериментально:

Пусть V_x – объем одной частицы в мм³;

Sx – боковая поверхность частицы в мм3;

Y - плотность частицы в кг/м³;

nx – количество одинаковых по размеру частиц в 1 кг.

В единице массы материала находится ух долей по массе частиц, имеющих одинаковый размер. Масса этих одинаковых частиц будет равна:

Ух = VxY”x ,            (17)

откуда (учитывая размерность) получим:

nx

y 10 ⁹ x

.

Vxγ

Общая поверхность одинаковых частиц составляет:

nxSx

yx109 Sx ---------------------- .----------

.

γ

Для сферической частицы:

S   πx26

x

V   πx3

x

где x – диаметр частицы. Общая удельная поверхность частиц в 1 кг материала, выраженная в м2, будет равна:

x2 6 •Ю3 y

5= /——tdx ’м2/кг-x1 γ

Полагая y = l

1 — J

^bx ” • nbx” ¹ получим:

5 = 61103 [ l

γ x2

—J

■ bx”      i ” — 1 J

• nbx d , м 2 /кг_

Сделаем подстановку:

bxⁿ тогда

= z ,

Zn

Zⁿ 1      ¹

x = —p, dx —j— • z” 1 dZ, bn

x ” ^{— 1}

bnn i—2 zn ^—2 ' bn

Новые пределы интегрирования будут: при x=x1, Z=bxn1=c.

при x=x2, Z=bxn2=a.

Подставляя эти значения в выражение (22), получим:

5 =

6 • IO ³

γ

¹ a I" z

• b” j—• dZ ,м2/кг c Zn

Интеграл (25) может быть выражен через изученные функции только для некоторых частных значений показателей n . При других значениях n вычисление этого интеграла может быть выполнено известными приближенными методами. Если n=1, то интеграл выражается через интегральную показательную функцию:

c 6•io3 z

5 =-- b ” —:-• dZ ,   ₂

¹          м²/кг. (26)

γ _cZn

Для функции Ei ( — u ) Ei ( — u ):

Ei ( — u ) = 0,5772 + ln/ u / — — + u— + — + ...

1,1 2,2 3,3

Здесь С=0,5772 – постоянная Эйлера.

Если n=2, то интеграл приводится к фун- кции Крампа (интеграл вероятности):

a i-z jT c z

= П ф(4a )-ф(4c) . (27)

При n>1 в формуле (25) расширим пределы интегрирования, с=0 и а= * .

В этом случае интеграл приводится к функциям Гамма:

ГО 7-z              го jlr 'dZ-Jl-

0 Z n        0

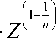
• dZ = Г

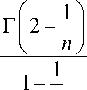
Из формулы (28) следует, что при n=1 удельная поверхность S= ~ . Это следует из того обстоятельства, что пределы интегриро-

вания выбраны 0 и ^ .

В этом случае необходимо пользоваться формулой (26).