Математический подход при установлении скорости распространения радиосигнала

Определение фазовой скорости электромагнитных волн в вакууме как

c = /

V еоЦо производилось без учета движения их источника и приемника [1–3]. Однако оно может быть учтено.

Целью настоящей работы является вычисление скорости распространения волнового электромагнитного импульса на основе исключительно математического подхода [4–8].

Актуальность, научная значимость . Правильный расчет скорости распространения волнового электромагнитного импульса позволит, в частности, корректно определять время прохождения радиосигналов на большие расстояния.

Определение скорости волнового электромагнитного импульса

Пусть источник И с часами неподвижно установлен в координате x ₀ = 0 связанной с ним системы координат (см. рис.) [9]. В момент времени t 0 он излучает волновой электромагнитный импульс.

К источнику со скоростью v приближается приемник П.

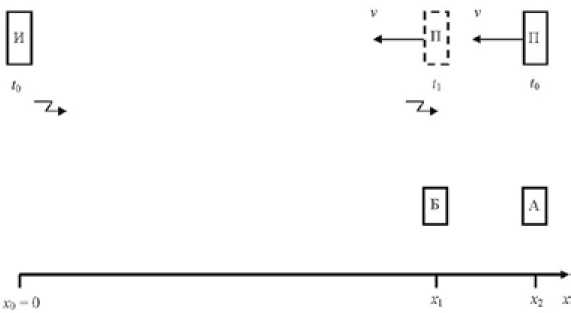
Рис. Расположение источника и приемника

Fig. Disposition of the source and the receiver

Устройство А с часами, синхронизированными с часами источника, установлено неподвижно относительно источника в координате x 2 . Оно регистрирует прохождение приемника через эту координату в момент времени t ₀.

Устройство Б с часами, синхронизированными с часами источника, установлено неподвижно относительно источника в координате x ₁. Оно регистрирует прохождение и приемника, и импульса через эту координату в момент времени t 1 .

По данным неподвижных наблюдателей, скаляр скорости приемника x2 - x v = —1

t i t 0

скаляр скорости волнового электромагнитного импульса относительно источника x1x0

c =------= t1 - 10     t1 - 10

По их же данным, скорость перемещения импульса относительно приемника определяется как отношение расстояния между ними x 2 - xо = x2

ко времени t1 - t0, за которое они это расстояние преодолеют, т.е. сблизятся c. = x2 = x2 - xi + xi = x2 - xi + xi = v + c ti -10 ti -10 ti -10 ti -10            .

Учет релятивистских эффектов

По мнению наблюдателя, движущегося вместе с приемником, система отсчета, связанная с приемником, непо

• v . К приемнику при

X₂Ji - v 2 .                                                                      (3)

c ²

Этот импульс

( t i - 1 0 )f"l

(величины x2, t1 и t0 движущийся наблюдатель может получить по радио от неподвижных наблюдателей и учес блюдателя, импуль

* c

x 2 7i - v 7 c²

⁽ t i ^- t 0 ⁾V^{i - v2}/c²

= v + c .

К этому же результату движущийся наблюдатель придет и без учета релятивистских по- правок.

Источник движется, приемник неподвижен

В системе координат, связанной с источником, источник неподвижен, а приемник приближается к нему со скоростью v . В этой системе координат выполняется соотношение (2). При переходе к системе координат, связанной с приемником, в том числе с учетом (3) и (4), реализуется выражение (5).

Заключение

Практической иллюстрацией полученного результата является разница во времени прохождения радиосиг рия при максималь

A t = S m

c - v c + v

= 2,17 - 10 8 ^{f 11}

® 0,273( c ).

,       ( 300000 - 56,6 300000 + 56,6

Здесь S_m – максимальное расстояние между Землей и Меркурием (км); c – скорость света в вакууме (км/с), v э – тангенциальная скорость орбитального вращения Меркурия (км/с).

Таким образом, скорость электромагнитных волн в вакууме складывается из (1) и разности скоростей источника и приемника.