Математическое и численное моделирование течений вязкого теплопроводного газа

Система нестационарных одномерных уравнений Навье - Стокса для вязкого теплопроводного газа включает три дифференциальных уравнения в частных производных, вытекающих из законов сохранения массы, количества движения и внутренней энергии газа. Предложенная в работе замена искомых функций в уравнениях неразрывности и внутренней энергии переводит закон сохранения массы и полной энергии из нормы пространства L ₁ в норму гильбертова пространства L ₂ . Впоследствии это значительно упрощает обоснование устойчивости и сходимости [1]. Дискретизация по пространству модифицированных уравнений Навье - Стокса осуществляется методом конечных элементов.

Для аппроксимации полной производной по времени каждого уравнения системы используется метод траекторий, который заключается в аппроксимации субстанциональной производной с помощью разностной производной назад по времени вдоль траектории движения частицы. Метод траекторий впервые появился в работах французских и американских ученых для аппроксимации уравнений Навье - Стокса для вязкой несжимаемой жидкости с первым порядком аппроксимации. Наибольшее теоретическое и практическое развитие метод получил для одного уравнения переноса массы [2]. Для решения систем алгебраических уравнений используется многосеточный метод с внешними итерациями по нелинейности.

Модификация уравнений Навье - Стокса обеспечивает повышение точности приближенного решения. Как следует из тестовых расчетов, абсолютная погрешность приближенного решения уменьшается в разы по сравнению с аналогичной погрешностью для немодифицированных уравнений, при этом разностная схема остается первого порядка. Применение комбинации метода траекторий и метода конечных элементов позволяет построить экономичный алгоритм с вычислительной точки зрения.

Математическая модель. Выпишем дифференциальные уравнения одномерного вязкого теплопроводного газа в виде безразмерных уравнений неразрывности, количества движения и уравнения для внутренней энергии:

d р   д u — + р— = 0, dt    дx (1) du   дP дт„ р— =--+ —, dt    дx   дx (2) de „uu   ,.   д qx р — + P— = Qt -   + Ф, dt    дx       дx (3) P = P(р, e), ц = ц(р, e), (4) где р - плотность; и - проекция вектора скорости на ось x; P - давление; ц - динамический коэффициент вязкости; e – внутренняя энергия; Q – внешний поток тепла от внешних источников; тензор напряжений тxx, проекция теплового потока qx и диссипативная функция Ф выражаются следующим образом:

4 1 д и            у    д e

=--ц—, qx =--ц—,

3 Re д x        PrRe д x

4 1 (ди ) 2 Ф =--ц — ,

3 Re I д x )

где Re – число Рейнольдса, Pr – число Прандтля, Y = 1,4.

Редукция уравнений. Преобразуем уравнения (1) и (3) к новому виду. Для этого, учитывая неотрицательность плотности и внутренней энергии, введем следующие функции:

P = G2,                         (6)

e = e ² .                              (7)

Подставим (6) в уравнение неразрывности (1) и получим

d ( g ²)    ₂ д и

——- + g²— = 0 .

dt       д x

Дифференцируя по t , имеем

, d g   ₂ д u _A

2 g—+ g ²— = 0 . dt      д x

Далее, сокращая последнее уравнение на 2g , полу чим d g 1 д u --+ —g— dt 2 дx

= 0 .

Проделаем аналогичную процедуру для уравнения внутренней энергии (3), т. е. преобразуем уравнение (3) к новому виду с учетом (7). Для этого подставим выражение (7) в (3), в результате получим

р d-^ +3 x=& - p d u ₊ф dt    d x    d t     d x

Преобразуем (10) следующим образом:

„ d£ dq   dQ ndu p2e— + —= —- P— + Ф. dt   dx    dt dx

Далее сократим последнее уравнение на 2 e и полу-

чим

Замыкают систему уравнений (16) - (18) алгебраические соотношения для давления и динамического коэффициента вязкости совершенного газа

P = P ( c,e ) , p = p ( c,e ) .               (19)

Дискретизация. В качестве расчетной области возьмем единичный отрезок Q = [0 , 1] с границей Г, состоящей из концов отрезка. Введем равномерную сетку x_t = th , i = 0 , 1 ,..., n с шагом h = 1 / n ( n >  2).

Обозначим множество узлов области Q :

Q _h = { S = ( x ) , i = 0 , 1 , •••, n } ,

1 d q x = X d Q - P d u ₊ X Ф. dt  2 e d x   2 e d t 2 e d x 2 e

введем множество внутренних узлов

Q h = { S , = ( x ) , t = 1 ,..., n - 1}

Подставим (7) в выражение для теплового потока q_x из (5) и возьмем производную по х , получим

и два граничных узла

Г h = { S t = ( x ) , t = 0 , n } .

qx

2 y de ----pe—, PrRe d x

^d q x d x

2 y    fdel d f del

---- p| — I +e — I p— I

PrRe X x)   d x ( d x)

V                          zy

В результате расчетная область Q разбилась на n интервалов.

Для каждого узла S _t е Q _h введем базисную функцию ф , - ( x ):

С учетом (13) и выражения для диссипативной функции Ф из (5) уравнение (12) примет вид

Ф / ⁽ x ) =

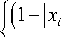
^- x ) ,

^ 0,

d £    у p f de )    d f de 1

p , „ „ H^I +^i p^I dt PrRe e ^d x ) d x ^ d x )

1 P d u   2 pX u 1 ²

= —Q t ---+——I   I .

2 e     2 e d x 3Re e X x J

x е [x-1, x+1], x е (x-1, x+1),

которая равна единице в S и равна нулю во всех ос тальных узлах Q .

Будем искать приближенное решение в виде

Замечание. Обратим внимание на появившиеся множители p/e и P /e в уравнении (14), которые,

как показывают расчеты, являются естественными «регуляризаторами». Например, для совершенного газа уравнение состояния (4) запишется как

P = P ( Y- 1) e или P = Х( у- 1) e ² . (15)

Поскольку внутренняя энергия всегда положительна и больше единицы по отношению к ее величине на бесконечности, то множитель 1 / e «гасит» растущее как e ² давление. Аналогичны рассуждения относительно p/e . Для совершенного газа, как сле-

n оh (t, x) = ^Х t )ф,(x),

/ =0

n uh (t, x) = ^ u (t )ф/ (x),

=0

n e h(t, x) = Se/(t )Ф,( x).

=0

После дискретизации по пространству уравнения (16) получаем дискретный аналог уравнения неразрывности:

дует из формулы Сазерленда, динамический коэффициент вязкости является степенной функцией от внутренней энергии.

Будем решать систему уравнений, преобразован-

^{d CT} l , 1 - /              . л

——+—xi(ui+1- ui -1) = 0, dt   4h l = 1,..., n -1.

ную к следующему виду:

d ст

--+ -G= dt2

du

p—= dt

5 P , dr xx d x   d x ’

d e     у p f de 1    d f de 1

p , -Ы +^lu^i dt PrRe eXx )  dx ^ dx )

1 P d u   2 pX u 1 ²

= —Q t ---+——I I .

2 e     2 e d x 3Re e X x )

Дискретный аналог уравнения количества движения (17) принимает следующий вид:

du_l    2 1

pI+         ((ui - ui-1)(pI-1 + pI)- dt 3h2 Re

- ( u i +1 - u i )( p i +p i +1 )) =                (25)

= X7^{( P} _i -1 ^{- P} _{i + 1}) ,     ⁱ = 1 >-"> ^{n -} 1 .

По аналогии с предыдущим уравнением выпишем дискретный аналог уравнения энергии (18) в следующем виде:

d si    1 Y P и

Р i-7 -777 ™--((s i+i dt   2 h2 PrRe s i

^-s i ^{) 2} + ^{( s} i -^s i -i ^{) 2 )} +

_k+i/„x _k+i   . k +i/„x . k +i „ k++i/..\ k++i o (Xi) — oi , u (Xi) — ui    и s (Xi) — si вы-

• 1    Y

  ⁺ 777 7777" ^{(( s} i - ^s i -i ^{)( ц} i -i ^{+ Ц} i ) - ^{( s} i +i - ^s i ^{)( ц} i ^{+ Ц} i +i )) = 2 h ² PrRe

• ¹    P /              x 1 ^{1 Ц} I               X2 . /             2

  -——⁽ u i +i - u i -i ) ⁺— ⁽⁽ u i +1 - u i ) + ⁽ u i - u i -i ) ) ,

4 h sj              3 h ² Re s _i

I — i ,..., n - 1 .                       (26)

пишем каждую систему.

Для уравнения переноса массы система алгебраических уравнений относительно неизвестных o ^{k + i}

имеет вид

I h . ⁱ / k k x | k +i _ h k / x

I ^{— +} T⁽ u i +i ^- u i -i ) l ^o I = ^{— o ( X} I ) , 1т 4             ) т

Метод траекторий. Введем равномерную сетку по времени с шагом т — t fin / m :

i — i ,..., n - 1 .

® т = {t k : t k — k т,       k — 0 ,..., m } .

Для уравнения количества движения система алгебраических уравнений относительно неизвестных в k +1

узлах разбиения u имеет вид

Производную по времени (субстанциональная) в уравнении (24) аппроксимируем с помощью разностной производной назад по времени вдоль траектории движения частицы следующим образом [2]:

d G , О ^{k + i} ( x_l ) -o ^k ( X k ) ---®-------------- dt             т

где X k - решение при t * = k т уравнения

— = u ( t *, X ) ,    X (( k + 1) т ) = x .        (28)

dt

Для численного решения уравнения (28) применим метод Эйлера, вычисление производится с ( k + 1)-го шага назад по времени. Полагая, что частица в промежутке времени ( t k , t k ₊₁) движется равномерно, получаем

X k — x_i - u ( t * , x_i ) т.                (29)

Обозначим u ( t * , x_i ) = u k . Значение o ^k ( X k ) определяется путем линейной интерполяции.

При u k >  0

k / x k / x । / x^ k      x ^{o ( x} i ) ^{o ( x} i -1 ) 22

^{o (} X i ) ^{— o (} xl ) ^{+ (} XI ^- x i )------------------ . ⁽³⁰⁾

x i ^- x i - 1

При u k <  0

k / x k / x . / у к      x o (xi +i) o (xi ) /2 1 X o (Xi ) — o (xi ) + (Xi - xl )------------------. (3i)

x i + i ^- x i

Производную по времени в уравнениях (25) и (26) аппроксимируем аналогично разностной производной (27), в результате получим

du i ~ k +i u ^{k + i} ( X i ) - u ^k ( X k )

¹ dt ⁱ               т

-

3 h ² Re

k +1      ^ i

P i ₊ ^{2 1} т    3 h ² Re

+

-

. k . ,,k\ „ k +1 .

^{( ц} 1 - 1 ⁺ P i ) ui -i ⁺

^{( ц} k -i^{+ 2 ц} k ^+ц k +i ) u k ^{+ i +}

J (35)

2    1 , T T . T+1

2 то ^{(Ц +P} i +i) u i +1 ^—

3 h ² Re J

k +i                   ,

—       u ^k ( X i^k ) + — ( P ^k i - P ^k +i ) ,      i — 1 ,..., n - 1 .

т             2 h

Система квазилинейных алгебраических уравнений, соответствующая уравнению внутренней энергии, выглядит следующим образом:

k

^- kv^k

„ , 2             к ^(s i ^s i -i )

2 h ² PrRe s k

1 Y

-

^Y ( p k i + P ^k ) s ^k V i •                        i

2 h ² PrRe

+

+

k +1 P i

т

+

Y Ц k

2 h ² PrRe s k

1 Y

2 h ² PrRe

kk k

^{(2 s} i ^-s i +i ^-s i -i ) ⁺

(2 ц k +ц k +i +ц k -i ) s k ^{+ i} +      (36)

A—4 (s k ₊i -s k ) - A— ( ц k +ц k₊ d]e k ₊⁺i — 2 h ² PrRe s k            2 h ² PrRe

n k +1

—^s k ( X k ) -

т

₊      P k

3 h ² Re s k

^{1 P} i k _v k +1 ,,k +ix .

—Г ^{( u} +1 ^{- u}i -i ) ⁺

^{4 h} s k

k +1     , k +ix2 , / k +1     , k +ix2i

^[( u i +1     u i ) ^{+ (} u i       u i -i ) ^] ,

i — 1 ,..., n - 1 .

d s i k +i s k ^{+ i} ( x i ) -s ^k ( X k )

^{Р i} lT "^{p 1}         т

Значения u ^k ( X k ) и s ^k ( X k ) вычисляются путем линейной интерполяции, аналогично o ^k ( X k ).

Системы алгебраических уравнений. После аппроксимации производной по времени в дискретных аналогах (24) - (26) получаем системы квазилинейных алгебраических уравнений. С учетом обозначений

Таким образом, получена консервативная вариационно-разностная схема первого порядка аппроксимации.

Для решения систем линейных алгебраических уравнений с трехдиагональной матрицей используется метод немонотонной прогонки, который отличается высокой вычислительной устойчивостью [3].

Тестовые расчеты. Для тестирования полученной математической модели функции u , o, s задаются следующим явным образом:

u ( x , t ) — x ( x - 1) ² 1 ,

g ( x , t ) = x ( x - 1) 2 t + 1 ,               (37)

e ( x , t ) = x ( x - 1) 2 t + 1 .

При подстановке функций (37) в исходные уравнения и модифицированные уравнения получаются соответственно правые части f , , f _? , f u , f e и f . , которые учитываются в системах уравнений при их численном решении. Нормы погрешности в пространстве L 2 и L _L определяются следующим образом:

II S a L = №> a ) 2 dx 1 ²

sa = a;- a* |,

Lsa)2dx = |[|a0— a0A| + a;-ahA J + hEL*-a,| , 2 ^                                1

ii^{s a} l, , = max k- ^a,\ •

Для ||ба||да, и ||5р||ю, можно получить соотноше- ние

II N™ ,, =IML ,, max Iе

Норму ||Sp| |₂ , можно выразить через ||Sc i ||_ю , следующим образом:

f h                                      n-1) 2

II ^Sp| L, h = kl^PlI " , h ⁺II^SP n il », h ■ ^h EI^P i ll », h ,

12                                      i=1

II5pIL,h = [I Ol5^olL.h |°0+°0|) +(ll5°nlL,h |аП+°П|)]+ n-1 1^2 ) 2

^{+ h} E (ll⁵ ° i L, h ^{a ; +a h} l 1 • i =1 ^j

Нормы погрешностей в табл. 1 и 2 приведены для шага по времени т = 0,000 1 в момент времени t = к т ( к = 1000).

Задача о распространении теплового импульса. При решении модельной задачи тепловой импульс задается в окрестности центра расчетной области, газодинамическая постоянная у , число Рейнольдса Re, число Прандтля Pr, число Маха M _L и ю имеют следующие значения: у = 1,4, Re = 2 - 10 ³ , Pr = 0,7 , M „ = 4 , ю = 0,8 [4 - 6]. Температура T определяется из следующего уравнения состояния: