Математическое и физическое моделирование самоустанавливающихся замков для сборки и раскрытия составных твердотельных космических зеркал

«Московский физико-технический институт (государственный университет)», 2018

и высокую повторяемость установки оптических элементов - линз, зеркал, призм, фотопластинок - на оптической скамье. Позднее этот метод объединения элементов конструкции получил в англоязычной литературе название kinematic couplings (см., например, в Википедии . Приспособления модернизировались, дорабатывались и использовались для решения различных научных и прикладных задач. Последние десятилетия эти устройства нашли применение в нанотехнологиях. Здесь при высококачественном изготовлении элементов приспособления удается обеспечить микронный и субмикронный уровень точности и повторяемости сборки элементов конструкции [2-6].

Цель статьи - показать, что эти конструкции лабораторной оптики (при некоторой естественной модификации) оказываются полезными для задач конструирования составных зеркал больших космических телескопов. Такая неочевидная связь классической оптики и механики космических конструкций кажется нам достойной обсуждения и изучения.

Мы будем называть данные соединения кинематическими связками и исследуем возможность создания на их основе механических самоустанавливающихся замков для космических приложений. Замки могут найти применение, например, для решения задач сборки или автоматического раскрытия больших составных зеркальных антенн [7-10]. (см. также электронные ресурсы ,, http: // .

Основу кинематической связки в версии Максвелла составляют три V-образных паза (рис. 1а), размещаемых на одном из соединяемых элементов (основании), и три шаровых опоры, связанные с треногой - вторым соединяемым элементом (рис. 1в). В рабочем состоянии шаровые опоры находятся на дне пазов и удерживаются в этом положении силой тяжести (рис. 1с, d).

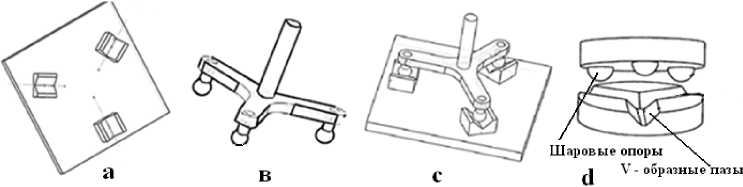
Рис. 1. Кинематическая связка: а. - V-образные пазы на несущем основании, в - три шаровых опоры, связанные с треногой, с - кинематическая связка, в сборе, d - современная кинематическая связка, оптического качества.

Три особенности приспособления обеспечивают ему важные механические свойства.

Во-первых, рабочее положение устройства является равновесным состоянием конструкции. При малых смещениях треноги возникает усилие, возвращающее устройство в равновесное рабочее состояние.

Во-вторых, состояние равновесия единственно, что обеспечивает высокую повторяемость установки треноги на. основание.

Наконец, в-третьих, в равновесном состоянии конструкция оказывается статически определимой, что гарантирует ненапряженную сборку приспособления. Действительно, каждая шаровая опора, удерживаемая на. дне V-образного паза, вносит в конструкцию два. кинематических ограничения. В невырожденном случае общее число кинематических ограничений в конструкции равно шести, что гарантирует ее статическую определимость. Невырожденность системы достигается выбором направлений V-образных пазов.

С точки зрения механических свойств связок естественно различать следующие случаи. Связка, может находиться в равновесном состоянии и в состоянии, смещенном относительно состояния равновесия (неравновесная связка). Если равновесное состояние единственно, то конструкция геометрически неизменяемая. Изменяемые связки могут быть мгновенно изменяемыми, т.е. допускающими бесконечно малые смещения относительно состояния равновесия, но могут допускатв изменения не малой, а конечной величины. В последнем случае связка превращается в механизм.

С прикладной точки зрения наибольший интерес представляют неизменяемые связки, поскольку в этом случае связка обладает самоустанавливающимся свойством, т.е. самопроизвольно возвращается в положение равновесия, которое и является желательным при ее применении. Именно это свойство использовали Кельвин и Максвелл при конструировании и последующей юстировке оптических систем.

• 2.    2В-кинематические связки для работы в условиях невесомости

• 2.1.    Физическая модель 2В-связки

• 2.2.    Математическая модель равновесного состояния 2В-связки

Исследование кинематических связок естественно начать с того случая, когда все V-образные пазы лежат в одной плоскости. Мы будем называть такие связки двумерными (2В-связками).

Для того чтобы использовать идею классической кинематической связки для сборки составных космических конструкций, необходимо преодолеть две трудности.

Во-первых, необходимо предложить способ удержания шаровых опор на дне У-образных пазов в условиях невесомости. В классической связке опоры удерживаются на дне пазов силой тяжести. В новых условиях нужно сохранить кинематику связей и направление удерживающих усилий в равновесном состоянии. С этой целью была предложена конструкция и изготовлена физическая модель пружинного захвата, представленного на рис. 2а. Здесь, с одной стороны, сохранены четыре степени свободы во взаимном перемещении соединяемых элементов, с другой - удерживающее усилие направлено по нормали к основанию паза. На рис. 2в представлена физическая модель 2В-кинематической связки с пружинными захватами для работы в условиях невесомости в сборе. Мы использовали физическую модель пружинного захвата, предложенную и изготовленную А.Ю. Тондриком (ФИАН).

Рис. 2. Физическая модель 2В-кинематической связки: а. - пружинный заахват сферической опоры, в - кинематическая связка, с пружинными захватами в сборе

Во-вторых, необходимо выяснить, при каких взаимных положениях пазов конструкция сохраняет самоустанавливающиеся свойства. В классической кинематической связке, использующей схему Максвелла, V-образные пазы расположены на. плоскости симметрично относительно центра, связки. Наша, цель - соединить между собой твердотельные зеркала. с помощью кинематических связок, сохранив свойство повторяемости сборки. При произвольной форме соединяемых зеркал сохранить классическое положение У-образных пазов кинематической связке не удается, пазы и шаровые опоры приходится размещать по боковым сторонам соединяемых элементов на. значительном расстоянии друг от друга. Возникает вопрос: при каком взаимном положении пазов сохраняются самоустанавливаю-щиеся свойства, конструкции? Для ответа, на. этот вопрос построим математическую модель, описывающую работу ЙВ-связка при произвольном располоэюении V-образных пазов.

Рассмотрим на плоскости OX1 X2 три отрезка ш ¹ ,ш² , ш³, взаимное положение которых совпадает с взаимным положением оснований V-образных пазов 2П-связки (рис. За). Назовем эти отрезки направляющими. Треугольник а¹ а² а³ моделирует положение треноги связки, его вершины в равновесном состоянии удерживаются механическими связями на направляющих.

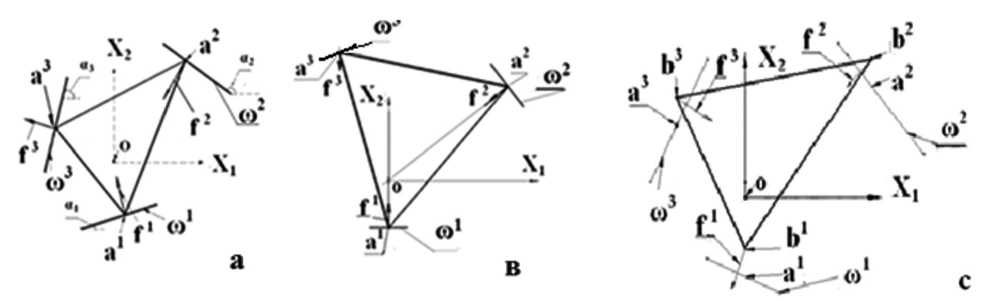
Рис. 3. Равновесные (а, в)

и неравновесное (с) положения 2Р-кинематических связок

Пусть аг - угол между направляющей шг и осью OX1, пг - вектор нормали к шг , /г - вектор реакции связей (направлен по нормали к шг) , /г - численное значение реакции связей. Тогда fг _ (-Һ sin аг А _ г

;       /г COS аг)    /г П, пг = (— Sin агА , (г = 1, 2, 3).

у cos а_г J

Условия равновесия - сумма проекций сил на оси OX₁ , OX2 и сумма моментов сил относительно начала координат - имеют вид

-/1 sin ai - /2 sin а2 - /3 sin аз = F1 ,

/1 cos ai + /2 cos а2 + /3 cos аз = F2                          (1)

[а¹ /¹ ] + [а² / ² ] + [а³ /³ ] = /1 [а¹ п¹ ] + /2 [а² п² ] + /3 [а³ п³ ] = М.

Здесь векторные произведения [а¹ /¹ ], [а²/²], [а³/³] определяют моменты сил реакций связей /¹, /², /³ относительно начала координат, F₁ и F₂ - проекции суммы внешних сил на оси OX₁, OX₂ соответственно, М - сумма моментов внешних сил относительно начала координат.

Перепишем систему (1) в матричном виде

А • / = F,

где

( — sina₁ cosa₁ [а¹ п¹ ]

— sina2 — sina3\      //Д      /F1

cos а2    cos а3   , / = /2  , F = F2

[а2 п2 ]     [а3 п3 ]             /3            F3

Здесь А - матрица равновесия. Система (2) не вырождена - геометрически неизменяема, т.е. имеет единственное решение, если определитель матрицы равновесия А отличен от нуля. В невырожденном случае связка обладает самоустанавливающимися свойствами. Для выяснения условий вырождения конструкции введем систему координат, в которой ось OX1 параллельна ш1, а начало координат совпадает с точкой пересечения нормалей к ш1 и ш2 в точках а1 и а2 (рис. За). В новой системе координат матрица А принимает вид

А =

/ 0

— sin a2 cos a2 0

— sin a3

cos a3 [а3 п3 ]

Отсюда находим det А = sin «2 [а3п3].

sin «2 = 0 и [а3п3] = 0,

Поэтому если то конструкция геометрически неизменяема, состояние равновесия единственное и кинематическая связка действительно обладает самоустанавливающимися свойствами.

• 2.3.    Вырожденные конструкции

Перейдем теперь к вырожденным конструкциям, которые являются по крайней мере мгновенно изменяемыми. Рассмотрим возможные случаи вырождения. На практике проверку невырожденности удобно проводить, убеждаясь, что исследуемая система не принадлежит ни одному из указанных ниже типов.

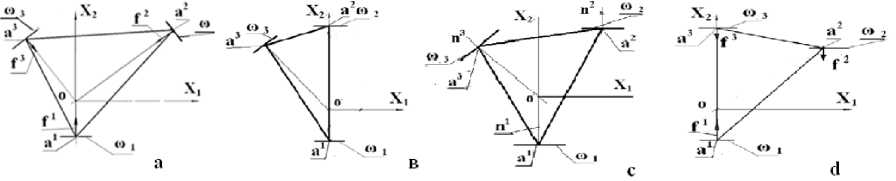
Рис. 4. Вырожденные состояния связки: а. - вырожденное состояние 1, в - вырожденное состояние 2.1, с - вырожденное состояние 2.2, d - вырожденное состояние 3 (конструкция превращается в механизм)

А =

— sin «1 cos «1 [а1п1]

— sin «2 cos «2 [а2п2]

— sin «з cos «3 [а3п3]

\ 0 [а2п2]

— sin «3 cos «3 0

Отсюда находим det А = — sin «3 [а2п2].

Конструкция геометрически неизменяема.

• 3.    Линии ш1,ш²,ш³ паралельны (рис. 4d). Матрица А системы (1) принимает вид

  ( — sin «1 cos «1 [а¹ п¹]

  
  

  — sin «2 cos «2 [а²п²]

  
  

  — sin «3 cos «3 [а³п³]

  
  

  [а¹ п¹ ]

  
  

  [а²п²]

  
  

  13     .

  [а³ п³ ]

  
  

Отсюда det А = 0.

Конструкция вырождена - возможно движение треугольника вдоль направляющих.

Проиллюстрируем использование рассмотренных представлений на конкретном примере.

В классических работах Максвелла V-образные пазы находятся в одной плоскости симметрично относительно центра связки. Во многих случаях необходимо отказаться от такого симметричного размещения элементов конструкции, не теряя самоустанавливающегося свойства. На рис. 5 представлена физическая модель двух твердотельных поверхностей, объединенных кинематической связкой с разнесенными V-образными пазами. Конструкция оснащена пружинными захватами шаровых опор. Непосредственно вычисляя определитель матрицы равновесия, убеждаемся, что при выбранном положении V-образных пазов он отличен от нуля. Это же обнаруживается и в физическом эксперименте - конструкция является жесткой. Итак, предлагаемая конструкция геометрически неизменяема и обладает высокой повторяемостью сборки.

Рис. 5. Две пластины, объединенные кинематической связкой с пружинными захватами

• 2.4.    Математическая модель неравновесного состояния связки и оптимизация жесткости

Из построенной математической модели следует, что при произвольном размещении V-образных пазов конструкция, как правило, обладает самоустанавливающимися свойствами. Поэтому в классе самоустанавливающихся связок можно сформулировать задачу оптимизации тех или иных характеристик соединения. Мы рассмотрим задачу оптимизации одного из элементов матрицы жесткости составного зеркала - крутильной жесткости связ ки.

Для этого построим матрицу жесткости и найдем выражение крутильной жесткости 2Е)-связки как функцию углов «1, «2, «3 - направлений V-образных пазов.

Элементы конструкции - треногу, основание и V-образные пазы - будем считать твердыми телами. При «деформации» конструкции - смещении треноги из равновесного состо яния - возникают возвращающие усилия, величины которых определяются пружинными захватами шаровых опор. Возвращающие усилия приложены к вершинам треугольника и направлены по нормалям к направляющим w1,w2,w3. Величины усилий пропорциональны расстояниям от вершины до соответствующей линии ш1,ш2,ш3.

На рис. Зв, с показаны схемы равновесного и неравновесного положения связки. Построим матрицу жесткости G системы, связывающую обобщенный вектор внешних усилий (сил и моментов) с обобщенным вектором перемещений треугольника (смещений и поворотов):

Ғ = G • d, ( 3)

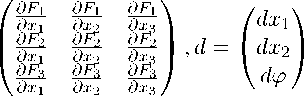
^Ғ1               91,1   91,2   91,з

^Ғ = I ^Ғ2 I ^,G = I 92,1  92,2  92,3

^ғз             9з,1   9з,2  9з,з

Наряду с уравнениями равновесия (1) рассмотрим 2П-связки:

систему совместности деформаций

В • d = 8, где

(— sin «1  cos «1  [a1n1]\       /dxA/d1A

• —    sin «2  cos «2  [a2n2]   , d =   dx2   , s =   dl2,

• —    sin «2  cos «2  [a2n2]/       \d^/\dla/

Вектор d определяет малые смещения треугольника (перемещения по координатным осям и поворот), вектор определяет расстояния от смещенных вершин треугольника до направляющих. Важно отметить, что

В = Ат.(5)

Считая все пружинные захваты одинаковыми, запишем закон Гука:

/ = к • s,(6)

где к - коэффицент упругости. Подставляя (6) в (1), имеем к • А • s = F.(7)

Далее, подставляя (4) в (7), получаем к • А • В • d = F.(8)

Сравнивая (3) и (8) и учитывая (4), находим выражение для матрицы жесткости связки:

91,1

91,2

92,2

93,2

91,3

92,3

93,3

G = к • А • В = к • А • Ат =92,1

93,1

= к •

— sin «1 cos «1 [a1n1]

— sin «2

cos «2 [a2 n2 ]

— sin «3 cos «3 [a3n3]

— sin «1 cos «1 [a1n1]

— sin «2 cos «2 [a2n2]

— sin «2 cos «2 [a2n2]

В качестве примера рассмотрим задачу оптимизации крутильной мсесткости 2В-связки.

Пусть из конструктивных соображений положения центров V-образных пазов определено - векторы a1, a2, a3 заданы. Требуется выбрать направления пазов (углы «1, «2, «а), при которых крутильная жесткость связки принимает наибольшее значение.

Крутильная жесткость задается элементом 93,3 матрицы жесткоети ( 3). Из (9) для 93,3 имеем

93,3 = 1^ = к • ([a¹ • n¹]² + [a² • n²]² + [a³ • n³]²).

Введем обозначения:

U («j) = [a¹ • n^j]² = (a1 • cos «1 + a2 • sin «1)2, i = 1, 2, 3.

Тогда в точках экстремума выполняются условия dU д«1

= 2 • (al • cos «1 + a2 • sin «1) • (—al • sin «1 + a2 • cos «1) = 0.

Отсюда возникают две возможности. Первая из них:

(a1 • cos «1 + a2 • sin «1) = 0

(Ю)

соответствует минимуму крутильной жесткости связки. В этом положении направляющая ортогональна линии (рис. ба), конструкция мгновенно изменяема.

Вторая возможность:

(—a^ • sin «1 + a2 • cos «1) = 0.

(И)

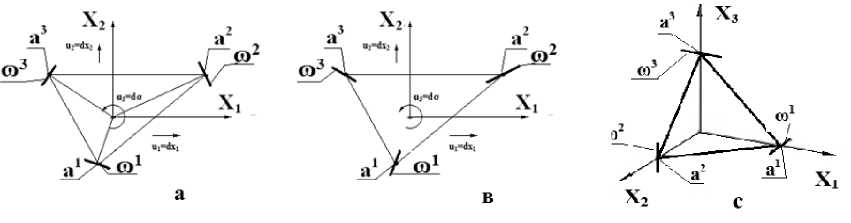
Рис. 6. Экстремальные состояния 2В-кинематической связки и пространственная кинематическая связка: а. - состояние минимальной крутильной жесткости 2В-связки, в - состояние максимальной крутильной жесткости 2В-связки, с - прострапствеппая кинематическая связка.

Вычислим вторую производную функции U («1):

-—2 = —2 • [(a1 • cos «1 + a2 • sin «1)2 + (—a1 • sin «1 + a2 • cos «1)2]. d«i

Если выполнено условие (10) и не выполнено условие (9), то d2U д«2

—2 • [(a1 • cos«1 + a2 • sin«1)2] < 0, т.е. положение соответствует максимуму крутильной жесткости связки (рис. бв), направления и совпадают.

• 3. ЗВ-кинематические связки

Откажемся теперь от условия двумерности связки. Это необходимо потому, что при соединении поверхностей сложной формы нереально требовать расположения всех пазов в одной плоскости. Классическая кинематическая связка, использующая V-образные пазы, предполагает размещение пазов на. плоском основании. Для соединения криволинейных зеркал необходимо разместить пазы в пространстве и гарантировать самоустанавливаю-щиеся свойства, конструкции. К сожалению, в общем трехмерном случае получить пригодные для практического использования аналоги условий, полученных выше для двумерных связок, пока не удается. Однако это удается сделать для ряда практически важных случаев.

Рассмотрим пространственнуто кинематическую связку, пазы которой расположены согласно рис. бс. Эта. связка, очевидно, не является двумерной, однако, как мы сейчас покажем, ее исследование можно провести с помощью рассмотренных выше методов исследования двумерных связок.

Покажем, что при таком пространственном расположении V-образных пазов конструкция геометрически неизменяема, и ЗП-связка. тоже обладает самоустанавливающимися свойствами. Положения точек a1, a2, a3 и направления V-образных пазов определяются векторами:

a ¹ = (al  0  0) , a ² = (0  a2  0) , a ³ = (0  0  a3) ,

и ш1 = (0  1  0) , ш2 = (0  0  1) ,ш3 = (1  0  0) .

Уравнения равновесия сил и моментов имеют вид

У 1 + У ² + У ³ = f,

[a1 • У 1] + [a2 • У2] + [a3 • J3] = М, где J 1, J2, У3 - реакции св язей в точках a1, a2, a3, FТ = (Ғ Ғ2 Ғ3) - вектор суммы внешних сил, МТ = (М1 М2 М3) - вектор суммы внешних моментов.

При выбранных а/а2.аз и ш1,ш2,шз для реакций связей имеем

₁        (︀ _{1               1} )︀       ₂        (︀ _{2        2}        )︀       ₃        (︀           _{3        3} )︀

J ^{— /}1   ^{0   /}з , ^/ — ^/1  И ⁰ ,^{/ — 0 /}2 J3 .

Здесв б неизвестных, которые нужно найти из условий равновесия. Три уравнения находим из условия равновесия сил:

/1 + /1 ² — Ғ1, /2 + /2з — Ғ2, /з + /з ^з — ғ₃.

Для вычисления моментов используем выражение

Тогда

г

[ а • / ] — ах

/1

3 а2 /2

к аз /з

а2

/2

аз /з

• •    г —

а1

/1

аз /з

• •    3 +

а1

/1

а2

/2

• к.

г

[ а ¹ • / 1 ] — а1

/11

к

0 /з

— 0 • г

-

а1 /11

/з ¹

• 3 +

а1 /11

• к —

^-а1 • ^/1 • 3,

[ а ² • /2 ] —

[ а ³ •/3 ] —

г

0 /2

3 а2 /22

к

— 0 • г

-

0 • 3 +

/2

а2 /2

• ^{к —} -а2 • /2 • ^к,

г

/2

к аз /з

/2

аз

/з ^з

• •    г —

⁰ • J ^{+ 0} • ^{к — —а}з • ^/з • г.

Условия равновесия моментов принимают вид

[а1 • /1] + [а2 • /2] + [аз • /з] — —аз • /з •г — а1 cot/з •3 - а2 • /2 • к — М, или в координатном виде:

• — аз • /2з — М1,(15)

• - а1 • /з1 — М2,(16)

• — а2 • /12 — Мз.(17)

Введем в рассмотрение вектор искомых неизвестных:

fт _(f1   f1   f2   f2   f3

/  — /1   /з  /1   /2  /2

вектор внешних воздействий:

Фт — (Ғ1 Ғ2 Ғз М1 М2 Мз) , и перепишем систему (12) - (17) в матричном виде:

В •/ — Ф ,

Z 1		0	1	0	0	0 ^	//1^		/Ғ1 \
	0	0	0	1	1	0		/з		Ғ2
В —	0 0	1 0	0 0	0 0	0 3 —аз	1 0	·	/2 /22	—	Ғз М1
	0	—а1	0	0	0	0		/з		М2
	0	0	—а2	0	0	0	\ /з з7		\ Мз/

Если det В — 0, то система невырождена, конструкция геометрически неизменяема, состояние равновесия единственное и система обладает самоустанавливающимися свойствами. Раскрывая определитель, находим

	1	0	1	0	0	0
	0	0	0	1	1	0		⃒1	0	0
det В — det	0 0	1 0	0 0	0 0	0 3 — a3	1 0	— —ai • a2 • аз •	0 ⃒⃒0	1 0	0 1	— —ai • a2 • аз
	0	—al	0	0	0	0
	0	0	—a2	0	0	0

Таким образом, если числа ai, а2 и а3 отличны от нуля, то связка, V-образные пазы которой расположены согласно рис. бс, обладает самоустанавливающимися свойствами.

Рассмотренное размещение пазов ЗИ-связки было использовано в физической модели, представленной на рис. 7. Здесь показаны два параболических лепестка, связанных само-устанавливливающимися замками на сборочном стапеле (рис. 7а), два лепестка в сборе (рис. 7в) и пружинные захваты шаровых опор (рис. 7с, d)).

Моделирование подтвердило геометрическую неизменяемость и простоту сборки составного зеркала.

Рис. 7. ЗВ-кинематическая связка, двух параболических лепестков: а. - сборка, двух лепестков па. шаблоне, вид сзади, в - два. лепестка, объединенные кинематической связкой, вид спереди, с -вертикальный захват шаровой опоры, d - горизонтальный захват шаровой опоры

• 4.    Кинематическая связка в задаче раскрытия составного зеркала

Замечательно, что методы кинематических связок для точной сборки составных зеркал можно, слегка, модифицировав, использовать и для другой родственной задачи - задачи о раскрытии составных зеркал. Эта. задача, особенно важна, при конструировании составных зеркал для орбитальных телескопов.

Мы исследовали классическую конструкцию трансформируемого лепесткового зеркала, выполненного по схеме корпорации Дорнье [10].

Конструкция включает в себя центральное зеркало и набор лепестков, каждый из которых связан с центральным зеркалом цилиндрическим шарниром. Раскрытие зеркала, осуществляется синхронным вращением лепестков вокруг осей шарниров (рис. 8). Было показано, и в этом заключается ключевая находка, разработчиков корпорации Дорнье, что существует такое направление осей цилиндрических шарниров, при котором переход лепестков из сложенного состояния в раскрытое осуществляется без зацепления лепестков.

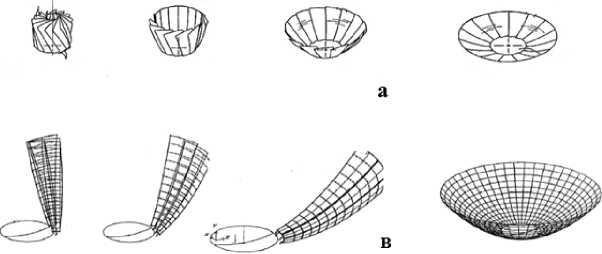
Рис. 8. Классическая схема, раскрытия лепесткового зеркала. В верхней части рисунка, показаны последовательные фазы раскрытия зеркала. В нижней части рисунка, показаны соответствующие изменения в положении отдельного лепестка, а. па. последнем изображении нижнего ряда. - раскрывшаяся конструкция в целом

Эта. конструкция была, использована, при создании антенны космического радиотелескопа проекта Радиоастрон [11] и эффективно работает в сантиметровой области спектра. Однако для работы зеркала, в миллиметровой и субмиллиметровой области спектра, достигаемой точности отражающей поверхности оказывается недостаточно.

Мы изучали возможность повышения с помощью кинематических связок точности и повторяемости раскрытия отдельного лепестка. [12-14]. С этой целью была, построена, физическая модель системы раскрытия лепестка и проведены ее исследования. В модели на обратной стороне лепестка у его основания размещались три шаровые опоры (рис. 9). На станине, имитирующей основание центрального зеркала, устанавливались три У-образных паза. Перевод лепестка, из сложенного (транспортного) положения в раскрытое (рабочее) состояние осуществлялся вращением лепестка вокруг оси, соединяющей лепесток с основанием центрального зеркала. На заключительном этапе раскрытия шаровые опоры фиксировались на дне V-образных пазов.

При моделировании выяснилась одна, важная и интересная особенность использования кинематических связок в задаче раскрытия. С одной стороны, для точной фиксации конечного состояния раскрываемой конструкции кинематическая связка, должна, быть статически определимой. С другой стороны, механизмы раскрытия вносят в систему дополнительные кинематические ограничения, и в момент попадания шаровых опор на. дно V-образных пазов конструкция становится неопределимой и связка теряет самоустанавли-вающиеся свойства.

Для решения этого противоречия в механизм раскрытия была, введена, система, с переменной структурой. Раскрытие осуществлялось в два. этапа. На начальном этапе низкоточного раскрытия модель лепестка, переводилась из транспортного состояния в состояние, близкое к рабочему, вращением лепестка, вокруг оси цилиндрического шарнира, согласно схеме Дорнье. На заключительном этапе точной фиксации рабочего состояния лепестка связь с центральным зеркалом отключалась, и удержание шаровых опор на дне пазов осуществлялось пружиной, которая создавала усилие, соответствующее требованиям кинематической связки. В лабораторных экспериментах была, достигнута. 10-микронная точность повторяемости раскрытия модели (имитатора) лепестка, (по нормали к отражающей поверхности), смещение в тангенциальной плоскости не превышало 30 микрон. Этапы физического моделирования представлены на рис. 10.

При проведении физического моделирования мы заменяли (не изменяя сути конструкции) лепесток более простым элементом, который ниже упоминается как имитатор лепестка.

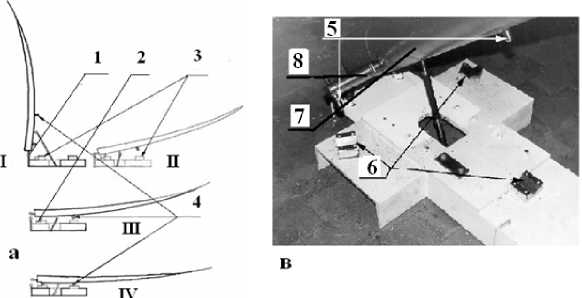
Рис. 9. Кинематическая связка, в системе раскрытия лепестка: а. - схема, высокоточного раскрытия. Этапы раскрытия: I - транспортное положение лепестка, II - этап пизкоточиого раскрытия, III - IV - эта.пві высокоточной фиксации конечного состояния, 1 - ось вращения лепестка, па. этапе раскрытия, 2 - ось вращения лепестка, при фиксации конечного состояния, 3 - У-образпые элементы опирания, 4 - шаровые опоры; в - физическая модель кинематической связки системы раскрытия лепестка. 5 - шаровые опоры, 6 - У-образпые пазы, 7 - имитатор лепестка, 8 - ось вращения имитатора, лепестка.

Рис. 10. Физическое моделирование системы раскрытия лепестка: а. - имитатор лепестка, в процессе раскрытия, в - имитатор лепестка, в раскрытом состоянии

• 5.    Заключение

Классические кинематические связки и их модификации открывают новые интересные возможности при разработке самоустанавливающихся замков для решения задач сборки и раскрытия составных твердотельных зеркал. В работе предложены новые конструкции самоустанавливающихся замков статически определимого типа для условий невесомости и представлены результаты их физического моделирования.