Математическое моделирование автономного мобильного робота с тремя всенаправленными колесами

Мобильные роботы обладают гораздо большей гибкостью и подвижностью, чем манипуляторы, что приводит к необходимости более сложных моделей. С точки зрения кинематики, основное различие между манипулятором и мобильным роботом заключается в характере и расположении его суставов [1]. Робот-манипулятор обычно моделируется как открытая кинематическая цепь, состоящая из чередования твердых тел с соединительными элементами одной степени свободы. В то время как кинематическая структура мобильного робота может рассматриваться как набор замкнутых кинематических цепей, таких как колесо, контактирующих с землей. Кроме того, взаимодействие колеса с землей определяется с кинематической точки зрения как плоское соединение с тремя степенями свободы, где одна из них, обычно неконтролируемая, представляет собой поперечное проскальзывание [2]. Эти два факта затрудняют построение модели.

Робот имеет несколько колёс с тремя степенями свободы (DoF) на каждом, что дает ему возможность маневрировать. В частности, у этого робота три колеса, каждое из которых имеет три степени резкости, и все они двунаправленные. На рисунке 1 отображена схема трехколесного робота.

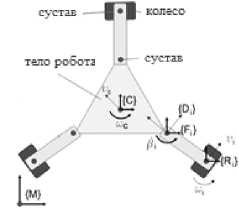
Рисунок 1 – Схема трехколесного робота

Система координат пола {M} фиксирована относительно поверхности и представляет собой систему координат для движения робота. Соответствующее глобальное положение робота представлено символом {C}, которое связано с телом робота; {Fi} – это i-й сустав ноги, прикрепленный к корпусу робота. λi описывает вектор положения робота. {Di} относится к компоненту направленности i-го колеса. Направленный угол обозначен βi. {Ri} представляет системы, расположенные в точке контакта с полом i-го колеса.

На основании уравнений линейной и угловой скоростей робота [1] и параметров всенаправленных колес [3], матрица Якоби будет выглядеть так:

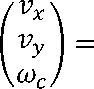
2R

—

\ 3L

R

V3

—R

—R

3L

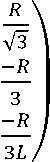
( ^ 1%\

• (^ 2% )

\ ^3%/

Якобиан обратного отображения (1) робота можно выразить следующим

образом:

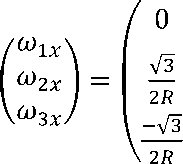
R

— 1

2R

— 1

2R

—L

R

—L

R

—L

R

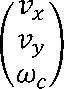
В качестве среды моделирования выбрана CoppeliaSim, в которую была перенесена Simulink-модель и 3D-модель робота и окружения, созданная в Blender. Исследуемая модель представляет собой голономную систему, допускающую всенаправленное движение и, следовательно, любую комбинацию угловой и линейной скоростей. Это позволяет роботу совершать любые движения по плоской поверхности.

На рисунках 2 и 3 представлены результаты, полученные при попытке осуществить моделью линейное и вращательное движения. Линейный тип

движения определяется линейной скоростью, описываемой компонентами v cx и

vcy. Эти компоненты должны быть постоянными, чтобы робот двигался

линейно, а угловая скорость θ c была равна нулю.

Рисунок 2 – Линейное движение робота

В случае вращательного движения робот вращается вокруг своей оси.

Компоненты v cx и v cy равны нулю, в то время как θ c остается постоянным.

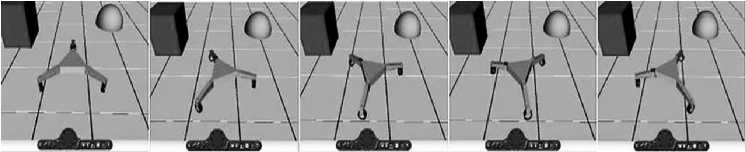
Рисунок 3 – Вращательное движение робота

Как видно на рисунках выше, робот может двигаться по любому пути в зависимости от скорости, изменяя которую, направление робота может меняться, заставляя двигаться к любой точке на плоскости.

На рисунке 4 представлен график, на котором отмечено желаемое движение робота (кривая) и фактическое движение робота (траектория движения робота).

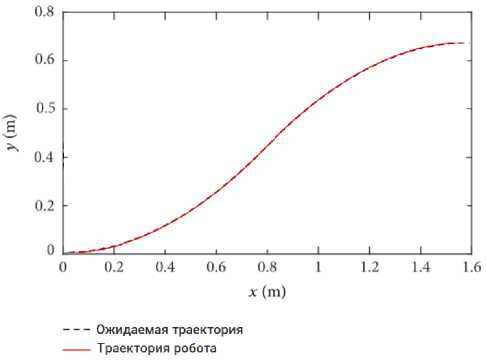
Рисунок 4 – Траектория движения робота по простой кривой

Как можно заметить из рисунка 4, траектория движения по простой кривой полностью совпадает с ожидаемой траекторией движения.

В данной статье был представлен расчет кинематическая модель трёхколёсного мобильного робота, оснащённого всенаправленными колёсами. Показаны прямая и обратная модели, необходимые для вычисления положения на основе скорости колес и скоростей, необходимых для достижения определенного положения соответственно. Была собрана модель, чтобы продемонстрировать

полную    функциональность

кинематического

моделирования для робота, в которой представленные результаты очень удовлетворительны. Были выполнены два основных движения (линейное и вращательное), а также реализовано криволинейное движение.