Математическое моделирование биомеханики бедренных компонентов проксимальной фиксации

Одним из важнейших этапов разработки и проектирования силовых имплантируемых конструкций является биомеханическое обоснование их работоспособности и надежности, т.е. способности материалов имплантата сопротивляться разрушению или необратимой деформации под действием функциональных нагрузок различного характера и величины [2, 11]. В настоящее время наиболее распространенным методом решения этой задачи является математическое (компьютерное) моделирование механического поведения системы «имплантат – структуры организма» в процессе или в результате нагружения. Широкие возможности современной компьютерной техники и программного обеспечения, мощный универсальный математический аппарат обеспечивают достаточную достоверность, оперативность и гибкость прогнозирования поведения таких систем с учетом влияния многих внутренних (структура системы, свойства материалов, условия взаимодействия компонентов системы на границах раздела и т.д.) и внешних (тип, величина, точки приложения нагрузок, ограничения перемещений точек и объемов системы и др.) факторов [6, 7, 14].

Математическое моделирование дает необходимую информацию для решения и другой, не менее важной проблемы – обеспечения механической совместимости имплантата, которая опреде- ляет возможность, продолжительность и результат адаптации структур организма к функционированию в новой биотехнической системе. Изменение биомеханики системы в результате имплантации конструкций для остеосинтеза, укрепления или замещения связочно-хрящевых структур, эндопротезов суставов и костей и т.д. может приводить и к изменению состава, структуры, объема, свойств костных и других тканей [12, 13]. Например, при исключении каких-либо объемов костных структур из процесса передачи силовых потоков (нагрузок) должен происходить их лизис, и, напротив, в случае чрезмерной концентрации механических напряжений (т.н. стресс-шилдинг) можно прогнозировать увеличение плотности и объема костной ткани в месте значительного превышения нормального уровня нагрузок [8, 9, 15]. В случае же, если механические напряжения превышают предел прочности костной ткани при данной схеме нагружения как для существенно анизотропных кортикальных костей, так и для квазиизотропных спонгиозных, следует ожидать разрушения кости, и в этом случае конструкция имплантата и/или выбор материала для нее являются неудачными.

В общем случае механическая совместимость имплантата может быть оценена по степени подобия напряженно-деформированного состояния и механического поведения биологических компонентов биотехнической системы (например, сохраненных при эндопротезировании сустава костных структур) состоянию и поведению соответствующей биологической системы в здоровом неповрежденном статусе при одинаковых функциональных нагрузках.

Математическое моделирование может также дать полезную информацию о поведении имплантата и взаимодействующих с ним структур организма в «нештатных» ситуациях, обусловленных, например, неточностями в планировании и технике проведения самой хирургической операции. Эта информация позволяет сформулировать дополнительное (к медицинским) «техническое» обоснование правильного выбора и точной установки имплантата [1, 3, 4, 6].

Очевидно, что «встраивание» математического моделирования в схему проектирования имплантата не только дает важнейшую информацию о функционировании системы «имплантат – структуры организма», но и позволяет создать эффективную обратную связь в самом процессе проектирования, обеспечивающую оперативную оптимизацию геометрических и/или физико-механических параметров имплантата. Причем «сигналом» к корректировке конструкции и выбору материала имплантата (или его структурного состояния, определяющего свойства), по нашему мнению, является даже не превышение механическими параметрами состояния компонентов биотехнической системы определенных критических значений, например, напряжений разрушения – в этом случае необходимость корректировки очевидна. Как показал наш опыт проектирования имплантатов с использованием компьютерного моделирования, а также опыт проведения технических и клинических испытаний, внесение изменений в конструкцию имплантата или его свойства целесообразно уже при уровне расчетных механических параметров в 70-80 % от

МАТЕРИАЛ

В настоящей работе методом конечных элементов с использованием программы ANSYS проведен анализ напряженно-деформированного состояния, возникающего при воздействии наиболее критичных функциональных нагрузок в системе «бедренный компонент эндопротеза тазобедренного сустава – костные структуры».

На первом этапе моделирования был разработан типоразмерный ряд анатомически подобных объемных моделей естественной и эндопротезированной ножкам "CORAIL" и "TAPERLOCK" (соответствующих типоразмеров) бедренной кости. Нагрузка прикладывалась к центру ротации суставной головки. Величина и направление действия нагрузки принимались соответствующими стандарту ISO 7206-4.3 на технические испытания ножек эндопротезов: R = 3300 H, угол с осью бедренной кости во фронтальной плоскости – 10°, в сагиттальной – 9° (рис. 1).

Типоразмер ножки при протезировании определяется (в числе других показаний для конкретного клинического случая) размерами бедренной кости, критических. Это обусловлено многими причинами и их возможным неблагоприятным сочетанием. Во-первых, ограничена точность результатов расчетов как возможностями самого применяемого математического метода, так и техники моделирования. По нашим оценкам, при приемлемом времени расчета варианта, определяемом сложностью созданной модели, абсолютная ошибка результата может составить 5-10 %. Кроме того, необходимо учитывать возможность превышения реальных нагрузок на имплантат по сравнению с расчетными, несовпадение реального положения имплантата с его «идеальной» установкой в модели, отличия в анатомии и свойствах структур организма от заданных в модели среднестатистических значений и многие другие факторы. Совокупное влияние этих факторов должно «компенсироваться» коэффициентом запаса надежности, который равен отношению «критического» параметра механического поведения данного компонента системы (напряжения или деформации разрушения, максимально допустимые смещения и т.д.) к соответствующему расчетному значению. По нашему мнению, этот коэффициент должен составлять не менее 1,3-1,5.

В настоящее время наиболее распространенным и эффективным численным методом анализа напряженно-деформированного состояния и механического поведения сложных многокомпонентных систем гетерогенного строения является метод конечных элементов (МКЭ). Для реализации этого метода объемная геометрическая модель системы разбивается на отдельные конечные элементы простой формы, формируя непрерывную конечно-элементную сетку. Не вдаваясь в подробности метода, исчерпывающе описанного в литературе [10], отметим лишь, что МКЭ является итерационным, т.к. решения (поэлементные напряжения, деформации, скорости деформации), полученные на каждом временном шаге, являются начальными условиями для очередного расчета.

И МЕТОДЫ в частности, геометрией костномозгового канала, определяемой по рентгеновским снимкам. Эти размеры связаны с другими антропометрическими данными, в том числе и весом человека. Путем статической обработки серии рентгеновских снимков были определены «средние» параметры бедренной кости, которые соответствуют и среднему весу человека 7580 кг. Длина такой среднестатистической бедренной кости составила 400-420 мм, офсет – расстояние от продольной оси бедра до центра бедренной кости (или центра ротации сустава) – 40-43 мм, диаметр костномозгового канала в истмусе – 12-13 мм.

Для полученной таким образом геометрии костномозгового канала наиболее вероятным является использование ножки "CORAIL" 10-го типоразмера или ножки "TAPERLOCK" 10-го типоразмера (рис. 2). Таким образом, был получен набор геометрических и конечно-элементных моделей систем «ножка эндопротеза – бедренная кость», а также соответствующий набор бедренной кости с естественным тазобедренным суставом. Мы модели- ровали несколько вариантов установки бедренных компонентов в костномозговой канал бедренной кости, рассчитали возможность установки бедренных компонентов проксимальной фиксации "CORAIL" и "TAPERLOCK" плотно на кортикальную кость, а также возможность фиксации данных компонентов в губчатой кости без контакта с кортикальной костью во фронтальной и сагиттальной плоскостях. Также мы провели анализ напряженно-деформированного состояния биомеханической системы «бедренная кость – ножка эндопротеза проксимальной фиксации "CORAIL" и "TAPERLOCK"» в условиях состоявшейся плотной остеоинтеграции данных бедренных компонентов в проксимальном отделе бедренной кости и в условиях, где остеоинтеграция отсутствует (в раннем послеоперационном периоде).

На рисунке 3 показаны конечно-элементные модели бедренной кости без эндопротеза в исход- ном ненагруженном состоянии и под действием результирующей нагрузки R = 3300 Н, приложенной в центре бедренной головки. Напряженно-деформированное состояние бедренной кости определяется сочетанием осевого сжатия и изгиба в направлении, близком к латерально-медиальному. Величина максимального прогиба кости и смещение головки бедренного компонента системы определяют жесткость естественной кости и системы с эндопротезом. Смещение центра ротации кости под воздействием нагрузки составляет 0,803 мм. Растягивающие напряжения в кортикальных структурах имеют максимальные значения в верхней трети бедренной кости с латеральной стороны и достигают для здоровой кости, соответствующей ножке 12-го типоразмера, 37 МПа, сжимающие силы распределены по дуге Адамса и достигают максимума (около 60 МПа) вблизи шейки бедра.

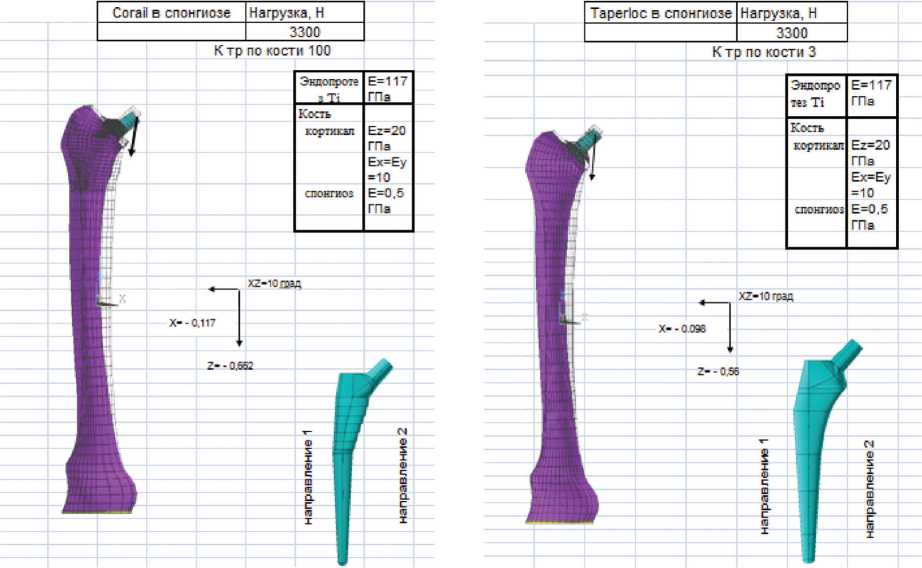
Деформация к.-э. модели ножки CORAIL (10:1)                        Деформация к.-э. модели ножки TAPERLOC (10:1)

и смещение центра ротации под действием расчетных нагрузок   а и смещение центра ротации под действием расчетных нагрузок О

Рис. 1. Математическое моделирование напряженно-деформированного состояния биомеханической системы «бедренная кость – ножка эндопротеза проксимальной фиксации "CORAIL" (а) и "TAPERLOCK" (б)»

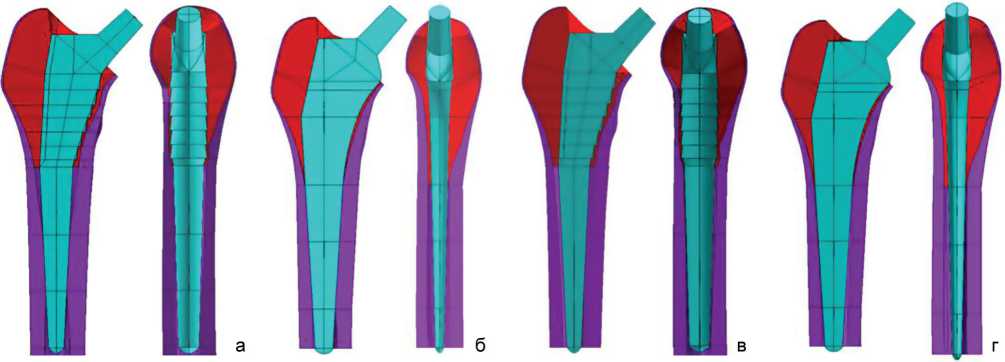
Рис. 2. Компьютерные модели бедренных компонентов (фронтальный и сагиттальный вид) "CORAIL" (а – в кортикале; б – в спонги-озе) и "TAPERLOCK" (в – в кортикале, г – в спонгиозе)

На рисунке 3 показаны конечно-элементные модели бедренной кости без эндопротеза в исходном ненагруженном состоянии и под действием результирующей нагрузки R = 3300 Н, приложенной в центре бедренной головки. Напряженно-деформированное состояние бедренной кости определяется сочетанием осевого сжатия и изгиба в направлении, близком к латерально-медиальному. Величина максимального прогиба кости и смещение головки бедренного компонента системы определяют жесткость естественной кости и системы с эндопротезом. Смещение центра ротации кости под воздействием нагрузки составляет 0,803 мм. Растягивающие напряжения в кортикальных структурах имеют максимальные значения в верхней трети бедренной кости с латеральной стороны и достигают для здоровой кости, соответствующей ножке 12-го типоразмера, 37 МПа, сжимающие силы распределены по дуге Адамса и достигают максимума (около 60 МПа) вблизи шейки бедра.

Таким образом, приведенная методика обследования пациентов позволила нам произвести анализ закономерностей как в клиническом и функциональном результате, так и в рентгенологических изменениях при эндопротезировании тазобедренного сустава с использованием бедренных компонентов проксимальной фиксации. Произведенные наблюдения позволили сделать выводы относительно особенностей применения бедренных компонентов данного типа.

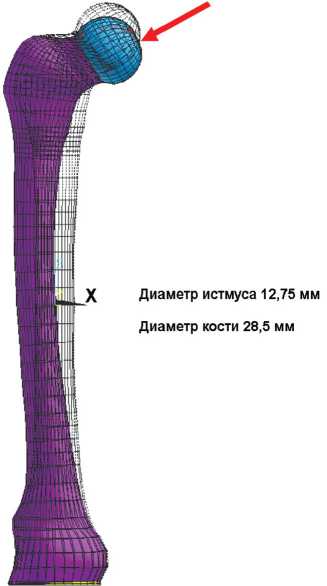
Рис. 3. Деформация конечно-элементной модели бедренной кости без эндопротеза и смещение центра ротации под воздействием нагрузки (R). Деформация (10:1) конечно-элементной модели бедренной кости при осевой нагрузке 3300 Н

РЕЗУЛЬТАТЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ

Нами оценивалось смещение центра ротации моделируемой системы под действием расчетной нагрузки Н=3300, прилагаемой под углом 10˚ (стоя на одной ноге). При этом мы оценивали смещение при вариантах проксимальной и промежуточной фиксации бедренных компонентов "CORAIL" и "TAPERLOCK". Каждый вариант рассматривался при различных коэффициентах трения по кости. Были просчитаны варианты плотной остеоинтеграции для каждого бедренного компонента. Также были просчитаны модели, имитирующие состояние сразу после имплантации бедренных компонентов, где остеоинтеграция отсутствует (табл. 1).

Анализ показателей выявил, что смещения при коэффициенте трения 100 значительно не отличается от аналогичных данных для естественной кости и подтверждает механическую совместимость бедренных компонентов "CORAIL" и "TAPERLOCK". В раннем послеоперационном периоде под нагрузкой 3300 Н возникают чрезмерные смещения, которые могут быть причиной развития асептического расшатывания – нестабильности бедренного компонента, независимо от поверхностной обработки имплантата (гидроксиапатит или пескоструйное напыление).

Результаты анализа напряженно-деформированного состояния: осевого напряжения в бедренном компоненте, в спонгиозе и в кортикале при различных коэффициентах трения приведены на рисунке 4.

Проведенные расчеты показали, что наибольшую величину, как и в случае здоровой бедренной кости, имеют осевые растягивающие и сжимающие напряжения. Они распределены соответственно с латеральной и медиальной сторон в верхней трети кости достаточно равномерно и подобно распределению напряжений без эндопротеза (исключая участок шейки бедра, который при эндопротезировании резецируется). При этом уровни напряжений в эндопротезированной и здоровой кости весьма близки при условии состоявшейся остеоинтеграции (Ктрения=100) (рис. 4). В данном случае, учитывая близость и других параметров механического поведения бедренной кости под нагрузкой, в частности, смещений центра ротации естественного и искусственного суставов, можно сделать вывод об адекватности механического поведения естественной и эндопротезированной бедренной кости. Однако этот вывод справедлив лишь при правильном выборе типоразмера бедренного компонента и точной его установке.

Таблица 1

Смещение моделей бедренных компонентов "CORAIL" и "TAPERLOCK" под нагрузкой 3300 Н, приложенной под углом 10˚ по осям Х и Z при различных коэффициентах трения по кости

	"CORAIL"				"TAPERLOCK"
	в спонгиозе		в кортикале		в спонгиозе		в кортикале
Нагрузка	3300Н
К трения по кости	100	1	100	1	100	3	100	3
Х	-0,117	-0,121	-0,1	-0,1	-0,089	-0,098	-0,086	-0,086
Z	-0,062	-0,676	-0,6	-0,537	-0,51	-0,56	-0,49	-0,49

«CORAIL» в спонгиозе (Ктр=100)

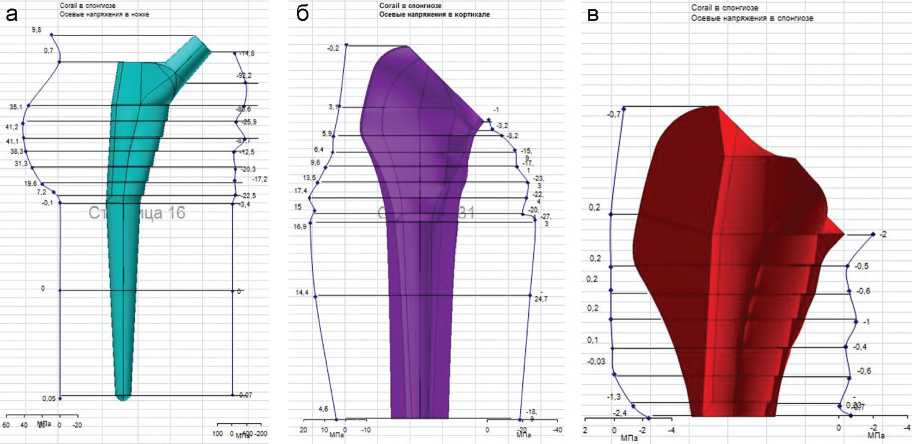
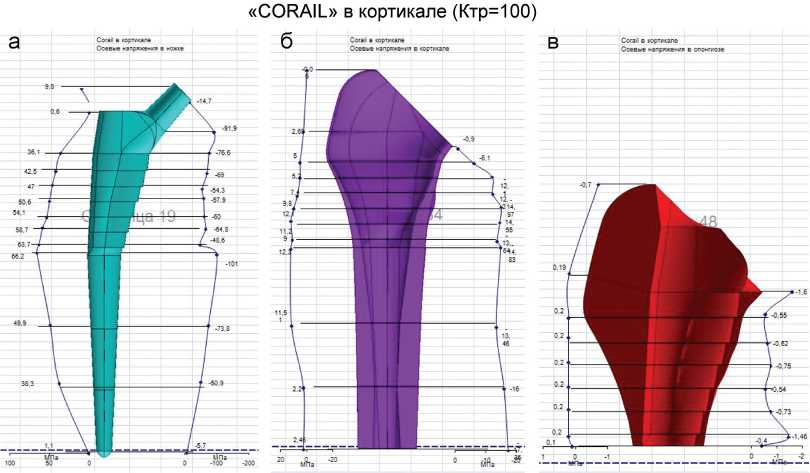
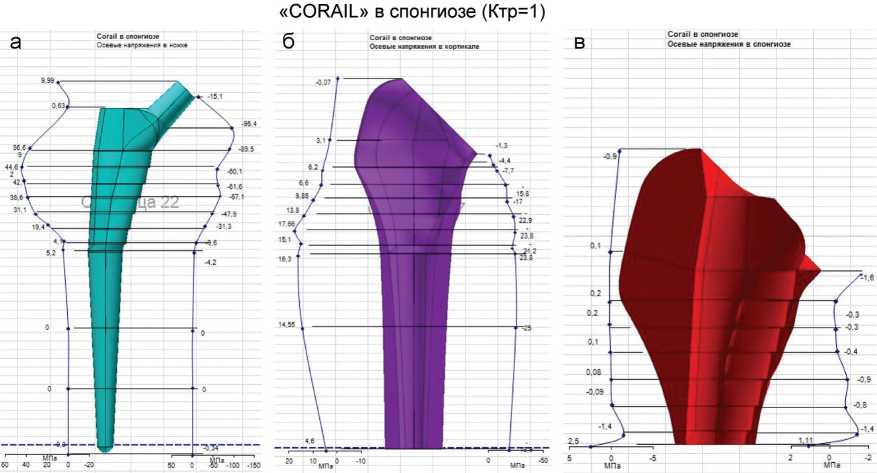
Рис. 4. Характер распределения напряжений в системе «имплант-кость (в кортикале и в спонгиозе)» при различных вариантах имплантации бедренных компонентов, на примере "CORAIL" и "TAPERLOCK" и при различных коэффициентах трения: а – осевые напряжения в ножке; б – осевые напряжения в кортикале; в – осевые напряжения в спонгиозе

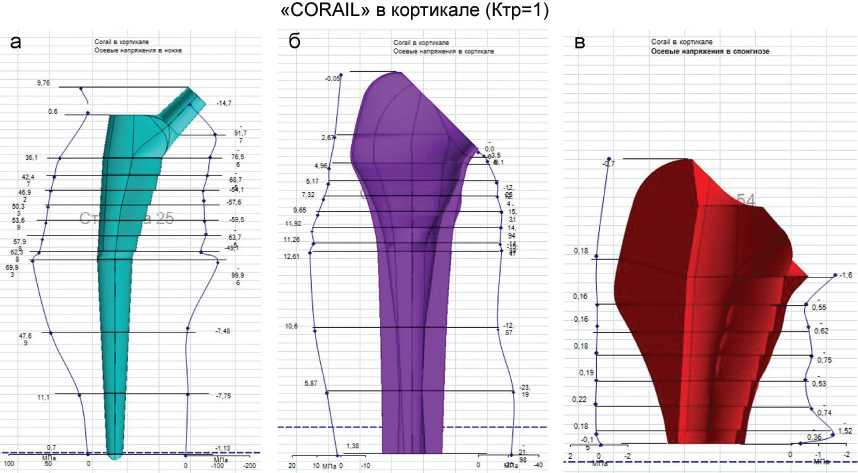
«TAPERLOCK» в спонгиозе (Ктр=100)

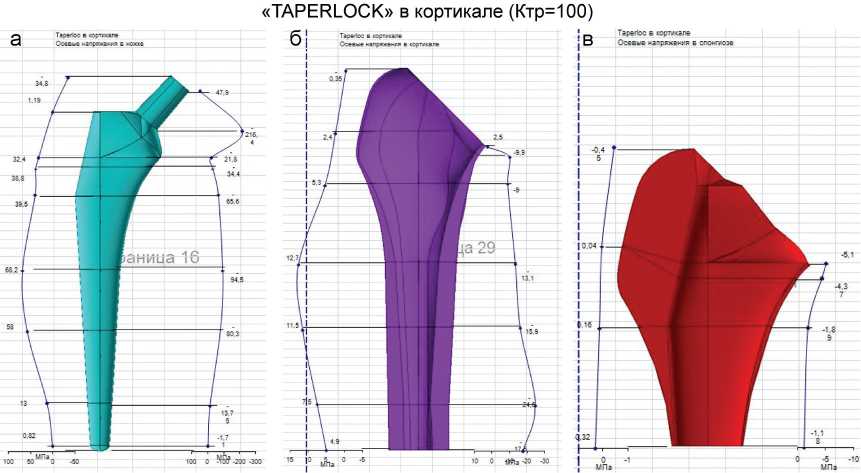
Продолжение рис. 4. Характер распределения напряжений в системе «имплант-кость (в кортикале и в спонгиозе)» при различных вариантах имплантации бедренных компонентов, на примере "CORAIL" и "TAPERLOCK" и при различных коэффициентах трения: а – осевые напряжения в ножке; б – осевые напряжения в кортикале; в – осевые напряжения в спонгиозе

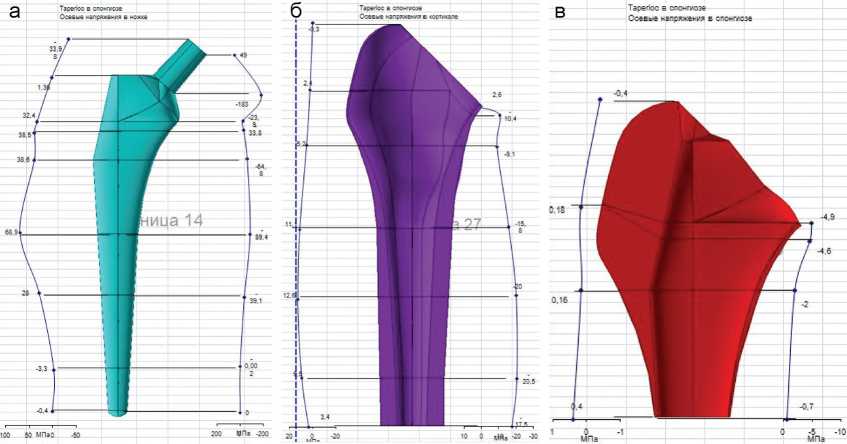
«TAPERLOCK» в спонгиозе (Ктр=3)

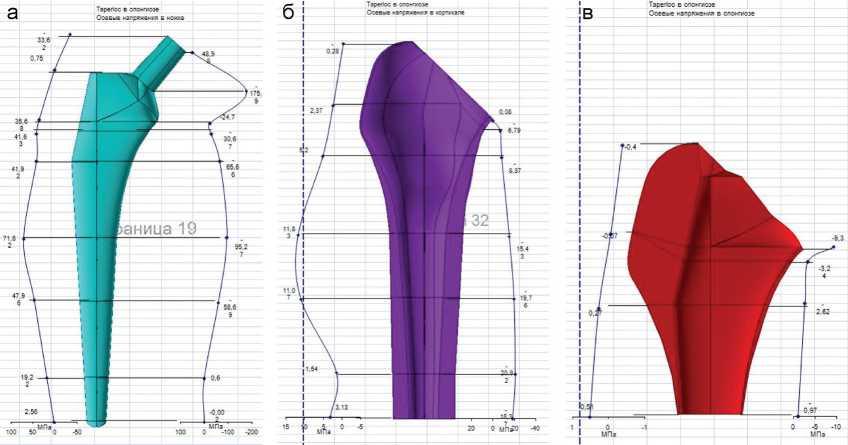
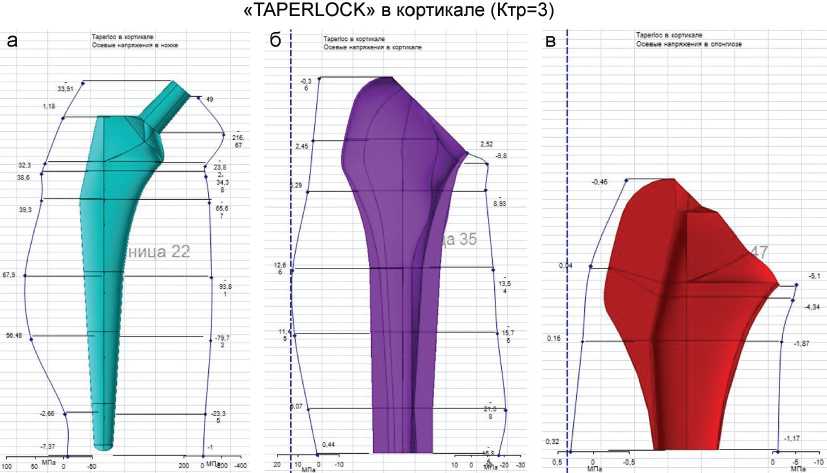
Продолжение рис. 4. Характер распределения напряжений в системе «имплант-кость (в кортикале и в спонгиозе)» при различных вариантах имплантации бедренных компонентов, на примере "CORAIL" и "TAPERLOCK" и при различных коэффициентах трения: а – осевые напряжения в ножке; б – осевые напряжения в кортикале; в – осевые напряжения в спонгиозе

Анализ напряжений и деформаций в ножках эндопротезов под действием расчетной результирующей нагрузки дал следующие результаты:

– максимальные растягивающие напряжения достигаются на латеральной поверхности шейки и в зоне перехода клинообразной дистальной части ножки в проксимальную (переход «клин – дуга Адамса»);

– максимальные сжимающие напряжения создаются на медиальной поверхности шейки и ножки.

При нагрузке 3300 Н неизбежно смещение бедренного компонента относительно костных структур в цикле «нагрузка – разгрузка – нагрузка». Микроподвижность ножки должна компенсироваться упругой деформацией кости, прилегающей к поверхности ножки. Это может быть достигнуто в том случае, если параметр шероховатости поверхности ножки значительно превышает расчетную амплитуду осевого смещения. Поэтому при анализе работы системы рассчитывались относительные смещения ножки в цикле «нагрузка – разгрузка – повторное нагружение» и неизбежно возникающие радиальные напряжения на границе «ножка эндопротеза – кость». Относительное смещение ножки по длине при ее первичном нагружении составляет 0, 358 мм и 0,347 мм в 3 и 5 зонах по Gruen соответственно. При снятии внешней нагрузки (цикл разгрузки) под действием упругих радиальных сил ножка «стремится» занять исходное положение, чему препятствуют силы трения на контактных поверхностях. Максимальная амплитуда возвратных смещений в зоне контакта ножки с кортикальной костью для всех типоразмеров составляет 5-7 мкм с медиальной стороны и 2-10 мкм – с латеральной. При повторном нагружении системы амплитуда циклических смещений в зоне первичной фиксации составляла: для медиальной стороны 4 мкм, а для латеральной – 7 мкм. Наименьшая амплитуда циклических смещений отмечена в 3 и 5 зонах по Gruen.

ЗАКЛЮЧЕНИЕ

Полученные результаты математического моделирования биомеханики бедренных компонентов, на примере "CORAIL" и "TAPERLOCK", позволили сделать следующие заключения:

– увеличение шероховатости поверхности (Rz = 30-60 мкм), а, соответственно, и коэффициента трения контактных поверхностей ножки должно приводить к снижению как осевого смещения ножки относительно костных структур, так и общего уровня радиальных напряжений, частично определяемых этим смещением;

– осевые напряжения, концентрирующиеся в бедренной кости с имплантированным бедренным компонентом проксимальной фиксации, и смещение центра ротации при нагрузке 3300 Н близки к таковым здоровой кости при условии состоявшейся остеоинтеграции (отсутствует плотный контакт имплантата с кортикальной костью);

– осевые напряжения, концентрирующиеся в бедренной кости с имплантированным бедренным компонентом проксимальной фиксации, и смещение центра ротации при нагрузке 3300 Н намного больше в раннем послеоперационном периоде (отсут- ствует плотный контакт имплантата с кортикальной костью), что может быть причиной асептического расшатывания имплантата;

– наибольшие тангенциальные и радиальные напряжения возникают в 3 и 5 зонах бедренной кости, что соответствует уровню первичной фиксации эндопротеза (плотный контакт имплантата с кортикальной костью). При этом не отмечается полной «разгрузки» 1, 2, 6, 7 зон по Gruen, что способствует нагружению проксимального отдела бедренной кости и снижению проявлений stress shielding.

Таким образом, полученные данные позволяют прогнозировать стабильную первичную фиксацию эндопротеза на начальном этапе его функционирования в организме человека при плотной посадке на кортикальную кость, но менее физиологичной в отношении распределения нагрузки. При неплотной посадке бедренных компонентов на кортикальную кость страдает инициальная стабильность, но в условиях состоявшейся остеоинтеграции распределение нагрузок происходит более физиологично, что прогнозирует долгосрочную выживаемость имплантата.