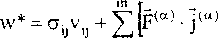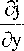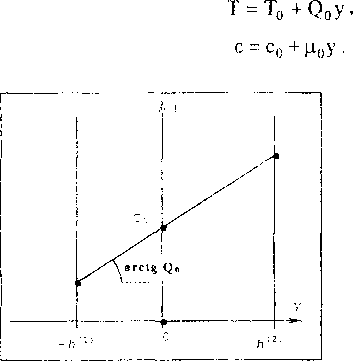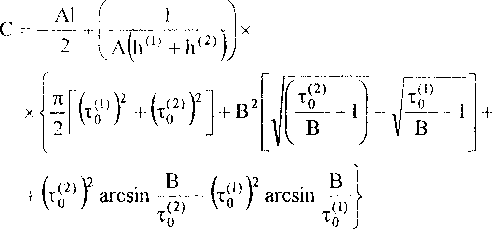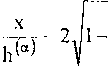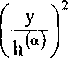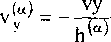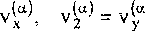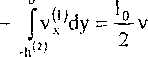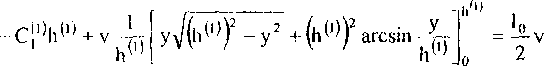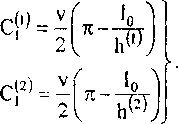Тогда уравнение притока тепла (1.4) примет вид рТ— -pq-div q-^p(a)j(a) нстуу|Гг у А UL V Ct=l ) a=l
Из (1.3) и (1.4) получим dt dt u lJ J
Учитывая выражение функции рассеивания (9), находим из (12)
РУ = РТ^ -1 ^^^"^ ^^'gr3d^“^ R или,сравнивая с (1 9)
(Ю)
(Н)
de ds A (a) dc( ’ dt dt ~( dt
то есть получаем формулу Гиббса [5], которую можно записать в виде
de-Tds-^ydc^. °5)
Для описания процессов термодиффузии кроме уравнений притока тепла (11) и диффузии (1.5) необходимо использовать определяющие соотношения, связывающие тепловые и диффузионные потоки, с одной стороны, и градиенты температуры и химических потенциалов — с другой.
Принимая эти соотношения линейными и удовлетворяющими условиям Онзагера [4], их можно записать в виде
— _ д Т ^^
a=l
p=i
Если коэффициенты связанности A-“’ отсутствуют, то соотношения (16) совпадают с законом теплопроводности Фурье, а соотношения (17) - с обобщённым законом Фика
Поэтому тензор Л . можно назвать тензором теплопроводности, а тензоры в(“№) -тензорами коэффициентов диффузии. Для изотропной среды эти тензоры являются шаровыми [3]:
Лу = Лбу, D^ = О(аХР,бу .
В силу соотношений (8) число независимых парциальных коэффициентов диффузии
D(aXP) с nF может быть сокращено до (/и -1)2
Если попытаться приспособить создаваемую модель для описания обработки материалов, то к описанной системе уравнений следует добавить уравнения движения сплошной среды (1.2) Считая процессы квазистатическими, можно рассмотреть уравнения равновесия
Т.|Ч>1;; О(19)
Механические свойства среды должны быть заданы дополнительно, хотя из предыдущего можно понять, что речь пойдёт о несжимаемой вязкой жидкости. Действительно, только для модели вязкой жидкости диссипация имеет вид [2]
w - GyV,(20)
причём под ст понимаются "вязкие" напряжения, т.е. рассматривается случай несжимаемой жидкости, для которой уравнение неразрывности (1.1) имеет вид divv = 0.(21)
Заметим, что при отсутствии диффузионных эффектов функция рассеивания (9) совпадает с (20). Если не рассматриваются процессы разгрузки, то законы пластического течения, используемые в технологических задачах обработки материалов, совпадают с законами вязкой жидкости, вообще говоря, нелинейной.
Будем считать, что рассматриваются квазилинейные, т.е. тензорно линейные определяющие соотношения [3]. Тогда для замыкания системы уравнений, т.е. для полного описания модели среды введём, например, следующие определяющие соотношения:
aij ~ Cyki(")vki ’(22)
№
5 = al а=1
111(24)
Р=1
Здесь a, ba, dНетрудно видеть, что определяющие соотношения (23) не противоречат формуле Гиббса (15).
Если теперь подставим определяющие соотношения (22) в уравнения равновесия (19), то получим три уравнения равновесия относительно трёх компонент вектора скорости v. Подставляя определяющие соотношения (24) в соотношения(16), (17), а результат и (23) в уравнения диффузии (1.5) и уравнение притока тепла (11), будем иметь систему (ш-1)+1 = ш уравнений для определения (^-1) независимых концентраций с<а) и температуры Т . В случае несжимаемой среды нужно ещё найти давление для чего необходимо воспользоваться уравнением неразрывности (21). Таким образом, мы получили замкнутую систему уравнений.
Сюда требуется добавить начальные данные:
t=:O:T = T0, с(а)=с<,а)
и граничные условия, например где Тс - температура окружающей среды; ц^ - химический потенциал р -го компонента окружающей среды, Р - коэффициент теплообмена, а уар - коэффициенты массообмена.
§3 . Осаживание композиционной полосы
Рассмотрим простейший пример. Пусть длинная полоса шириной 1, состоящая из двух слоёв разного материала, осаживается двумя жёсткими плитами с силой 91 (рис. 1).
Рис. 1. Схема к постановке задачи
Будем считать, что длина полосы L (перпендикулярно плоскости чертежа) много больше её ширины 1, которая в свою очередь много больше высоты
h - 1г') +h^’.
Ширина и высока полосы изменяется в плоскости х, у. Все величины, относящиеся к первому материалу (выше оси х), будем снабжать верхним индексом (1), а относящиеся ко второму материалу (ниже оси х) -индексом (2).
В силу условий (1) задачу для термодиффузионного процесса можно считать одномерной. Тогда из (2.16), (2.17) имеем
. 6Т си q = -Л--------А — , Эу бу i = -A— ду- бу
а из (2.23) и (2.24)
s = а Г + Ьс ц = ЬТ + de.
Уравнение диффузии (1.5) можно записать в виде
de dj р——T + R dt бу
а уравнение притока тепла (2.11) в виде
„ d s dq д / Л . дц „ рТ—= pq0 - —+ —(m)+cv-j — -R .
dt оу бу dy
Рассмотрим самый простейший случай. Для этого предположим: а) химические реакции отсутствуют: R, = О, R = 0;
б) используется линеаризованное уравнение (7), для чего все нелинейные слагаемые отброшены;
в) массовый источник тепла отсутствует: q0 = 0;
г) нет зависимости от времени, поэтому рассматриваем стационарный (установившийся) процесс. Тогда уравнение диффузии (6) даёт
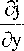
=> j = const,
а уравнение притока тепла (7) - ду
q = const.
Поэтому из (2)-(5) имеем (рис 2, 3)
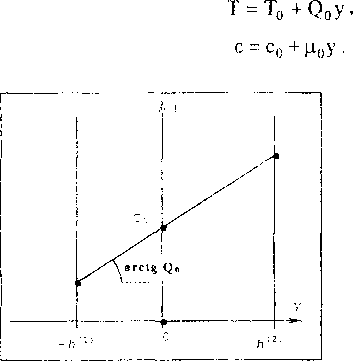
(Ю)
(И)
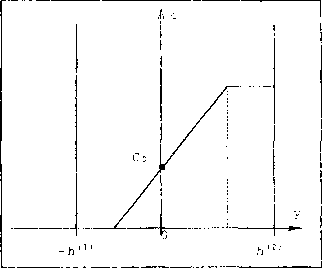
Рис 2. Распределение температуры Рис.З. Распределение концентрации
Рассмотрим теперь механическую задачу. Будем считать предел текучести каждого материала Тда)(а = 1, 2) известной функцией температуры Г и концентрации компонентов (с^с,, с3=1-с).
Тогда для каждого материала а = 1,2 имеем уравнения равновесия (2 19):
Эх Эу
Эо<а) Эола) ху+у _ Q
Эх Эу где для компонент тензора деформации используем обозначения [6]:
Оц=Ох, сг22-оу> а12=оху. (13)
Условия пластичности примем в виде [6]
^“)-ow)2+4(a<«))2(И)
а определяющие соотношения (2.22) - в виде qW^^w v(«)_v(«)(15)
у х у 2о(а) ~ v(«)■ v ху
Условия несжимаемости дают vСчитая жёсткие плиты шероховатыми, запишем при у ^(- ly^hi"); o^ = 41f^^(17)
Тогда принимая гипотезу Прандтля [7], что ст зависит только от у, получим из (12) и (14):
о^ лхСгг^^, ау = а6' = о<2) = -С - Ах ,
«ху "аху = 0^ = Ау + В, где постоянные А и В определяются из граничных условий (17):
А т^н-т^ е/^Ф^(19)
"hw+hw ~ h(i)+h(2>’ а постоянная С находится из интегрального условия
Оh<‘>
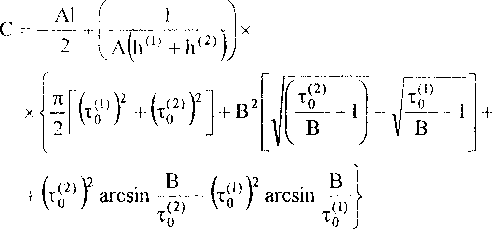
Силу, действующую на слой, можно найти по формуле
9? = 2f)cjdx = 21 С + А—
О •
Для построения кинематики (вектора скорости) воспользуемся соотношениями (15)
и (16). Нетрудно видеть, что они будут удовлетворены, если положить
у(«) = с(«) + v
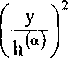
где
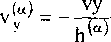
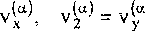
a v - заданная скорость сближения жёстких плит.
Постоянные С^ могут быть найдены из условия равенства потока материала, проходящего через сечение х = 0, количеству материала, выдавливаемого на длине 1 при сближении плит, т.е.
h", ' I
- fv^dy^v о 2
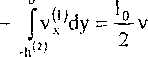
Подставляя (23) в (25), получим
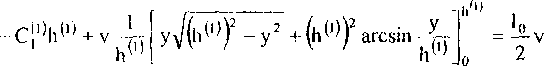
те.
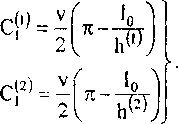
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (96-01-0084), а также Федеральной целевой программы "Интеграция" (проект №426).