Математическое моделирование динамического поведения дизельгенераторной установки с двухкаскадной системой амортизации

Работа дизельгенераторной установки (ДГУ) сопровождается широким спектром колебательных процессов, различных по амплитудным и частотным параметрам. Это предопределяет высокий уровень динамических напряжений, возникающих в элементах конструкции ДГУ, и влияет на их прочность, надежность и долговечность. Современные конструкции ДГУ имеют узлы (резинометаллические амортизаторы), обладающие конечными значениями жесткости и массы. В результате приложения внутренних нагрузок при эксплуатации ДГУ будут возникать конечные деформации упругих элементов, что при определенных условиях приведет к вибрациям с большими амплитудами или к потере устойчивости процессов динамического деформирования.

В процессе проектирования амортизирующего крепления большое значение имеет выбор параметров и оптимальной схемы расположения амортизаторов. При большом разнообразии схем размещения амортизаторов следует предпочесть такую, при которой центр тяжести амортизируемого агрегата совпадает с центром жесткости амортизирующего крепления [1]. Такая схема обеспечивает меньшую ширину спектра частот свободных колебаний и большая устойчивость амортизируемого агрегата. Однако из условий компоновки расположения опор

агрегата центр жесткости упругого основания не всегда совпадает с центром тяжести амортизируемого агрегата, но находится на одной вертикали с ним. И чем меньше будет расстояние между этими центрами, тем лучше. При таком положении центра жесткости и центра тяжести агрегата частоты поступательных и поворотных колебаний относительно горизонтальных осей будут попарно связаны, т.е. будут представлять собой двухсвязные колебания, а частоты вертикальных поступательных и поворотных относительно вертикальной оси колебаний будут независимыми. Сближение центров жесткости амортизирующего крепления с центром тяжести агрегата способствует увеличению устойчивости механизма и малому разбросу частот свободных колебаний.

По этой причине желательно возможно большее снижение частот свободных колебаний амортизированного механизма. Однако с уменьшением частоты свободных колебаний уменьшается жесткость амортизаторов, что приводит к снижению допускаемой статической нагрузки на амортизатор и увеличивает амплитуду колебаний амортизированного механизма. Поэтому в случае невозможности подбора необходимого количества и расположения амортизаторов для улучшения вибрационной защиты применяют двухкаскадные системы амортизации (Рис. 1).

При проектировании подвески ДГУ, т.е. при выборе жесткостных характеристик резинометаллических амортизаторов, а так же при расчете их количества и точек установки, наиболее важным является этап прогнозирования динамических перемещений, вибраций с большими амплитудами или к потере устойчивости процессов динамического деформирования. Особую важность принимают эти вопросы при решении задач структурной и параметрической оптими-

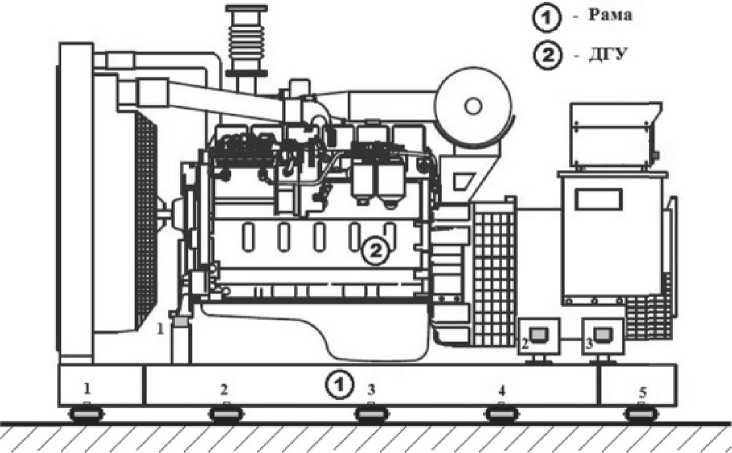
Рис. 1. Дизельгенераторная установка с двухкаскадной системой амортизации

зации конструкций амортизационного крепления ДГУ с целью снижения динамических перемещений, а также уровня излучаемого шума.

При исследовании колебательных процессов ДГУ как механической системы необходимым условием является понимание деталей ее динамического поведения при действии возбуждающих сил, приложенных в различных точках системы. Двухкаскадные системы в силу большего количества элементов, входящих в систему, представляют более сложный объект для исследования. Для решения этой задачи использовались различные подходы, включая прямое получение необходимой информации путем замеров, математическое моделирование и точное решение дифференциальных уравнений движения, дискретное моделирование с помощью конечных элементов и решение результирующей системы дифференциальных уравнений второго порядка.

В данной работе рассматриваются следующие задачи: моделирование и анализ динамического поведения ДГУ как пространственной двухмассовой системы; разработка алгоритма и программного комплекса на его основе, позволяющего производить расчет собственных частот колебания рамы и ДГУ и построение амплитудно-частотных характеристик перемещений рамы и ДГУ.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИЗЕЛЬГЕНЕРАТОРНОЙ УСТАНОВКИ

С ДВУХКАСКАДНОЙ СИСТЕМОЙ АМОРТИЗАЦИИ

Представим ДГУ с рамой как систему, состоящую из двух абсолютно жестких тел [2] (Рис. 2). Принимаем следующие допущения:

. резинометаллические амортизаторы ра- ботают в области малых упругих деформаций, жесткостная характеристика линейная;

. при внутреннем возбуждении ДГУ, определяемым неуравновешиванием двигателя демпфирование резинометаллическими амортизаторами незначительно;

. дизельный двигатель и генератор жестко связаны между собой и моделируются на эквивалентной расчетной схеме единой массой;

. каждая масса эквивалентной расчетной схемы имеет 6 степеней свободы;

. деформациями рамы, корпусных элементов дизеля и генератора пренебрегаем.

Введем неподвижную глобальную систему координат OXYZ. Кроме того введем локальные системы координат O 1 X 1 Y 1 Z 1 и O 2 X 2 Y 2 Z 2 для тел 1 и 2 соответственно. Точки O 1 и O 2 совпадают с центрами тяжести тел. Тело 1 (рама) установлено на упругих амортизаторах, имеющих

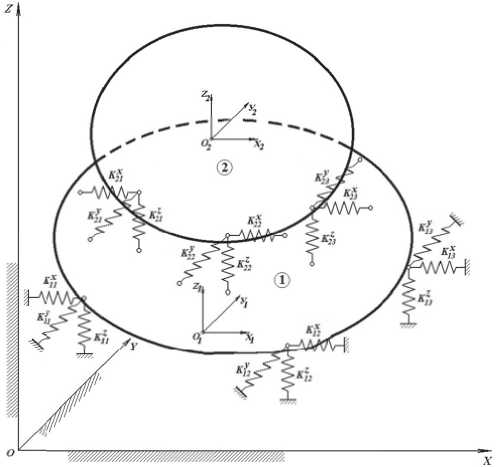
Рис. 2. Пространственная механическая система с упругими связями коэффициенты жесткости Kxi, Kyi и Kz1. Число амортизаторов первого ряда равно п1. Тело 2 (ДГУ) крепится к телу 1 на амортизаторах с коэффициентами жесткости Kx2, Ky2 и Kz2, число которых равно п2. Положение каждого i-го тела в глобальной системе координат определяется координатами центра масс (xi, yi и zi) и углами поворота локальной системы координат этого тела (фxi, фyi и фzi).

Математическая модель, описывающая динамическое поведение приведенной выше пространственной двухмассовой системы с упругими связями, представляет собой систему дифференциальных уравнений. Число уравнений равно 2*Ns, где Ns=6 - число степеней свободы для одного тела.

В матричном виде система дифференциальных уравнений имеет вид:

[ M ]{^}+[ K ]{q }={Q }, (1)

где [ M] - матрица масс,

[ K ] - матрица жесткости, { q } - вектор координат, { q } - вектор ускорений,

{ F } - вектор внешних сил.

Вектор координат формируется в виде:

^{ q ^} = [ ^Х 1 , y, z i , j xi , j yi , j zi , ^x 2 , У₂, z 2 , ф X2 , ф y2 , ф Z2 F- ⁽²⁾

Вектор { F } формируется за счет неуравновешенности вращающихся деталей силовой установки. Поэтому внешнее воздействие является функцией времени, и его частота совпадает с частотой вращения коленчатого вала двигателя.

Матрица масс:

^[ M = diag^[ m i , m i , m i , J xi , J y, , J i , m 2 , m 2 , m 2 , J x2 , J, J ^], (3) где m₁ и m₂ - массы рамы и силовой установки соответственно;

J xi , J yi J и J xi , J yi , J zi - моменты инерции рамы и силовой установки соответственно.

Матрица жесткости [ K ] является симметричной матрицей ( K_ij=K_ji ), ее формирование зависит от коэффициентов жесткости амортизаторов и их расположения в локальной системе координат:

n1n2

К1,1 = S k2 + S kXj i=1j n1n2

К ₆ = - У kxly - У МД, , К . = 1 , 6                 1i 1i             2j 2j       1 , 7

j = 1

i = 1

n2

К1,11 =- S k 2 j12 j ’ j = 1

n1           n2

’ ^K 1 , 5 = S ^kH^l Zi ⁺ S ^k2j l Zj ’

i = 1

j = 1

n2

- S kj j=1

n2

K1,12 = S k2 JXi ’ j = 1

К,2 = К,3 = К1,4 = К,8 = К1,9 = К1, 10 = 0 , n1           n2

- S k»1»" S ВДг i=1             j = 1

n1n2

к 2,2 = S ky + S к^’К 2,4 = i = 1j n1n2

К ₆=У k y l x + Tk y l

2 , 6               11 11               2 j *

j = 1

n2

- S k 2j ’ j = 1

x

2j ’ ^K 2 , 8

n2

^К 2 , 12 = S ^k2j^l2j ’ j = 1

К2,3 = К2,5 = К2,7 = К2,9 = К2,11 = 0 , n1        n2n1

n2

К 3 , 4 = S k 1i l 2i + S ky 2j ’

К ,=y k z + У k 3 , 3               11

i = 1          j = 1

n1

К

К

: 2) ’ n2

■35 =-У k^JXi -У kzl 3,5                 Z1 11              2 j

i = 1

n2 zy

3 , 10      S 2j 2j

j = 1

’ ^К 3 , 11

i=1j n2

'2j ’ К3,9 =- S k2j ’ j = 1

n2

j = 1

К = КК == К, ,= К _п

3,6       3,7        3,83,12

= S k lj l Xj ’ j = 1

= 0 ,

nl

n2

км = S kfi(l^i)2 + S k^Clip2 + i=l nln2

+ S kii(lfi)2 + S k^Cl^)2, i=l

К 4 , 5 =

К 4 , ₆ =

^^^^B

j=l n1 zxy

S ^k1i^l1i^l1i i = 1

n1 yxz

S ^k1i^l1i^l1i

^^^^B

i = 1

n2

К4,8 = S k22jl"Zj ’ К j=1

n2

n2

S k2jl2jl2j ’ j=1

n2

yxz

S k2jl2jl2j ’ К 4,7

j = 1

n2

zy

4,9     S 2j 2j ’ j=1

n2

К4,10 =- S k2j (l2j)2 - S k2j (l2j )2 ’ j=1j n2n2

к 4 И = У kZilXiVyi , K₄ = = У kyjixrzj , 4 , 11            2 2 j 2 j 4,12             2 j 2 j 2

j=1j nln2

k5,5=S kXi(l.i)2+S kx^l^)2 + i=ll nln2

+ S kn(ln)2 + S ki^lxp2, i=l

К, ^ 5 , 6

К 5 , 7 =

^^^^B

^^^^B

j=l n1n2

xyzx yz

S П,Н1,Н1,Н   S n'2jl2jl2j ’ i=1j n2

S k^zj ’K5,8 = 0 ’ j=1

n2

К5,9 = S k2zjl2j ’ j = 1

n2

n2

zxy

^К 5 , 10    S k 2 j l 2 j l 2 j ’

К

5 , 11 =    S ^k 2j ^ ^l^ Zj ⁾

j = 1

n2 xyz

К 5,12   S k2jl2jl2j ’ j=1

nl                n2

j = 1

n2

- S k z^ l ^l2j > ² , j = 1

К -Vky x 2+Vky x 2

^6,6 = S kli(lli) + S k2j(l2j) + i=l                     j=l nl                 n2

+ V k^x y ² + V k^x y ²

⁺ S ^kli^(lli^{) +} S ^k2j^(l2j⁾

i = l

j=l n2

К 7=y kXJXi, 6 97   ^^ 2j 2j j = 1

n2

К6,8 =-Sk2jl2j,K6,9 = 0’ j=1

n2

n2

yxz       xyz

К 6,10   S k2jl2jl2j ’К 6,11   S k2jl2jl2j ’ j=1

j = 1

n2               n2

К, 12 = -У k y ( l xi ) 2 - ТЛп ( l yi ) 2 ’ ⁶ , ¹²      ^^ 2.1^х 2j'     ^^  ²j^x 2j'

. j = 1                     j = 1

К , 7 =	— К1 , 7 ’	К 7 , 8 = К 7 , 9 = К 7 , 10 = 0
К7,11 =	- К1,11	К = -К ’ 7,12            1 ^ 12 ’
К8,8 =	- К2 , 8 '	К8 , 9 = К8 , 11 = 0 ,

8,10           2,10 ’    8,12           2,12 ’ л9,9      3х 3,9 ’ ^9,10      3v0,10 ’

К9,11 =   К3,11 ’ К9,12 = 0 ’ n2                n2

к 10,10 = Zkjlj2 + Zk2j(lj2 ’ j=1                    j=1

^К10,11 =

n2

-У k'lxvy.

2j 2j 2j j=1

К10,12

n2

- УкУУ'

2j 2j 2j j=1

n2n2

x z2z x2

K 11,11 = Z k2j (l2j ) + Z k2j (l2j ) ’ j = 1j

^K11,12 =

n2

- Z k2jlyyjl2ij j = 1

n2n2

к 12 = Vk y ( l xi ) ² + У k x ( l yi ) 2 ■ ⁶ , 12   ^^ ²I^х 2j'    ^^  ²I^х 2j'

. j=1j

В формулах (4) l^x₁ , l^y₁ , l^z₁ , и l^x₂ , l^y₂ , l^z₂ – координаты крепления амортизаторов рамы и ДГУ в их локальных системах координат.

РЕЗУЛЬТАТЫЧИСЛЕННОГО ЭКСПЕРИМЕНТА

Для решения системы дифференциальных уравнений (1) в настоящей работе применяется метод временных конечных элементов [3]. Проверка работоспособности метода проводилась на трехмассовой системе с упругими связями, для которой имеется точное аналитическое решение [4]. Кроме того, предлагаемая методика использовалась при моделировании динамического поведения элементов ходовых систем гусеничных машин [5, 6].

На основе изложенного алгоритма был разработан программный комплекс, который позволяет моделировать динамическое поведение ДГУ при любой частоте воздействия. Для известных параметров ДГУ и рамы, а также параметров амортизационного соединения вычисляются динамические перемещения центров масс элементов системы и углы поворота тел относительно осей глобальной системы координат. Задавая приращение частоты внешнего воздействия с определенным шагом, можно вычислить максимальные амплитуды динамических перемещений. Это позволяет строить амплитудно-частотные характеристики ДГУ и рамы. Кроме того, в

Таблица 1. Параметры дизельгенераторной установки

1 локальная подсистема: Рама
Масса m i , кг		Момент инерции J xi , кг*м2		Момент инерции J yi , кг*м2		Момент инерции J zi , кг*м2		Координаты центра масс
								x , м	У , м		z , м
290.000		24.212		102.239		117.825		-0.435	0.079		0.180
Параметры амортизационного крепления
№	Коэффициенты жесткости						Координаты крепления
	k xi , кН/м		k yi , кН/м		k zi , кН/м		l xi , м	l yi , м		l zi , м
1.	2646		1078		3871		-1.370	-0.380		0.000
2.	2646		1078		3871		-1.370	0.380		0.000
3.	2646		1078		3871		-0.532	-0.380		0.000
4.	2646		1078		3871		-0.532	0.380		0.000
5.	2646		1078		3871		0.148	-0.380		0.000
6.	2646		1078		3871		0.148	0.380		0.000
7.	2646		1078		3871		0.348	-0.380		0.000
8.	2646		1078		3871		0.348	0.380		0.000
9.	2646		1078		3871		0.548	-0.380		0.000
10.	2646		1078		3871		0.548	0.380		0.000
2 локальная подсистема: ДГУ
Масса m 2 , кг		Момент инерции J x2 , кг*м2		Момент инерции J y2 , кг*м2		Момент инерции J z2 , кг*м2		Координаты центра масс
								x , м	У , м		z , м
1683.000		177.114		723.428		673.264		-0.200	0.000		0.145
Параметры амортизационного крепления
№	Коэффициенты жесткости						Координаты крепления
	kx 2 , кН/м		ky 2 , кН/м		kz 2 , кН/м		1 x2 , м	l y2 , м		lz 2 , м
1.	3920		882		7056		-1.447	-0.387		-0.100
2.	3920		882		7056		-1.447	0.387		-0.100
3.	3920		882		7056		0.388	-0.365		-0.167
4.	3920		882		7056		0.388	0.365		-0.167
5.	3920		882		7056		0.528	-0.365		-0.167
6.	3920		882		7056		0.528	0.365		-0.167

программном комплексе дополнительно реализовано вычисление собственных частот колебаний ДГУ и рамы на основе метода Якоби [7].

В качестве примера были проведены расчеты дизельгенераторной установки с двухкаскадным амортизационным креплением (Рис. 1), параметры которой приведены в таблице 1.

Для оценки динамического поведения исследуемой конструкции были построены амплитудно-частотные характеристики (АЧХ) продольных, поперечных и вертикальных пе- ремещений центров масс ДГУ и рамы в диапазоне частот внешнего воздействия от 1 Гц до 30 Гц с шагом изменения частоты 0.25 Гц. Кроме того проведен расчет также для наиболее удаленных от центров масс рамы и ДГУ точек крепления амортизаторов, так как это позволяет оценить влияние угловых перемещений элементов системы (Рис. 3). Собственные частоты колебаний рамы и ДГУ имеют следующие значения: f1=6.8 Гц, f2=10.7 Гц, f3=13.5 Гц, f4=45 9 Гц, f5=78.2 Гц, f6=73.9 Гц, f7=17.0 Гц, f8

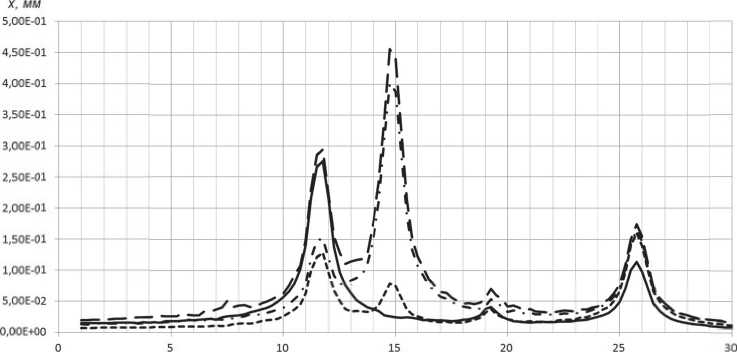
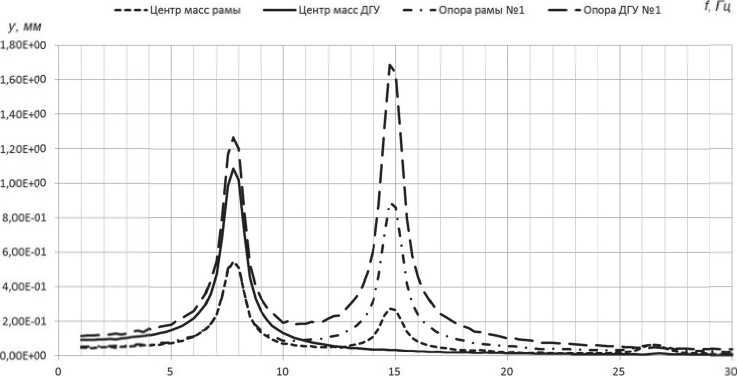
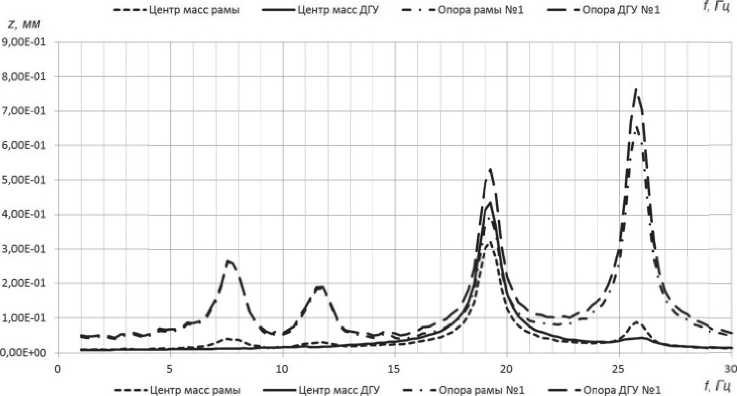
Рис. 3. Расчетные амплитудно-частотные характеристики

=23.0 Гц, f9 =22.8 Гц, f10=61,9 Гц, f11 =119.6 Гц и f12 = 128.8 Гц.

Анализ расчетных данных и графиков ам-  1.

плитудно-частотных характеристик показывает возникновение резонанса в областях собственных частот рамы и ДГУ. Приведенную конструкцию нельзя считать удачной, так как значения ₂ некоторых собственных частот попадают в ра-    ^.

бочий диапазон (для данной конструкции ДГУ рабочий диапазон составляет 15-25 Гц или 900- 3. 1500 об/мин).

ЗАКЛЮЧЕНИЕ

В заключение можно сделать следующие выводы: предложенная методика и разработанный на её основе программный комплекс _5. позволяют оценить динамические перемещения и динамическую нагруженность элементов амортизации ДГУ при различных параметрах внешнего воздействия. Кроме того, приведенный программный комплекс позволяет проанализировать влияние параметров амортизаци-   ^6.

онного крепления (количество, расположение, жесткостные характеристики амортизаторов) на динамическую нагруженность элементов с целью выявления направлений для улучшения существующих конструкций ДГУ с точки зрения 7. вибрационной защиты.