Математическое моделирование динамики процессов тепловлажностной обработки капиллярно-пористых коллоидных дискретных материалов

Одобренная Правительством РФ “Энергетическая стратегия России до 2020 г.” и принятая им 17 ноября 2001 г. Федеральная целевая программа “Энергоэффективная экономика” предусматривают в числе важных приоритетов резкое повышение эффективности использования топливно-энергетических ресурсов на основе энергосберегающих технологий и оборудования и его совершенствования.

Среди приемов энергосбережения при тепловой сушке малоизученным аспектом является энергосбережение за счет снижения технологического брака. Рассматривая эту проблему на примере таких дискретных материалов лесной промышленности, как пиломатериалы, или промышленности строительных материалов, как кирпичи, можно предполагать, что снижение технологического брака, достигающего в этих отраслях промышленности величин 5 – 30 %, за счет рационального управления кинетикой сушки дискретного материала в различных точках поперечного сечения сушильных камер позволит снизить не только прямые затраты энергии на сушку, но и вспомогательные – на транспорт, рубку, распиловку исходного сырья. Выполнен

ный нами анализ позволяет в масштабах страны оценить возможную экономию энергии только при сушке пиломатериалов в 1,5 – 1,8 млн тонн условного топлива.

Для разработки методов инженерного расчета и создания современных энергоэффективных сушильных установок необходима информация о процессах, развивающихся в их элементах, что невозможно без проведения широкомасштабных исследований. Нередко такая информация по своему объему недостаточна и требуется принятие конкретных технических решений в условиях неопределенности. Тогда наряду с проведением комплексных экспериментальных исследований гидродинамического совершенства существующих рабочих камер и технологических процессов как в промышленных, так и лабораторных условиях [1,2], также особенно эффективно применение методов математического моделирования сушильных и смежных процессов с помощью вычислительной техники.

В исследовании нестационарных полей влагосодержания и температуры в работе использовалась известная математическая модель, базирующаяся на системе нелинейных дифференциальных уравнений для нестационарного внутреннего влаго- и теплопереноса при сушке влажных тел:

_   d t    д (.д t )           д®

Cpo    =I Д 1 + e" r' Po дт dx ( дx )           дт д® дт

д (   д®     _ed t ।

I a m      + a m o-     I ,

дx (   дx       дx J

где am, λ, δ – соответственно коэффициенты потенциалопроводности, теплопроводности и термоградиентный коэффициент; С, r, ε – удельная теплоемкость, теплота фазового перехода и критерий фазового превращения [3].

Универсальные граничные условия, предложенные в математической модели поверхностного испарения [4,5,6], учитывают снижение действительной движущей силы внешнего массо-переноса за счет изменения поверхностного влагосодержания и интенсивность испарения. Мо- дель поверхностного испарения описывает непрерывно в первом и втором периодах сушки весь процесс как в жестких, так и мягких условиях сушки.

Использование подобной модели в вычислительном эксперименте предполагается перспективным, поскольку в условиях непрерывного изменения входных условий в сушилке (различные виды пород, изменение структуры, начального влагосодержания и т.д.) только расчет на ЭВМ позволяет контролировать состояние материала на выходе из сушильной камеры и управлять процессом сушки по заданным в первую очередь критериям качества сушильного материала.

При конвективной сушке капиллярно-пористого тела в форме пластины граничные условия

можно записать в виде + , д t ± ^“ - аУ- » - t»)+ Pp ■ Дп (Pw - P»)' r(1 - e)= 0,                      (3) (д®    дt)          /        \ ± am Po K- + 0T- I-Pp ■ Дп (Pw - P») = 0.                      (4) ( дx    дx J Начальные условия: t (.) = to = f (.); ®(x) = ®o = f (x),                               (5) где βp, α, ρо – соответственно коэффициенты массообмена и теплоотдачи, начальная плотность; Дп – критерий поверхностного испарения, определяемый по отношению действительного перепада движущей силы внешнего массопереноса к максимально возможному.

Критерий Д учитывает не только реальные свойства конкретного материала, но и факторы,

п влияющие на массоперенос, такие как характерный размер пор, пористость материала.

Критерий поверхностного испарения учитывает также реальные свойства конкретного ма- териала:

Дп =

R f + 1 + P w /P’

где Pw – парциальное давление пара у поверхности мениска; Р – полное давление в сушильном агенте; Rf – критерий интенсивности испарения, представляющий собой отношение диффузионных сопротивлений пограничного слоя и устьев капилляров с учетом действительного проходного сечения для пара.

Критерий интенсивности испарения учитывает также факторы, влияющие на массоперенос, такие как характерный размер пор, пористость материала П :

Rf Цю- П / Юм )2/3, где ωм – влагосодержание намокания. м

При разработке уточненной методики расчета неравномерного тепломассообмена диффе- ренциальные уравнения тепло- и массопереноса рассматриваются для системы капиллярнопористое тело – связанное вещество, которая в области положительных температур (t > 0 оС) может быть в виде жидкости, пара и инертного газа. Часть капилляров в этих условиях заполнена жидкостью, а остальная часть – парогазовой смесью, если не учитывать влияние отрицательных температур.

Для обычных условий давление влажного воздуха близко к барометрическому, и масса воздуха и пара в капиллярах по сравнению с массой жидкости ничтожно мала. Поэтому в области положительных температур с большой степенью точности удельное влагосодержание тела можно считать равным удельному влагосодержанию жидкости, и если отмечать парообразную влагу индексом 1, а жидкость – 2, то ω = ω ₂.

Жидкость в пористом теле в общем случае может перемещаться путем избирательной диффузии через скелет тела (молекулярный перенос) в виде фильтрационного движения под действием силы тяжести или гидростатического давления (молекулярный или конвективный перенос), а также путем капиллярного впитывания.

Как термодинамические характеристики, так и коэффициенты влаго- и теплопереноса ( а_m , λ , δ ) зависят от влагосодержания и температуры, а также от вида материала. Поэтому использование в широких диапазонах изменение характеристик материала отмеченной выше системы уравнений затруднено отсутствием кинетических коэффициентов.

Коэффициенты аm и δ, если направление векторов диффузионных потоков пара и жидкости одинаково, соответственно равны:

a

m

= m1

_s a m, 5 1 ⁺ a m, 5 2

+ am,; 5 = —-----—

^{2          a}m, ^{+ a}m

.

Термоградиентный коэффициент δ определяется экспериментально как отношение гради- ента влагосодержания к градиенту температуры в отсутствие массопереноса, поэтому в гигроскопической области δ1 = δ2. Можно описать и перенос пара и жидкости в гигроскопической области через единый градиент потенциала массопереноса θ. Если пренебречь эффектом Соре (термодиффузия пара и растворенного вещества в жидкости), то можно написать:

^^-

j =-^m ™, где λm – коэффициент пропорциональности между плотностью потока влаги jm и градиентом потенциала ∇θ называется коэффициентом массопроводности по аналогии с коэффициентом теплопроводности X, равным X = jq/ V/.

Коэффициент а_m является аналогом коэффициента температуропроводности а_р :

a

m

^^■а

; ap cmY

X cpY ’

где γ – плотность скелета пористого тела.

Данная аналогия обусловила в работах [3,7] название коэффициента аm как коэффициента потенциалопроводности массопереноса, поскольку коэффициент температуропроводности ар можно назвать коэффициентом потенциалопроводности теплопереноса. При интенсивном нагреве влажного тела также возникает градиент общего давления за счет испарения жидкости при температуре ≥ 100 оС.

Для различных температурных режимов зависимость коэффициента потенциалопровод- ности аm и термоградиентного коэффициента δ для такого коллоидного капиллярно-пористого тела, как, например, сосна, представлены на рис. 1.

Для повышения достоверности проектирования конвективных сушильных установок необходимы углубленные исследования по влиянию различных факторов на интенсивность внешнего теплообмена. Отрывочные и противоречивые опытные данные (В.В. Смагин, Р.Ш. Вайнберг, Б.Ф. Бояршинов, О.Л. Данилов) по влиянию поровой структуры сушимого материала и физических свойств испаряемой жидкости, а также существенные отличия в значениях коэффициен- тов теплоотдачи при испарении из капиллярно-пористых тел и при вдуве в пограничный слой инертного газа вызывают необходимость более детального изучения физики происходящих при этом процессов.

Опытные исследования выполнялись на специально разработанном стенде, в качестве испаряемых жидкостей использовались вода, этиловый спирт и ацетон как теплоносители, имею-

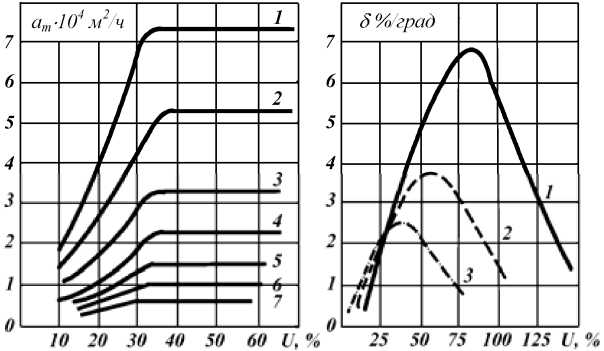
Рис.1. Зависимость коэффициента потенциало-проводности а_m (1 – 100 ^оС; 2 – 90 ^оС; 3 – 80 ^оС; 4 – 70 ^оС; 5 – 60 ^оС; 6 – 50 ^оС; 7 – 40 ^оС) и термоградиентного коэффициента δ (1 – 40 ^оС; 2 – 70 ^оС; 3 – 100 ^оС) от влагосодержания древесины (сосна)

щие различную, например, температуру кипения, теплоту фазов измерении осредненных характеристик динамического и теплово не пластины с различной пористой структурой (керамика, порол ные хромель-копелевые термопары и щелевой насадок полного метр. Температура основного потока при безградиентном течени t = 20 ^ 140 оС, число Re = 3,5-105, степень турбулентности 8 = 3,5 %.

По результатам измерения осредненных характеристик оп тров, в частности интенсивность испарения, кг/м2-ч, по соотношению:

qм = ^(tп - tмт 1                                  СИ)

r где r – теплота фазового перехода, кДж/кг; tп и tмт – соответственно температура ядра нагретого потока и температура мокрого термометра.

Коэффициент теплоотдачи, Вт/м2-К, определялся на основании измеренного температурно- го градиента:

а = - Я

(d t / Oy) w (t п - tмт ) ,

где X - теплопроводность, Вт/м - К; ( д t/ д y ) - градиент температуры у стенки, К/м. ^w

При этом интенсивность теплообмена, кДж/м2-ч, определяется как qw = qм • r •

Разброс опытных данных при проведении экспериментов составил до ± 8 %. Проведенные исследования подтверд иянии на локальные коэффициенты отмеченных выш тное влияние пористость материалов на коэффициент д р различных жидкостей оказывает при высоких температурах, что наглядно продемонстрировано на рис. 2а.

Величина теплового потока к поверхности при испарении воды и варьировании пористостью и температурным напором изменяется и по длине капиллярно-пористого материала. Величина коэффициента теплоотдачи (рис. 2б) снижается довольно значительно при уменьшении пори ст ости, причем с ростом температурного напора эта разница увеличивается. Так, при уменьшении пористости до П = 0,8 величина а снижается на 20 %, а при П = 0,17 - более чем в два раза.

В исследуемом температурном диапазоне температура мокрого термометра у этилового спирта в среднем на 9 ^ 11 ^оС ниже, чем у воды, а у ацетона, соответственно, на 23 ^ 25 ^оС.

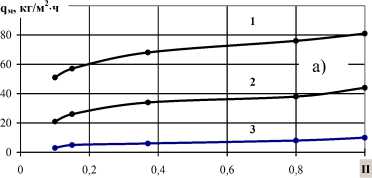
Рис. 2. а – влияние пористости материала на интенсивность испарения при температуре 100 ^оС различных жидкостей: 1 - ацетона; 2 - спирта; 3 - воды. б - Влияние пористости П и температурного фактора A t на коэффициент теплоотдачи а при испарении воды

Ориентировочно эти пропорции соблюдаются и при изменении коэффициентов теплоотдачи в зависимости от физических свойств исследуемых жидкостей. Опытные данные по интенсивности испарения и коэффициентам теплоотдачи могут служить тестом при оценке корректности математических моделей по отношению к реальному физическому процессу для отмеченных выше условий.

Алгоритм решения нелинейной краевой задачи влаго- и теплопереноса в капиллярнопористых телах (уравнения 1-5) реализован программно на языке Pascal [8]. Для температурных режимов, пористости, коэффициентов влаго- и теплопереноса и термодинамических характеристик пористых материалов, использованных при экспериментальном исследовании процессов испарения, выполнено тестирование разработанной программы «Fields». Для обработки выходных данных (количество численных значений более 40000) разработана программа «Picture», позволяющая представлять интегральные и текущие числовые данные в виде графиков в размерных координатах.

Результаты расчета процесса сушки различных пород древесины (сосна – рис. 3, береза – рис. 4) удовлетворительно согласуются с опытными данными работы (Г.С. Шубин) и располагаются в диапазоне изменения влагосодержания материала вследствие изменения пористости (темный фон) в соответствующих временных интервалах продолжительности сушки.

Расчет процесса сушки сосны толщиной 25 мм выполнен при условиях: ω _н = 30 %, ω _к = 5 %, t_с = 70 ^оС. При изменении пористости материала с 0,1 до 0,5 (рис. 3а) продолжительность процесса сушки уменьшается на 12-13 %. Эволюция полей влагосодержаний и температур представлена на рис. 5.

Неучет влияния пористости (в диапазоне 0,1 и 0,5) приводит к увеличению продолжительности сушки березы на 18-19 % (толщина 20 мм, ω _н = 100 %, ω _к = 12 %, t_с = 50 ^оС).

Для температурных режимов, пористости, коэффициентов влаго- и теплопереноса и термодинамических характеристик пористых материалов, использованных при экспериментальном исследовании процессов испарения, выполнено тестирование разработанной программы «Fields». Расчетные кривые по интенсивности испарения воды с пористой поверхности достаточно хорошо согласуются с экспериментальными данными, что позволяет сделать вывод о применимости

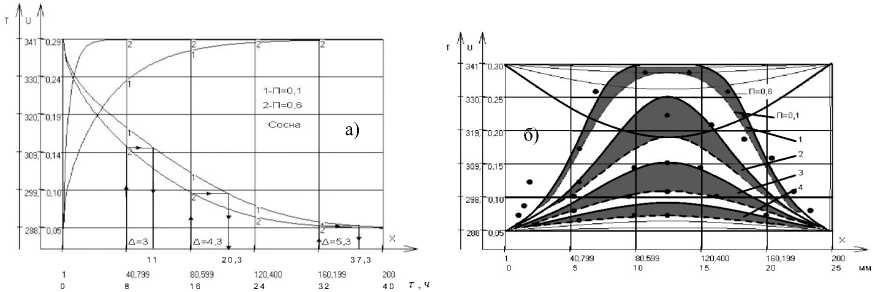
Рис. 3. Кривые сушки сосны толщиной 25 мм при изменении пористости (а) и совмещенные кривые распределения влаги в древесине (б) при пористости 0,1 и 0,5 при сушке сосны в интервалах по времени: 1-8; 2-16; 3-24; 4-32 часа. Точки – эксперимент (Г.С.Шубин)

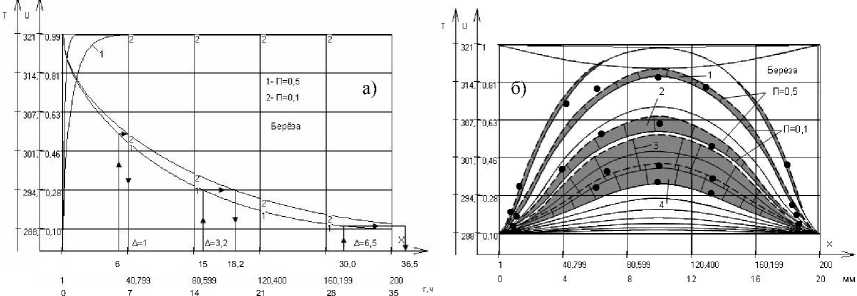
Рис. 4. Кривые сушки березы толщиной 20 мм при изменении пористости (а) и совмещенные кривые распределения влаги в древесине (б) при пористости 0,1 и 0,5 при сушке березы в интервалах по времени: 1-7; 2-15; 3-30; 4-37 часов. Точки – эксперимент (Г.С.Шубин)

данной методики расчета при различных граничных условиях к расчету интенсивности процессов испарения капиллярно-пористых структур.