Математическое моделирование динамики системы с N телами, закрепленными на двух упругих стержнях

Настоящая работа посвящена дальнейшему развитию исследований, начатых в публикациях [1–4], в области математического моделирования динамики механических систем, включающих упругие элементы и закреплённые на них тела.

Ранее в работе [1] была представлена обобщённая математическая модель для систем с одним упругим стержнем, а также разработан универсальный подход к анализу свободных колебаний этого класса моделей [2]. В данном исследовании предложенный подход развивается путём перехода от системы с одним стержнем к системе с двумя стержнями, что расширяет возможности моделирования более широкого спектра механических систем. В работах [3–4] рассматривались случаи с одним и тремя телами. Это исследование обобщает полученные ранее резуль- таты на систему, состоящую из (n) тел, закреплённых пружинами на двух горизонтальных упругих стержнях.

Для получения уравнений движения применён вариационный принцип Гамильтона — Остроградского, который обеспечивает гибкость и точность в учёте связей между телами и стержнями. Итоговая система уравнений относится к классу гибридных систем дифференциальных уравнений, комбинирующих обыкновенные дифференциальные уравнения и уравнения в частных производных, что требует использования специализированных методов решения.

Новизна исследования заключается в изучении системы с креплением тел на двух упругих стержнях, что ранее не рассматривалось в рамках данного подхода. Разработанная модель позволяет анализировать дополнительные факторы взаимодействия и расширяет возможности исследования динамических характеристик сложных конструкций.

Такие модели находят применение в проектировании высокоточных динамических систем, а также в исследованиях по управлению и оптимизации сложных механических конструкций, включая микроэлектромеханические системы (MEMS), робототехнические устройства и другие инженерные структуры.

1 Постановка задачи

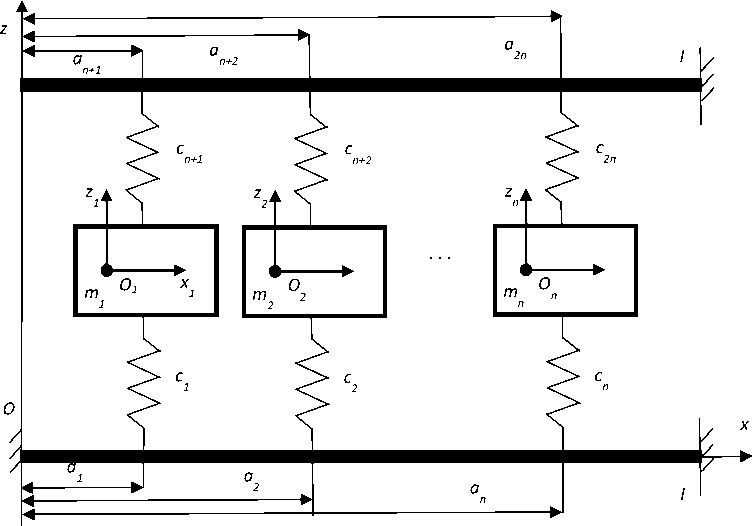
Рис. 1. Механическая система из n тел, закрепленных на двух упругих стержнях

Рассмотрим механическую систему (рис. 1), состоящую из n горизонтально расположенных тел, закреплённых пружинами между двух упругих стержней. Концы стержней жестко закреплены. В качестве модели упруго стержня рассматривается балка Эйлера — Бернулли.

Задача состоит в построении математической модели, описывающей малые поперечные колебания такой системы, с учётом упругих свойств стержней, инерционных характеристик тел и условий взаимодействия между телами и стержнями.

2 Математическая модель

Обозначим прогибы стержней в точке x в момент времени t функциями u₁ (x, t), u₂ (x,t) . Так как тела совершают поступательные движения только в направлении оси Oz и могут совершать угловые отклонения р_г, i = 1,2 ...п перемещения точек тел с координатами x , z будут иметь вид:

z = zm,+ ^Z' + x'^ ,                                           (1)

где z_{m i} ( t ) — перемещения центров масс твердых тел.

Вследствие этого координаты точек крепления пружин к твердым телам будут иметь вид:

^Z i , j = z _mi + ^Z ' +n ⁺ di + j^n ^ n , i = ¹•• ^{n ,} J = { 0,1 } ,                           ⁽²⁾

где за координату X принимается отклонение точки крепления пружины от центра масс тела по оси Ох, и для удобства обозначим ее как d_i , где i — номер пружины. А Z' — отклонение от центра масс по оси Oz точки крепления пружины номер i. При j = 0 соотношение (2) описывает координаты точек крепления пружин, прикрепленных к нижнему стержню, а при j = 1 — к верхнему.

Составим интеграл действия по Гамильтону. Для рассматриваемой системы он будет иметь следующий вид:

t ₁

j 6(Т - U) dt = 0,(3)

t ₀

где T и U — кинетическая и потенциальная энергии системы и для них справедливо следующее уравнение:

2n и = y U + Uc, T= У T + T(4)

i=1

где:

2 n

У U i — сумма потенциальных энергии пружин;

i = 1

U _c — сумма потенциальных энергии стержней;

n

Ут— i=1

сумма кинетических энергии тел;

Т с — сумма кинетических энергии стержней.

Запишем соотношения для U_i с учетом соотношения (2)

U i =

c i ⁽ z m - ^z ‘ + ^di P i ^{— U} 1 ⁽ a i , t ^{)) 2} + c n + i ⁽ z m + ^Z + + d n+i Pj ^— u 2 ⁽ a n+i , t))²

где сi

— коэффициенты упругости пружин.

, i = 1..n , (5)

Кинетические энергии T_i имеют вид:

T =

mz I p i mi p

---- + ——, i = 1.. n

22    ^,

где m, — массы тел, а I

I                                        р/

момент инерции тела относительно оси, проходя-

щей через его центр масс при угловых отклонениях р .

Энергия стержней в соответствии с моделью балки Эйлера-Бернулли будет иметь следующий вид:

l

T = ?(/

l

du1 dt

l

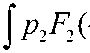
2 l du. , 2 dx + j e ₂ i ₂< dx ₀

^{du 2} ) ² dx ), dt

^{d 2 u 2} ) ² dx ) dx ²

,

где pF — линейная плотность массы, a EI - изгибная жёсткость.

Перепишем интеграл действия по Гамильтону с учётом соотношений для потенциальной и кинетической энергий (4) — (7)

t ₁

n

J=12

2 mz m ₊

^ ci^(zi,0 “ ^u 1 ( a i ^,t))2 c n + ( z ij ^— Щ^п+^ У)

t ₀

t ₁

+

i = 1

V 2     2

12 Y

- di ⁺

)_

(д ²   , T .

—- u. (x,t) dx dt +

t1 1        ( д                  1c

J 2JP1F1 lau1(x,t)ldx“^EI1

0       V ^tl         J 0

l

l

t ₀

+

V

J

Jd            д

dt .

t ₀

Заметим, что функционал действия зависит от перемещений центров масс тел z_m . , угловых отклонений тел

j, а также от прогибов нижнего и верхнего стержней и₁,и₂-

Запишем вариацию для центров масс z_m. при i 6 [1,п]: t1

^ ^J- = J( mzm “ ci[ Z-0 “ ^u1 ( ai ’ t )]“ cn+i^[z* “ u2 ( an+i ’ t )])^Jzmdt ’ ⁽⁸⁾ t₀

Вариация для угловых отклонений тел р^ при i 6 [1, п]:

t₁

J =f( I^^Pi - cd^[zifi - u1 ( ai^,t)]-cn-dn-z - u2 ( an+i ’t)])⁵P^dt• ⁽⁹⁾ t₀

Вариация для прогибов нижнего и верхнего стержней и₁, и₂.

#J u1

t11 f

= П cl [ ^1 to ⁰^

- U1 ( x, t)

- PF1

d²u1

It^ —

E1I1

d 4Ui^ dx⁴

5u1dxdt

^t1 l

^JU2 =П ^t0 ⁰

c4

I

u z6

-

^U2 (^x, t) ^-PF2

d 2u2 dt2

F I

E₂I₂

54U2 ] dx⁴ ^

5u2dxdt

Применим основную лемму вариационного исчисления к 8–10 и получим искомую математическую модель в виде гибридной системы дифференциальных уравнений.

mizm,^-ci [ zi,0 ^{- u}i ( ^ai■, t )] ^-cn+i [ zi1^{- u}2 ( an+i■^,t)] = ⁰’ i = 1..n;

Ip,8-cidi [ z’0 - ui ( ai’ t )]-cn+idn+i [ z,1 - u2 ( an+i’ t )] = 0’ i = 1-n

* P^F1      ^{+ EI}      = ^ci [zi-0 ^{- u}1 (^x,t)^{] 5} (x^-ai )

Ct           Oxi

P^F2     ^{+ E}2I^{1 du2}= ^^^[z^ - ^u2 (x’t)^{] 5} (x - an+i )•

Gt            dxi где на функции и^х, t), и2(х, t) в силу способа закрепления стержней действуют следующие граничные условия:

и₁(0, t) = и₁(1. t) = 0, U2 (0, t) = и₂ (I, t) = 0, ^^(0,О = ^^(_г,г) = 0’ ^d-^(0,t)=^d-^(l,t) = 0. U Л л

Заключение

В статье разработана математическая модель, описывающая динамику механической системы из (n) твёрдых тел, закреплённых на двух упругих стержнях. Модель учитывает поступательное и вращательное движение тел, а также поперечные колебания стержней, описываемые в рамках теории балки Эйлера– Бернулли. Уравнения движения получены с применением вариационного подхода, основанного на принципе Гамильтона — Остроградского. В результате получена гибридная система дифференциальных уравнений. Данная модель может быть использована в дальнейшем при уточнении обобщенной модели на случай крепления тел между двух упругих стержней.