Математическое моделирование динамики транспорта О2 в эритроцитах и плазме крови в капилляре

Разработка аналитических методов и приборов для исследования процессов газообмена в системе микроциркуляции органов и тканей является определяющим фактором успешного развития ряда важных направлений современной физиологии и медицины. Это обусловлено тем, что одним из главных условий нормального функционирования большинства организмов является адекватное потребностям обеспечение клеток их органов и тканей энергией, получаемой внутриклеточными системами аэробного энергетического метаболизма в ходе реакций, идущих с участием кислорода [1]. Поэтому возникающий дефицит кислорода, например понижение его содержания в клетках коры головного мозга до критического уровня (1–3 мм Hg) в результате прекращения поступления с током крови, уже через 2–3 с приводит к потере сознания, а через несколько минут — к необратимому нарушению структуры и функции клеток вплоть до их гибели. Соответствие доставки кислорода к клеткам меняющейся во времени их потребности в нем обеспечивается главным образом эффективностью пространственной организации и функционирования транспортных систем микрицирку-ляторного уровня. В наибольшей степени она зависит от геометрии капилляров, размеров, формы и числа эритроцитов в единице объема крови, скорости движения эритроцитов и плазмы крови по микрососудам, скорости диффузии О2 в ткани, статических и динамических показателей кисло-родсвязывающих свойств крови. В реальных условиях большинство этих параметров под влиянием разнообразных естественных, экстремальных и патологических факторов подвержены быстрым изменениям, что отражается на обеспечении тканей кислородом. Достаточно отметить, что амплитуда колебаний скорости кровотока в микрососудах — одного из ведущих транспортных механизмов в системе микроциркуляции — варьирует в пределах 0,5–100 % от ее средних значений, а их период изменяется от долей секунды до нескольких секунд [2, 3]. Этот интервал времени сопоставим с продолжительностью процессов диссоциации оксигемоглобина (HbО2) в клетках крови [4], являющейся важнейшей динамической характеристикой массопереноса кислорода в капиллярах, а также с длительностью процесса диффузии О2 в межкапиллярном пространстве [5] и пребывания эритроцита в капилляре [6]. Поэтому изучение динамики транспорта О2 в эритроцитах и плазме капилляров, выяснение ее значимости в процессах массопереноса О2 в межкапиллярном пространстве тканей являются актуальной проблемой для физиологических и медицинских исследований, связанных с анализом механизмов обеспечения нормальной деятельности клеток, ее нарушений и коррекции. Однако проведение таких тончайших экспериментальных исследований сталкивается со значительными методическими трудностями, которые обусловлены сложностью пространственно-временнόй организации анализируемых процессов и отсутствием надежных теоретических представлений о транспорте О2 в системе микроциркуляции.

Для решения этой проблемы предлагается использовать возможности методов математического моделирования, достоинства которых показаны, в частности, при исследовании условий транспорта О2 в капиллярах в статике [7, 8, 9, 10]. Как правило, кровь в этих моделях представлена в виде гомогенной среды, а ее кислородсвязывающие свойства описаны кислородной емкостью и кривыми диссоциации оксигемоглобина, что является достаточным для приближенной оценки процессов массопереноса в системе микроциркуляции. Более детальное исследование механизмов кислородного обеспечения тканей выполнено на моделях, имитирующих пространственное распределение О2 в отдельных эритроцитах [11, 12]. Однако для анализа реальной динамической картины действия взаимосвязанных кислородтранспортных механизмов в микроучастках тканей такое приближение недостаточно. Поэтому для изучения динамики процессов транспорта кислорода была разработана модель ячейки капиллярной сети, учитываю-шая диффузию О2 и кинетику диссоциации оксигемоглобина в эритроците дискоидальной формы [13]. Целью настоящей работы явилось дальнейшее совершенствование этой модели (позволяющее учитывать измерения таких важных факторов, влияющих на кислородтранспортные свойства крови, как форма эритроцита и диффузия оксигемоглобина в теле этой клетки) и ее применение для анализа динамики массопереноса О2 в капиллярах.

ОПИСАНИЕ МОДЕЛИ

Анализируется транспорт О 2 в пространстве цилиндрического капилляра радиусом r c , по которому на равном расстоянии l c со скоростью v движутся эритроциты, одинаковых размеров и формы (рис. 1). Известно, что в зависимости от гемодинамических условий (скорости кровотока и вязкости плазмы) и механических свойств цитоплазмы и клеточной мембраны эритроцит может менять свою форму [12]. Учитывая наблюдаемые в экспериментах изменения формы клеток крови в капиллярах, в модели для малых величин v рассматриваются эритроциты обычной дискоидальной формы радиусом r e и толщиной h (рис. 1, а), а для средних и больших v — клетки пулеобразной формы (рис. 1, б), имеющие равные объемы и площади поверхности. Поскольку в нормальных физиологических условиях расположение клеток и плазмы крови в капиллярах является регулярным, рассматривается перенос О 2 в некоторой ячейке, включающей сегмент капилляра, заполненный плазмой с эритроцитом в его центральной части. При этом считается, что эритроцит и окружающая его плазма движутся по капилляру с одинаковой скоростью.

Рис. 1. Схематическое изображение ячейки в виде сегмента капилляра с эритроцитами диско- (а) и пулеобразной (б) формы

Эритроцит в модели представлен в виде трехкомпонентной среды — цитоплазмы, в которой О 2 находится в растворенном состоянии, гемоглобина и оксигемоглобина, в котором О 2 находится в связанном состоянии. Рассматривается сегмент капилляра, в котором кислород, растворенный во внутриклеточном пространстве и плазме крови, переносится путем диффузии по градиенту его концентраций. Поэтому изменение во времени t его парциального давления или напряжения ( р О₂) в пространстве ячейки в радиальном ( r ) и осевом ( X ) направлениях Up ( r,x,t ) описывается уравнением диффузии, которое в цилиндрических координатах имеет вид

U _ D^ д t      ( д r ²

+ 1 д Up +

r d r

^p Y m , д x ^{2 J} a i

где a i ( r , x ) и D i ( r , x ) — коэффициенты растворимости и диффузии О 2 в плазме вне ( α_p и D_p ) и внутри ( α_e и D_e ) эритроцита, m ( r, x, t ) — скорость поступления О 2 в плазму эритроцита в результате рассыщения оксигемоглобина.

Считается, что m пропорционально градиенту парциального давления k , при котором осуществляется рассыщение HbO 2 ( Ug ) и давления О 2 , растворенного в цитоплазме эритроцита ( Ue ) (которое равно Up в пределах границ эритроцита) [13]:

m = k [ Ug ( r , x , t ) - Ue ( r , x , t )] .

Парциальное давление Ug зависит от количества О2 , связанного гемоглобином, и определяется по кривой диссоциации оксигемоглобина [14]. В этом случае уравнение, описывающее изменение во времени концентрации О2, связанного гемоглобином (Сg (r, x, t)), в процессе рассыщения и диффузии оксигемоглобина в эритроците по гра- диенту его концентрации имеет вид

?a=Dg (Ca++1 deg+UC.)_ m, dt       ^ dr2    r dr     9x2 J ai- где Dg (r, x) — коэффициент диффузии оксигемоглобина в цитоплазме эритроцита.

Парциальное давление О 2 на поверхности капилляра принимается постоянным и близким к его среднетканевым значениям в коре головного мозга — 20 мм Hg [15]. Считается, что на торцах ячейки, на ее левой (G 1 ) и правой (G 2 ) границах (рис. 1) ввиду равномерного распределения эритроцитов в капилляре градиенты напряжений О₂ в плазме крови в осевом направлении равны:

d Up _ д Up д t|G|     д r|c 2

Решение приведенной системы уравнений осуществлялось на ЭВМ численным методом конечных разностей. Для этого непрерывная область изменения независимых переменных ( r , x , t ) заменялась расчетной сеткой с равномерными шагами по этим переменным. В узлах сетки исходные дифференциальные уравнения аппроксимировались явными разностными уравнениями с точностью до второго порядка. При этом величины шагов сетки подбирались с учетом устойчивости линейной разностной задачи. Затем по начальным значениям искомых переменных последовательно с заданным шагом по времени рассчитывались их текущие величины.

В начальный момент времени р О 2 в цитоплазме эритроцита и плазме крови равно его значениям в плазме артериальной крови — 94 мм Нg [16]. Максимальная внутриклеточная концентрация О 2 ,

Численные значения величин, принятые в модели [13]

α p	Растворимость О2 в плазме крови	9,4 10 - 10	мол/см3 мм Hg
α e	Растворимость О 2 в цитоплазме эритроцита	1,56 10 - 9	мол/см3 мм Hg
D p	Коэффициент диффузии О 2 в плазме крови	1,65 10 - 5	см2/с
D e	Коэффициент диффузии О 2 в цитоплазме эритроцита*	9,5 10 - 6	см2/с
D g	Коэффициент диффузии HbO 2 в эритроците**	7,04 10 - 7	см2/с
k	Коэффициент, характеризующий кинетику дезоксигенации HbO 2	0,005	см3О 2 /см3 с мм Hg
r e	Радиус эритроцита	4,2	мкм
h e	Толщина эритроцита	2,0	мкм
r c	Радиус капилляра	10	мкм
l c	Длина сегмента капилляра	10	мкм

— по данным [9], ** — по данным [19].

связанного гемоглобином, исходя из средней величины гематокрита 40 % и кислородной емкости крови 0,2 (мл О 2 )/(мл крови) [17], считается равной 0,5 мл О 2 /см³. При р О 2 = 94 мм Hg, согласно расчетам по кривой диссоциации оксигемоглобина [14], Сg = 0,47 мл О 2 /см³. Шаг сетки в осевом и радиальном направлениях составлял 0,5 мкм, а шаг по времени — 0,00001 с, что обеспечивало приемлемые точность и продолжительность расчетов. Численные значения коэффициентов, принятые в модели, представлены в таблице.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

На модели было рассчитано изменение во времени основных параметров, характеризующих условия транспорта О2 в микрососудах: распределения напряжений О2 в цитоплазме эритроцита (Ue) и плазме крови в капилляре (Up), а также парциального давления О2 , при котором осуществляется рассыщение HbО2 (Ug) и концентрации О2, связанного гемоглобином (Cg), в эритроците при его движении по капилляру от артериального конца к венозному. Полученные данные показали, что в артериальной части капилляра уже в начальный момент рассыщения оксигемоглобина (через 0,006 с нахождения дискоидального эритроцита в капилляре) в плазме крови устанавливается неравномерное распределение рО2 (рис. 2, а). Его наибольшие значения 55,5 мм Hg отмечаются в центральной части ячейки, в месте нахождения эритроцита. Уровень рО2 плавно уменьшается в осевом и радиальном направлениях, достигая на левой и правой границах ячейки 44, а вблизи поверхности капилляра 23–25 мм Hg. Характер распределения рО2 в плазме крови в капилляре в определенной степени зависит от формы эритроцита. Так, в центре ячейки с эритроцитом дискоидальной формы область с повышенным рО2 в плазме крови вытянута в радиальном направлении. В отличие от этого в ячейке с пулеобразным эритроцитом область с повышенным рО2 вытянута в осевом направлении (рис. 2, б). Кроме того, максимальные значения рО2 в центральной части ячейки с пулеобразным эритроцитом и на ее торцах примерно на 10 %

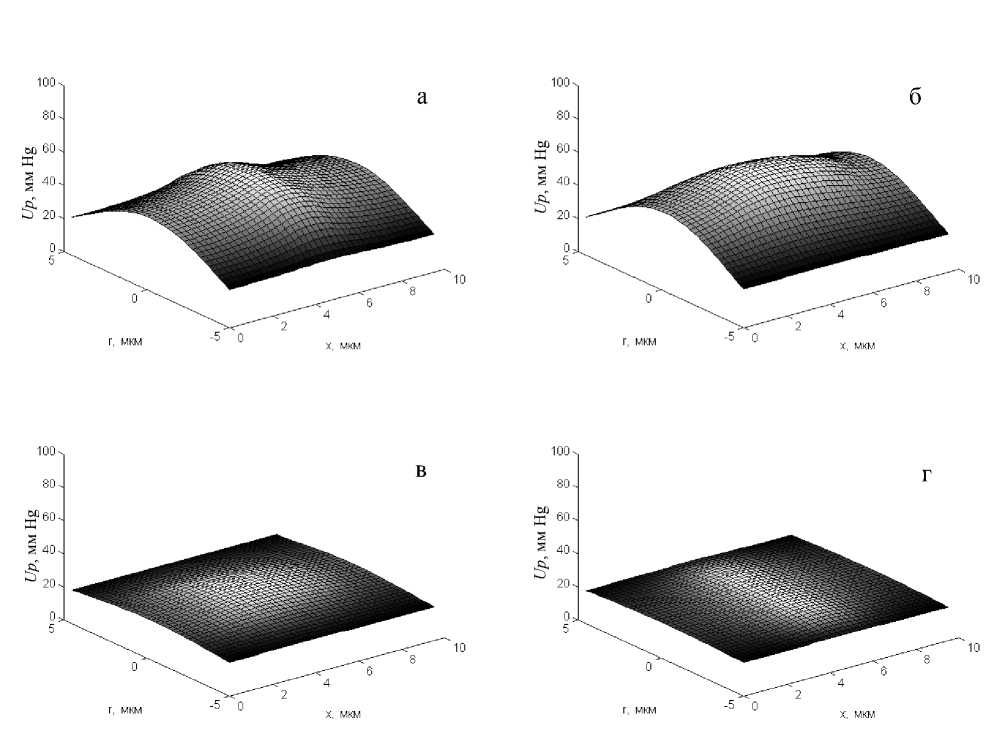
Рис. 2. Распределение рО2 во вне- и внутриклеточной плазме крови в сегменте капилляра дискообразной (а,

в) и пулеобразной (б, г) форм в артериальной (а, б) и венозной (в, г) частях капилляра

выше, чем в ячейке с дискоидальным эритроцитом. Некоторые отличия имеют и градиенты р О 2 в радиальном направлении вблизи поверхности капилляра. В центральной части ячейки с эритроцитом дискоидальной формы они примерно на 30% выше, а на торцах (G1 и G2) на 10% ниже, чем в ячейке с эритроцитом пулеобразной формы. Из этих данных следует, что эритроцит дискоидаль-ной формы при прохождении по капилляру отдает значительное количество О₂ в окружающее пространство в узкой зоне, прилежащей к его поверхности и приближенной к поверхности капилляра. В то же время в случае перемещения по капилляру эритроцита пулеобразной формы отдача О 2 эритроцитом в окружающее пространство осуществляется более равномерно по всей поверхности капилляра.

Через 0,6 с пребывания эритроцита в капилляре (что соответствует его нахождению в венозной части микрососуда) уровни рО2 в плазме крови резко уменьшаются (рис. 2, в, г). Так, наибольшие значения рО2 в центре дискоидального эритроцита составляют 25,8, а пулеобразного — 28,9 мм Hg. На оси торцевых плоскостей (G1 и G2) капилляра они равны 21,7 и 23,9 мм Hg соответственно. При этом отмечается сходство общей картины распределения уровней рО2 в плазме крови на артериальном и венозном участках капилляра.

Отмеченные профили распределения р О 2 в пространстве капиллярной ячейки во многом определяются особенностями распределения р О 2 в цитоплазме эритроцита. Согласно полученным данным, в артериальной части капилляра в начальный момент рассыщения оксигемоглобина в эритроците дискоидальной формы уровень р О 2 в его цитоплазме в радиальном направлении уменьшается на 18,7 мм Hg — от 55,5 в центре до 36,8 мм Hg на поверхности клетки (рис. 3, а). В отличие от этого в цитоплазме эритроцита пулеобразной формы, находящегося в артериальной части капилляра, отмечены менее выраженные изменения р О₂ — от 59,9 мм Hg в центре до 48,0 мм Hg на его поверхности (рис. 3, б). Тем не менее при нахождении эритроцита в венозной части капилляра независимо от формы клетки в ее цитоплазме устанавливается более равномерное распределение р О 2 . Так, в эритроците дискоидаль-ной формы р О 2 в цитоплазме в радиальном направлении уменьшается на 2,5 мм Hg — от 25,8 в его центральной части до 23,3 мм Hg на его

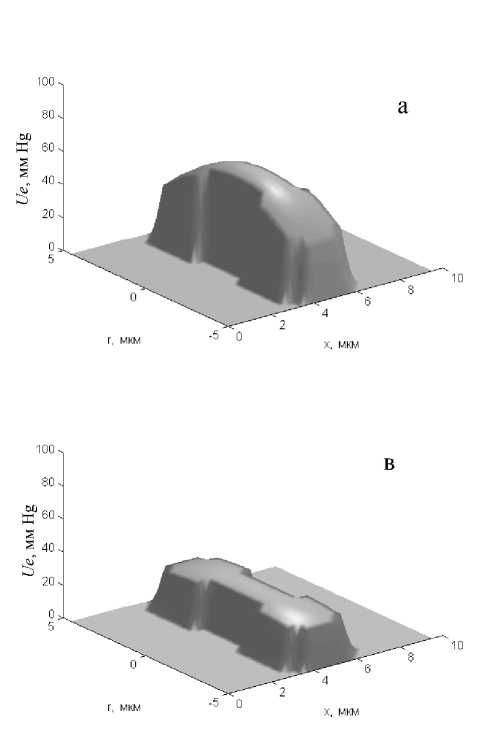
Рис. 3. Распределение р О₂ вблизи наружной поверхности и в цитоплазме эритроцита дискообразной (а, в) и пулеобразной (б, г) форм в артериальной (а, б) и венозной (в, г) частях капилляра

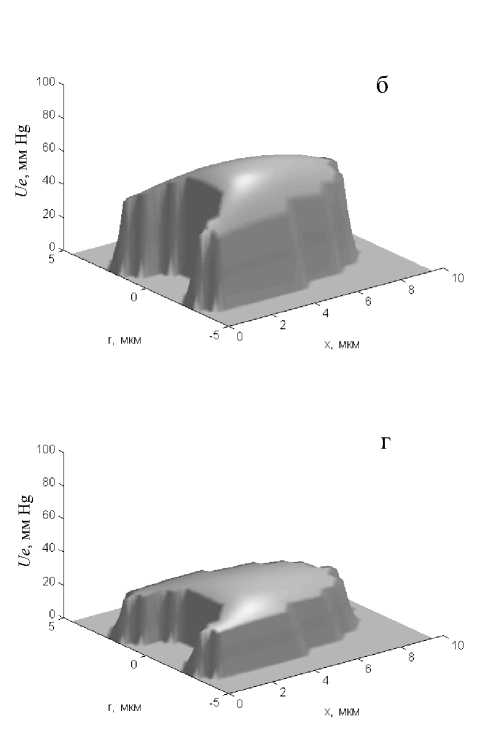
поверхности (рис. 3, в). В эритроците пулеобразной формы, аналогично, р О 2 в радиальном направлении уменьшается на 2,9 мм Hg — от 28,9 в центральной части до 26,0 мм Hg на поверхности клетки (рис. 3, г).

В отличие от распределения рО2 в цитоплазме распределение концентрации О2, связанного гемоглобином (Cg), и парциального давления рассы-щения оксигемоглобина (Ug) в эритроците остаются практически постоянными. Для эритроцита дискоидальной формы на артериальном участке капилляра в начальный момент его рассыщения (через 0,006 с) градиенты Cg и Ug в радиальном направлении от центра эритроцита к его поверхности составляют соответственно 0,0005 мл О2/мл и 0,55 мм Hg (рис. 4, а, б), а на венозном конце капилляра (через 0,6 с) — 0,0002 млО2/мл и 0,02 мм Hg (рис. 4, в, г). Еще меньшие (в 2–3 раза) градиенты этих показателей наблюдаются в эритроцитах пулеобразной формы. Однако уровни данных показателей существенно зависят от времени пребывания эритроцита в капилляре. При этом наи- большие изменения основных параметров, характеризующих транспорт О2 в капилляре (Cg, Ug, Ue), отмечаются в первые доли секунды нахождения эритроцита в капилляре. Так, через 0,1 с после начала рассыщения оксигемоглобина Cg в эритроците пулеобразной формы уменьшается от 0,47 до 0,44 мл О2/см3, Ug — от 94 до 72,1 мм Hg, а Ue — от 94 до 31,7 мм Hg. В дальнейшем наблюдается плавное уменьшение этих показателей по мере увеличения времени пребывания эритроцита в капилляре. Сходная картина наблюдается и в сегменте капилляра с эритроцитом дискообразной формы.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Динамические характеристики транспорта О2 в крови, движущейся по капилляру, исследовали с помощью математической модели, которая по сравнению с существующими имеет ряд принципиальных особенностей, позволяющих более детально имитировать реальную ситуацию. Так, во-

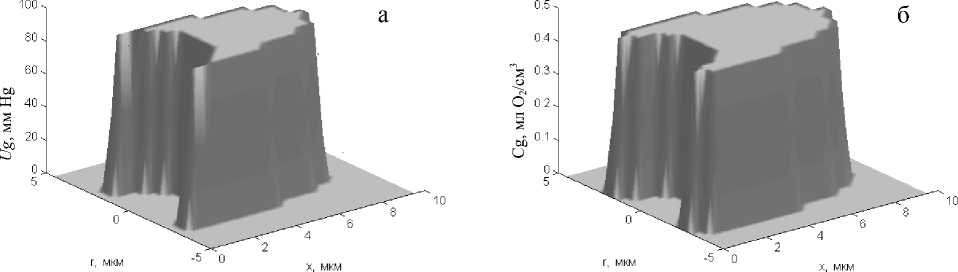
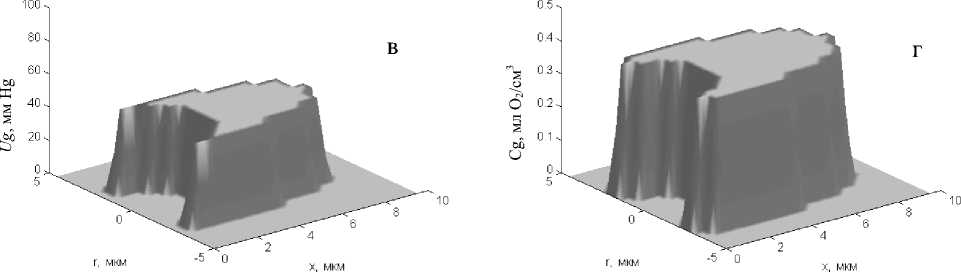
Рис. 4. Распределение парциального давления рассыщения HbO 2 (а, в) и концентрации О 2 , связанного гемоглобином (б, г), в эритроците пулеобразной формы в артериальной (а, б) и венозной (в, г) частях капилляра

первых, эритроцит в ней имеет форму, которую он обычно принимает при движении по капилляру. Во-вторых, рассматриваются процессы внутриклеточной диффузии кислорода, находящегося в растворенном и связанном оксигемоглобином состояниях. В-третьих, учтена кинетика рассыщения оксигемоглобина, которая через параметры кривой диссоциации НgО 2 связана с кислородсвязываю-щими свойствами крови. Последнее важное допущение использовалось ранее при моделировании статического распределения О 2 в эритроцитах [11]. Однако в этой модели статического распределения кислорода в отличие от настоящей модели и ее аналога [13] для характеристики кинетики рассы-щения HbO₂ вводилось сложное аналитическое выражение идеализированной кривой Хилла, что ограничивало возможности применения модели для имитации многих реальных ситуаций, связанных с изменением формы кривой диссоциации и концентрации СО 2 в крови. Исследования, выполненные на предлагаемой модели, позволили установить ряд новых принципиальных фактов, касающихся закономерностей динамики транспорта О₂ в системе микроциркуляции.

В результате выполненных расчетов удалось показать, что парциальное давление О 2 во вне- и внутриклеточном пространстве крови, движущейся по капилляру, распределено неравномерно: его наибольшие градиенты наблюдаются вблизи поверхности эритроцита. В капиллярной ячейке с эритроцитом дискоидальной формы они примерно в 1,5 раза больше, чем в ячейке с пулеобразным эритроцитом, в которой массоперенос О 2 из капилляра в окружающее пространство осуществляется более равномерно. Из этого следует, что изменения геометрической формы эритроцита под действием механических сил при движении по капилляру не только уменьшают энергозатраты на его перемещение, но и способствуют формированию равномерного стабильного поля напряжений О 2 в тканях, что имеет важное значение для адекватного потребностям обеспечения кислородом клеток с интенсивным его потреблением [15].

Существенную роль в формировании такого поля рО2 играют кислородсвязывающие свойства крови. Расчеты свидетельствуют, что в цитоплазме эритроцита вблизи его поверхности рО2 значительно ниже, чем в его центральной части (рис. 3). Это объясняется особенностью условий диффузии О2 из концентрированного его источника, каким является эритроцит, в окружающую его плазму крови. Однако в отличие от pО2 в цитоплазме уровни парциальных давлений О2, при которых осуществляется диссоциация HbO2, и концентраций связанного гемоглобином кислорода в эритроците (которые характеризуют запасы О2 в клетках крови и их способность отдавать его в окружающее пространство) в центральных и перифе- рических областях эритроцита распределены относительно равномерно. Они отличаются лишь на доли процента, что объясняется высокой скоростью диффузии HbO2 в теле эритроцита, создающей условия для «облегченной диффузии О2» [19]. За счет этого внутри эритроцита создаются достаточно высокие градиенты парциального давления в цитоплазме и давления рассыщения HbO2, что способствует стабилизации скорости отдачи им О2 в течение нескольких секунд нахождения эритроцитарной клетки в капилляре (рис. 4).

Таким образом, проведенные исследования позволили оценить особенности динамики транспорта О 2 в капилляре. Они показывают, что изменение формы эритроцита при движении его по капилляру, как и кинетические свойства процесса диссоциации оксигемоглобина и его диффузионные свойства играют важную роль в формировании стабильного и равномерного поля напряжений кислорода в тканях при постоянном кровотоке и его быстрых колебаниях. Кроме того, полученные результаты свидетельствуют о том, что в процессе движения эритроцита по капилляру осуществляются сложные взаимосвязанные процессы изменения концентраций и парциальных давлений рассыщения оксигемоглобина. Временные характеристики этих процессов значительно отличаются от характеристик изменения парциальных давлений во внеклеточном пространстве крови. Все эти обстоятельства важно учитывать при разработке технических требований к методам и техническим системам исследования процессов транспорта О₂ в системе микроциркуляции.

Автор выражает благодарность Горбенко О.М. за помощь в подготовке иллюстраций.