Математическое моделирование движения взаимодействующих частиц на основе функций распределения в плазме электродугового синтеза УНС

Открытие углеродных наноструктур (фуллеренов, нанотрубок, нановолокон) поставило задачу поиска наиболее производительного и эффективного метода их синтеза. К настоящему времени разработано значительное количество методов получения УНС, одним из которых является метод термического распыления графита в плазме электродугового разряда.

В межэлектродном промежутке графитовых стержней, находящихся в среде инертного газа (гелий, аргон), поддерживается низкотемпературный анизотропный плазменный дуговой разряд со средней энергией 0,340,43 эВ, внутри которого происходит за счет испарения перенос вещества с анода на катод.

В зависимости от режима ведения синтеза ионы углерода могут осаждаться на катоде образуя депозит, содержащий однослойные и многослойные УНТ, а могут отражаться или выбивать уже осажденные частицы из катодного депозита, формируя на стенках реакционной камеры фуллерены ряда С 60 , С 70 и т.д. с достаточно высоким выходом [1].

Определение необходимых условий и механизма образования углеродных кластеров в плазме, формирующих заданные УНС, позволит более эффективно и рационально управлять этим процессом.

Использование для математического мо- делирования данного процесса синтеза теории ионного распыления предполагает парные столкновения частиц в плазме, которые могут иметь упругий и неупругий характер. Считает- ся, что плазма состоит из электронов и однозарядных катионов углерода и буферного газа (гелия).

В основу модели, описывающей движения частиц в плазме с взаимодействием ме- жду ними, положены уравнения Власова, дополненные условием парных столкновений между частицами:

f + ^ f - qe, (E + 1^, в ]) f = o, dt    dr  me     cd df   r df   q  .-  1. r 51 _dfd

J ^с + ^_с -   (E + _[^,B])_ZR = J_£c dt     dr   mc     c       d^d dfl + ^ dfh — qL (E + 1[zy, B]) dfh J^fh dt     dr   mh     c       d^d

СТ

СТ

где fe , fc , fh - функции распределения компоненты плазмы (e - электрон, c - ион гелия, h - ион углерода); Er,Br - напряженность элек- трического и магнитного полей; qα, mα - заряд и масса частицы (α= e,c,h ); ϑr - поле скоростей частицы; rr - координаты частицы.

Допуская, что в плазме электродугового

разряда столкновения происходят только между частицами углерода и частицами буферного газа, интегралы парных столкновений запишем:

Уравнения (1) в декартовой системе координат с учетом сделанных предположений в работе [2] можно записать в виде:

∂ f с ∂ t

= ff ( ff, - ff , )i » — »'d o d»' + СТ V

∂ t

r

д Га. Z_{a F} д Г а

+    Er дГГ = Qf«, дг 2еа д»г

α

+ ff ( f ’ f ’ — ff )i = 5 — ^- d o d»',

V

где

Qf α

= K„ ^ - G.

α

∂ f _h                           ^{v r r}

-x = JJ ⁽ JhJ hx    JhJh₁ ⁾\          d ° d » +

^{∂ t} СТ V

+ JJ ( ff' — f c f )i5 — ^-' d o d » ' ,

V где f a f^ - функции распределения частиц до столкновения; f а f‘1 - после столкновения; », »' - скорости до столкновения и после

G α

д ² g ei + д» 2

д2 g„ +

д2 f ~ fα fα а -х п2 + ао +1 а ,а e,i,rt д» r     д»г

⋅

д ² g e д» 2 д ² g e

, а = e ,

, а = i ,

д 2 ghh + 1

■^^ g ^ ¹ , а = h ,

столкновения молекул соответственно; d o = 4 R 1 R ₂cos6 d Q - дифференциальное эффективное сечение рассеяния частиц в телесный угол d Q , зависящее от закона взаимодействия молекул; 0 - угол между скоростью сталкивающихся частиц и линией движения.

Начальные условия при t= 0:

fe ( ^-м = f.. f_c ( ^-м = ft Граничные условия (на аноде - А):

^{r r r}           maksv ^{r r}           maksv

^: fe ^{(r ,U},^t) -I fe     , Jc ⁽ r ^,u,^t) —I      Jc ,

А e r∈ А     e с r∈ А с fh, (r,», t)-, = f", r∈ А где fmas, fmakv, f0 - начальные распределения

С α

С α

=

=

для электронов, ионов углерода и буферного газа.   Функция распределения Максвел- fmaksv maksv :

maksv f _α

3 f -ma-15 V 2ПТ J

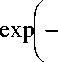
r m α _ϑ 2 n kT

2' J

где k - постоянная Больцмана; Т - температура

R α

частиц в плазме.

При переходе к безразмерным величинам используется соотношение X = M x ■ X _r ,

где M _x - масштаб размерной величины X ; X_r - безразмерная величина X . В качестве масштабов было выбрано следующие: радиус Дебая, скорость теплового движения частиц, концентрация частиц в невозмущенной плазме, потенциал, возникающий при разделении зарядов в дебаевской сфере, и производные от

K α

где

на;

них величины.

1 δ e

⋅

∂ С

—- , а = e , д » _г

⋅

δ e

1 δ e

⋅

∂ С _α ∂ ϑ _r ∂ С _α ∂ ϑ _r

, а = i ,

, а = h,

Z-(1 — Y )

-

γ

(1 - Y ) z i

(1 - Y ) Z h

4 n ^ff 1

■ f

f i

ϑ r - ϑ r ′

d » , а = e ,

■f

■f

fe ϑr - ϑr′ fe

ϑ r - ϑ r ′

-

d » , а = i ,

r d», а = h,

A

v e

■ f ^y-J + f |. f , «= i , | J.

Vn eeJ f Y f1

4 п      + f h I ■ f h , а = h ,

V V^e

4 n

T ^f- ■ ^fe , ^а = e •

V ° ^e J

ln D„           3

= —-- —, n D = ^Ml ^M n ,

^{16 п} n D Ц а

Ze = q , Z i - заряд иона, е - заряд электро-

m α

-

масса частицы сорта а ;

m _β

Y = —, в = i , h . m _e

Уравнения (1) с целью нахождения параметров электромагнитного поля были дополнены системой уравнений Максвелла, описывающих самосогласованное поле [3].

Для решение исходной системы уравнений (1) применяется модификация метода расщепления [4,5], согласно которой исходная задача разбивается на две вспомогательных. Данное разбиение можно осуществить, переписав уравнение (2) в следующем виде:

fα = Q%1 fα + Q% 2 fα , (3) ∂t где

- f г— df

Q 1 fa = — ^ ^A   +

I       d^

2 f r d ^ r V

Q^ fa = Ka 1 - Ga "f + C%a "f^ + R« ^ . ^{v2Ja a} 2 ^a Э ^²_Г^a d ^ ^a

Правая часть уравнения (3) представляет собой сумму двух операторов, первый из которых Q ~₁ f _α - отвечает за перенос частиц, второй

Q ₂ f _α - за столкновения заряженных частиц. В результате образуются следующие задачи, которые решаются последовательно:

• -    первая задача:

∂ w _α ( r , ϑ _r , t )    _%

∂tˆ      = Q1wα(r,ϑr , t), wα(r,ϑr,t)= fα(r,ϑr,tn),n=0,...N-1, fα(r,ϑr,tn)=fαmaksv,α=e,i,h,

• -    вторая задача:

∂ s ( r , ϑ , t )

^{α r}    = Q ₂ w _α ( r , ϑ _r , t ), α= e , i , h ,

∂ t

s _α ( r , ϑ _r , t_n ) = w _α ( r , ϑ _r , t_{n + 1} ), n = 0,... N - 1. (5)

Первая задача (4) представляет собой систему безразмерных уравнений Власова-Пуассона. Для ее решения применяется метод крупных частиц [6]. Вторая задача (5) решается с использованием метода сеток [5, 7].

Решением первой задачи является функция wα(r,ϑr,tn),n =0,...N, которая дает начальное условие для второй задачи. Решая вторую    задачу,    находим функцию sα(r,ϑr,tn), n =0,...N, которая определяет решение f (r,ϑ,t ),α=e,i,n исходной системы α rn для рассматриваемых моментов времени n = 1,...N,

Блок-схема алгоритма численного решения рассматриваемой задачи представлена на рис. 1.

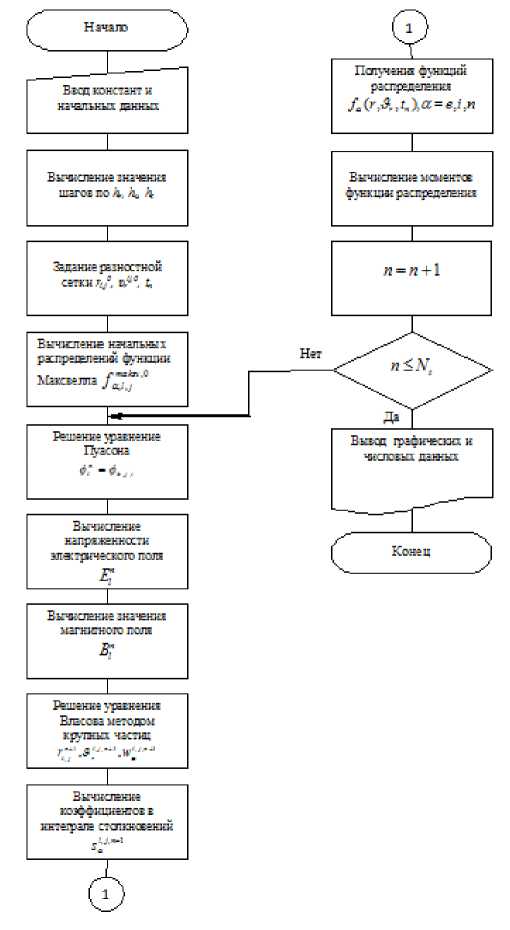
Рис.1. Алгоритм численного решения

Для реализации данного алгоритма была разработана программа «Cadpic» [8] на языке программирования Python 2.6 для операционных систем семейства GNU Linux. Разработанная программа позволяет проводить параллельные вычисления с целью сокращения времени расчета.

Пример графического представления расчета распределения скоростей ионов углерода и гелия для заданного момента времени на разных поперечных сечениях оси межэлектродного пространства представлен на рис. 2.

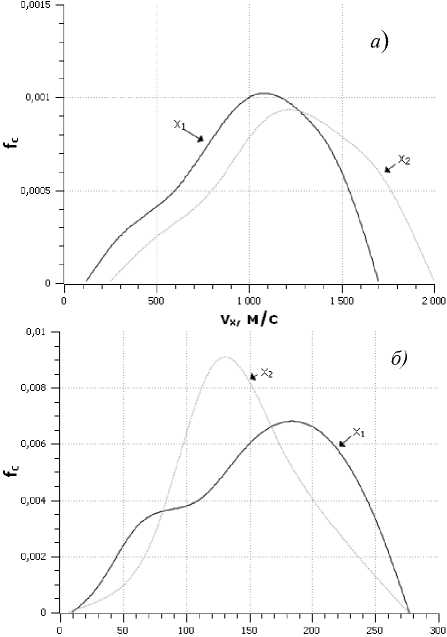
V„ м/с

Рис. 2. Функции распределения ионов углерода ( a ) и ионов гелия ( б ) в поперечном сечении оси элек-тродугового разряда при: x ₁ = 4∙10^-4 м и x ₂ =8∙10^-4 м

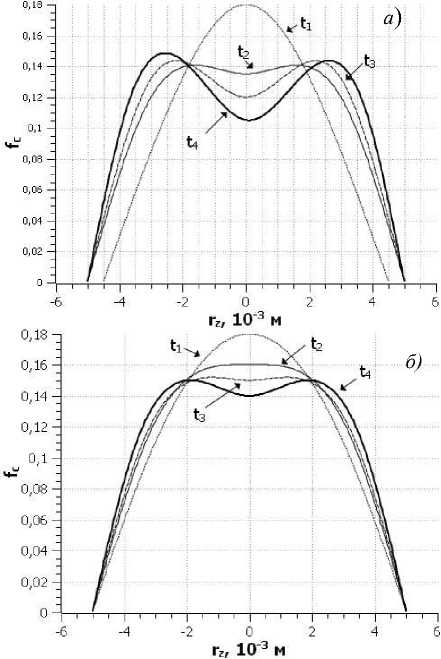
Рис. 3. Функция распределения ионов углерода в прикатодной области по радиусу электрода для режима синтеза нанотрубок (а), фуллеренов (б) и времен синтеза, с: t1 = 0,5; t2 = 1; t3 = 1,25 ; t4 = 50

Анализ приведенных зависимостей показывает, что ионы углерода в плазме имеют более высокие скорости, чем частицы гелия. При этом максимум функции распределения у частиц углерода при движении вдоль оси x смещается к максимальной скорости частиц в плазме, а у ионов гелия максимум функции распределения приходится на скорости меньше средних.

С точки зрения синтеза углеродных наноструктур наибольший интерес представляет определение зон возможного их формирования. Углеродные нанотрубки получают из катодного депозита, а фуллерены образуются в межэлектродном зазоре.

Исследование изменения функций распределения углерода в прикатодной области (рис. 3) показало, что при синтезе нанотрубок условия в начальный момент (первая секунда) могут образовываться в центре катода, а затем зона возможного формирования образуется в виде кольца с внутренним диаметром 0,4 d _эл и внешним 0,7 d эл ( d эл – диаметр электрода). При синтезе фуллеренов такого кольца не образуется.

После минуты с начала процесса зоны возможного образования наноструктур прак- тически не изменяются, и процесс является установившемся.

По функции распределения ионов углерода можно определить зоны вероятного формирования кластерных групп в плазме, образующих УНС, путем расчета концентрации ионов:

N _c ( r ^r , t ) = ∫ f _c ( r ^r , ϑ ^r , t ) d ϑ ^r ,

V где V – скорости ионов углерода, удовлетворяющие энергетическому условию образования связей между ионами углерода.

По концентрации ионов углерода можно определить зоны, в которых расстояния межу атомами достаточно для образования связи С-С или С=С, так как эти ковалентные связи отличаются длиной и энергией связи, то должно выполняться условие:

Nc(rr,t)≥ Н3 R где H – единица объема межэлектродного пространства; R – длина связи между атомами углерода.

Исследование параметров модели показало, что вероятность образования кластерных групп в плазме при синтезе фуллеренов на порядок выше, чем в режиме синтеза нанотрубок.

Анализ модели позволяет оценивать влияние таких параметров, как сила тока, давление и род буферного газа на скорость роста катодного депозита.